
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ошибок выборки. Определение необходимой численности выборки.Содержание книги
Поиск на нашем сайте
По выборочным данным производят расчет различных статистических характеристик (среднее значение, дисперсия, среднее квадратическое отклонение), значения которых затем распространяют на генеральную совокупность. Статистической оценкой или статистикой характеристики (параметра) генеральной совокупности называют приближенное значение искомой характеристики (параметра), полученное по данным выборки. В статистике используются два вида оценок - точечные и интервальные. Точечной статистической оценкой параметра генеральной совокупности называется конкретное числовое значение искомой характеристики. Интервальная оценка представляет собой числовые интервалы, предположительно содержащие значение параметра генеральной совокупности. Качество статистических оценок определяется следующими их свойствами: • Состоятельность Оценка считается состоятельной, если при неограниченном увеличении объема выборки, ее ошибка стремится к 0: • Несмещенность Оценка считается несмещенной, если при данном объеме выборки n математическое ожидание ошибки равно 0.Для несмещенной оценки ее математическое ожидание точно равно математическому ожиданию характеристики выборки • Эффективность Оценка считается эффективной, если ее ошибка, называемая ошибкой выборки, является величиной минимальной. Выборки различаются по объему единиц, в связи с чем выделяют малые и большие выборочные совокупности. Для больших выборочных совокупностей можно считать, что выборочные статистические характеристики являются не смещенными и приближенно равны статистическим характеристикам в генеральной совокупности. Для малых выборочных совокупностей (n ≤ 30) основные статистические характеристики корректируют с помощью коэффициента где
n – число вариант в выборочной совокупности. где
Такая относительная величина в генеральной совокупности носит название генеральной доли, обозначается символом Р и может быть рассчитана следующим образом: где М – число единиц генеральной совокупности, обладающих изучаемым признаком; N – число единиц в генеральной совокупности. Относительная величина изучаемого признака в выборочной совокупности называется выборочной долей, или частостью, обозначается символом W и может быть определена следующим отношением где m – число единиц выборочной совокупности, обладающих изучаемым признаком. Выборочные характеристики отличаются от статистических характеристик генеральной совокупности на определенную величину, которую называют ошибкой.. Ошибки регистрации возникают из-за неправильных или неточных сведений. Их источником является невнимательность регистратора, неправильное заполнение формуляров, описки или же непонимание существа исследуемого вопроса. Ошибки репрезентативности возникают вследствие несоответствия структуры выборки структуре генеральной совокупности. Ошибки репрезентативности делятся на систематические и случайные. Систематические ошибки репрезентативности возникают из-за неправильного формирования выборки, при котором нарушается основной принцип научно организационной выборки – принцип случайности. Случайные ошибки репрезентативности означают, что даже при соблюдении принципа случайности отбора единиц, расхождения между характеристиками выборки и генеральной совокупности все же имеют место. Предельная ошибка выборки ( где t – доверительный коэффициент, зависящий от уровня вероятности Р;
Доверительный коэффициент находится по специальной таблице, представляющей собой интегральную математическую функцию нормального распределения (приложение 1). При небольшой численности выборки распределение отличается от нормального и величина t иначе связана с вероятной оценкой, чем при большой выборке, и определяется по таблице распределения Стьюдента (приложение 2). Предельная ошибка выборки по доле рассчитывается следующим образом: где Величина средней ошибки выборки зависит от вариации признака в генеральной совокупности, объема (доли) выборки и способа отбора единиц для наблюдения. Средняя ошибка ( При бесповторном отборе средняя ошибка выборки рассчитывается следующим образом: где Средняя ошибка выборочной доли при повторном отборе рассчитывается по формуле При бесповторном отборе среднюю ошибку выборочной доли можно найти по формуле Значение средней величины в генеральной совокупности может быть представлено в виде интервальной оценки и рассчитано по данным выборочной совокупности по следующей формуле: Интервальная оценка доли рассчитывается по формуле При проектировании выборочного наблюдения решается задача нахождения необходимой численности выборки, обеспечивающей определенную точность расчета статистических характеристик генеральной совокупности. Численность выборки – один из факторов, влияющих на величину ее ошибки: чем она больше, тем меньше ошибка. С другой стороны, с объемом выборки связаны затраты на проведение исследования: чем она больше, тем больше затраты. Таким образом, выборка должна быть оптимальной по численности, чтобы обеспечить достоверность результатов исследования и не вызвать дополнительных затрат труда и денежных средств. Определяя необходимую численность выборки, надо учитывать такие факторы, как показатели вариации данного признака, величину возможной ошибки и вероятность, с которой требуется гарантировать результаты выборки. Обычно расчет необходимого объема выборки при проведении повторного отбора проводят по формуле При проведении бесповторного отбора расчет объема выборки проводят следующим образом: При определении необходимого объема выборки по выборочной доле при повторном отборе используется формула При бесповторном отборе объем выборки по выборочной доле рассчитывается следующим образом:
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.104.36 (0.009 с.) |

 , т.е. применяют точечную оценку этих характеристик
, т.е. применяют точечную оценку этих характеристик  ,
, – среднее значение признака в генеральной совокупности;
– среднее значение признака в генеральной совокупности;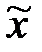 – среднее значение признака в выборочной совокупности;
– среднее значение признака в выборочной совокупности; ,
, – среднее квадратическое отклонение в генеральной совокупности;
– среднее квадратическое отклонение в генеральной совокупности; – среднее квадратическое отклонение признака по выборочной совокупности.
– среднее квадратическое отклонение признака по выборочной совокупности. ,
, ,
,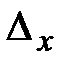 ) рассчитывается по формуле
) рассчитывается по формуле  ,
, – средняя ошибка выборки.
– средняя ошибка выборки. ,
, – средняя ошибка выборки по доле.
– средняя ошибка выборки по доле. ) случайной повторной выборки рассчитывается по формуле
) случайной повторной выборки рассчитывается по формуле  .
. ,
, – дисперсия признака выборочной совокупности.
– дисперсия признака выборочной совокупности.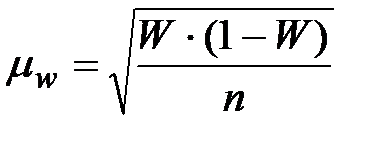
 .
. . (11)
. (11)
 .
. .
. .
. .
.


