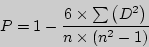Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индивидуальные и общие агрегатные индексы. Принципы их построения.
По степени охвата элементов совокупности различают индивидуальные, групповые и общие индексы. Инд-е индексы дают сравнительную хар-ку отдельных элементов той или иной совокупности (изменение объема производства какого-нибудь одного вида продукции, цен на один вид товара, урожайности одной культуры и т.д.) Инд-е индексы кол-ва какого-либо вида продукции рассчитываются: Групповые индексы (субиндексы) хар-т изм-е отдельных, обычно однородных групп (частей) сложного явления. Групп-е индексы имеют важное эк. значение. Они помогают раскрыть закономерности в изменении структуры, в развитии отдельных частей изучаемого явления. Групп-е индексы по методике расчета аналогичны общим индексам. Общие индексы хар-т изм-е всей совокупности в целом. Их можно исчислять 2 способами:1.) сначала отыскивают общие соизмерители (веса) для индексируемых величин отч. и баз. периодов, рассчитывают произведения, которые суммируют, и затем исчисляют отношение этих двух сумм.2.)сначала исчисляют индивидуальные индексы, характ-щие изм-е отдельных элементов сложного явления, а затем – среднюю величину изменений всех сопоставимых элементов. Общие индексы, исчисленные 1. способом, называются агрегатными, а 2. – средними. 32.Средние индексы: сред. Арифметические и гармонические индексы. Средние индексы рассчитывают, когда имеющаяся инф-ция не позволяет рассчитывать общий агрегатный индекс. Средний индекс – индекс, рассчитанный как сред. величина из индивид-х индексов. Сред. общие индексы получают путём преобразования агрегатных индексов. Агрегатный индекс м. б. преобразован в средний арифметический или в сред. гармонический. Форму средней нужно выбрать таким образом, чтобы полученный средний индекс был тождественен исходному агрегатному индексу. Средний ариф-й индекс тождественен агрегатному, если весами индивид-ых индексов будут слагаемые знаменателя агрегатного индекса. Средний гармонический индекс тождественен агрегатному, если веса индивидуальных индексов будут слагаемые числителя агрегатного индекса. Средний арифметический общий индекс колич-го элемента опред-ся: JV=∑ivXoVo/∑XoVo. Напр, средний арифм-й индекс физического V продукции. Он исп-ся в тех случаях, когда известны данные о стоимости продукции (обороте торговли) баз. периода и изменение кол-ва проданных товаров.Оq=∑iqp0q0/∑p0q0. Для преобразования агрегатного индекса в среднее арифметическое используютформулу инд. индекса физического V продукции. Jq=∑p0q1/∑p0q0; iq=q1/q0 à q1=iq*q0. Средний гармонический общий индекс кач-го элемента имеет вид: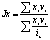 напр., средний гармонический индекс цен. Используется, когда имеются данные о стоимостипродукции отчётного напр., средний гармонический индекс цен. Используется, когда имеются данные о стоимостипродукции отчётного  периода и изменении цен на отдельные товарные группы.. Jq=∑p1q1/∑p0q1; ip=p1/p0 p1=p1/iq.33.Виды и формы взаимосвязей, изучаемых в статистике. В статистике связи классифицируются по степени их тесноты. Исходяиз этого различают функциональную (полную) и статистическую (неполную,корреляционную) связь. Функц-я связь – такая связь, при которой значение результативного признака целиком определяется значением факторного (например, площадь круга). Она полностью сохраняет свою силу и проявляется во всех случаях наблюдения идля всех единиц наблюдения. Каждому значению факторного признака соответствует одно или несколько опред-х значений результативного признака.Для корреляционной связи характерно то, что одному и тому же значению факторного признака может соответствовать сколько угодно различных значений результативного признака. Здесь связь проявляется лишь при достаточно большом кол-ве наблюдений и лишь в форме средней величины. По направлению изменений факторного и результативного признака различают связь прямую и обратную. Прямая связь – такая связь, при которой с изменением значений факторного признака в одну сторону, в ту же сторону меняется и результативный признак. Обратная связь – такая связь, при которой с увеличением (уменьшением) факторного признака происходит уменьшение (увеличение) результативногопризнака.По аналитическому выражению выделяются две основные формы связи: – прямолинейная (выражается уравнением прямой);– криволинейная (описывается уравнениями кривых линий –гипербол, парабол, степенных функций). 34.Статистические методы изучения связей. Для выявления наличия связи, её характера и направления в ст-ке используют след. методы: 1)метод сопоставления параллельных данных. При этом методе данные сопоставляются обычно в табличной форме в виде параллельно расположенных статистических рядов.Значение факторного признака располагают в возрастающем порядке, параллельно записываются значения результ-го признака и путём сопоставлении расположенных рядом рядов выявляют существование связи и её направление. На основании параллельных данных рассчитывают элементарные показатели тесноты связи: - коэффициент корреляции рангов (коэффициент Спирмена); - коэффициент совпадения знаков (коэф. Фехнера). 2) Балансовый метод. Данные взаимосвязанных показателей излагаются в виде таблиц, в которых итоги отдельных частей должны быть равны между собой. Этот метод используется для выявления взаимосвязи между видами эк. деят-ти, между производством и реализацией, для характеристики региональных связей, изучения движения ресурсных показателей (осн-х средств, ден-х средств, численности работников). Балансовая формула, хар-щая процесс движения мат. ресурсов имеет вид: Зн+П=Р+Зк. Зн, Зк – запасы ресурсов на начало и конец периода. П – поступление рес-ов в течение периода. Р– расход ресурсов. 3) Метод аналитических группировок. Чтобы осуществитьисследование связей с помощью этого метода, необходимо сгруппировать единицыизучаемой совокупности по к-л признаку и вычислить среднее значение для каждой группы. Полученные т.о ряды позволяют охарактеризовать зависимость между признаками. На базе аналит-х группировок для характ-ки тесноты связи между признаками рассчитывают эмпирическое корялиционное отношение ŋ=√δ2/δ2. 4) Графический метод. По граф. изображению связи можно определить направление, силу и форму связи. Используя данные об индивид-х значениях факторного ирезультативного признака можно построить в прямоугольных координатах точечный график, который называется поле корреляции. На оси х откладывают значения факторного признака, а на оси у – значения результативного признака. (рисунки графика)Чем сильнее связь между признаками, тем теснее будут группироваться точкивокруг определённой линии, выражающей форму связи. 35.Сущностьи виды корреляций. Основные формы корр-й связи между признаками. ермин «корреляция» в перев. означает соотношение, соответствие. К изучению связи методом корреляции обращаются в том случае, когда невозможно элиминировать (изолировать) влияние посторонних факторов либо потому, что они неизвестны, либо из-за невозможности их изоляции. Поэтому корреляционный метод применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить, какова зависимость между факторными и результатными признаками, если бы другие, посторонние факторы не изменялись и своим изменением не искажали бы основную зависимость. При этом численность выборки должна быть достаточно большой, т. к. малое число наблюдений не позволяет обнаружить закономерность связи. Повышение представительности, т.е. увеличение численности выборочной совок-ти способствует нивелированию различий между другими, неучтенными факторными признаками и, следовательно, «смягчению» их влияния на изучаемые результативные признаки. Одной из осн. задач изучения коррел-х связей является нахождение причин исследуемого явления, события, факта. При этом факторный признак выступает как причинный, а результативный –– как признак - следствие. Различают близкую к прямолинейной и криволинейную формы простой (парной) корреляционной связи. Прямолинейная простая (парная) корреляционная зависимость хар –ся возрастанием или убыванием на более-менее определенную величину результативных признаков при непрерывном возрастании факторных признаков. При прямой, близкой к прямолинейной, корреляционной связи увеличение фактора сопровождается повышением результата, при обратной – рост факторного признака вызывает снижение результативного. 36. Показатели тесноты корр-х связей: 1.)коэффициент корреляции рангов (коэффициент Спирмена) 2.) коэффициент совпадения знаков (коэф. Фехнера Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин. Величина данного коэфф. также лежит в интервале +1 и -1. Он может быть положит. и отриц-м, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале. В принципе число ранжируемых признаков (качеств, черт и т.п.) может быть любым, но сам процесс ранжирования большего, чем 20 числа признаков -- затруднителен. Ранговый коэффициент корреляции Спирмена подсчитывается по формуле: периода и изменении цен на отдельные товарные группы.. Jq=∑p1q1/∑p0q1; ip=p1/p0 p1=p1/iq.33.Виды и формы взаимосвязей, изучаемых в статистике. В статистике связи классифицируются по степени их тесноты. Исходяиз этого различают функциональную (полную) и статистическую (неполную,корреляционную) связь. Функц-я связь – такая связь, при которой значение результативного признака целиком определяется значением факторного (например, площадь круга). Она полностью сохраняет свою силу и проявляется во всех случаях наблюдения идля всех единиц наблюдения. Каждому значению факторного признака соответствует одно или несколько опред-х значений результативного признака.Для корреляционной связи характерно то, что одному и тому же значению факторного признака может соответствовать сколько угодно различных значений результативного признака. Здесь связь проявляется лишь при достаточно большом кол-ве наблюдений и лишь в форме средней величины. По направлению изменений факторного и результативного признака различают связь прямую и обратную. Прямая связь – такая связь, при которой с изменением значений факторного признака в одну сторону, в ту же сторону меняется и результативный признак. Обратная связь – такая связь, при которой с увеличением (уменьшением) факторного признака происходит уменьшение (увеличение) результативногопризнака.По аналитическому выражению выделяются две основные формы связи: – прямолинейная (выражается уравнением прямой);– криволинейная (описывается уравнениями кривых линий –гипербол, парабол, степенных функций). 34.Статистические методы изучения связей. Для выявления наличия связи, её характера и направления в ст-ке используют след. методы: 1)метод сопоставления параллельных данных. При этом методе данные сопоставляются обычно в табличной форме в виде параллельно расположенных статистических рядов.Значение факторного признака располагают в возрастающем порядке, параллельно записываются значения результ-го признака и путём сопоставлении расположенных рядом рядов выявляют существование связи и её направление. На основании параллельных данных рассчитывают элементарные показатели тесноты связи: - коэффициент корреляции рангов (коэффициент Спирмена); - коэффициент совпадения знаков (коэф. Фехнера). 2) Балансовый метод. Данные взаимосвязанных показателей излагаются в виде таблиц, в которых итоги отдельных частей должны быть равны между собой. Этот метод используется для выявления взаимосвязи между видами эк. деят-ти, между производством и реализацией, для характеристики региональных связей, изучения движения ресурсных показателей (осн-х средств, ден-х средств, численности работников). Балансовая формула, хар-щая процесс движения мат. ресурсов имеет вид: Зн+П=Р+Зк. Зн, Зк – запасы ресурсов на начало и конец периода. П – поступление рес-ов в течение периода. Р– расход ресурсов. 3) Метод аналитических группировок. Чтобы осуществитьисследование связей с помощью этого метода, необходимо сгруппировать единицыизучаемой совокупности по к-л признаку и вычислить среднее значение для каждой группы. Полученные т.о ряды позволяют охарактеризовать зависимость между признаками. На базе аналит-х группировок для характ-ки тесноты связи между признаками рассчитывают эмпирическое корялиционное отношение ŋ=√δ2/δ2. 4) Графический метод. По граф. изображению связи можно определить направление, силу и форму связи. Используя данные об индивид-х значениях факторного ирезультативного признака можно построить в прямоугольных координатах точечный график, который называется поле корреляции. На оси х откладывают значения факторного признака, а на оси у – значения результативного признака. (рисунки графика)Чем сильнее связь между признаками, тем теснее будут группироваться точкивокруг определённой линии, выражающей форму связи. 35.Сущностьи виды корреляций. Основные формы корр-й связи между признаками. ермин «корреляция» в перев. означает соотношение, соответствие. К изучению связи методом корреляции обращаются в том случае, когда невозможно элиминировать (изолировать) влияние посторонних факторов либо потому, что они неизвестны, либо из-за невозможности их изоляции. Поэтому корреляционный метод применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить, какова зависимость между факторными и результатными признаками, если бы другие, посторонние факторы не изменялись и своим изменением не искажали бы основную зависимость. При этом численность выборки должна быть достаточно большой, т. к. малое число наблюдений не позволяет обнаружить закономерность связи. Повышение представительности, т.е. увеличение численности выборочной совок-ти способствует нивелированию различий между другими, неучтенными факторными признаками и, следовательно, «смягчению» их влияния на изучаемые результативные признаки. Одной из осн. задач изучения коррел-х связей является нахождение причин исследуемого явления, события, факта. При этом факторный признак выступает как причинный, а результативный –– как признак - следствие. Различают близкую к прямолинейной и криволинейную формы простой (парной) корреляционной связи. Прямолинейная простая (парная) корреляционная зависимость хар –ся возрастанием или убыванием на более-менее определенную величину результативных признаков при непрерывном возрастании факторных признаков. При прямой, близкой к прямолинейной, корреляционной связи увеличение фактора сопровождается повышением результата, при обратной – рост факторного признака вызывает снижение результативного. 36. Показатели тесноты корр-х связей: 1.)коэффициент корреляции рангов (коэффициент Спирмена) 2.) коэффициент совпадения знаков (коэф. Фехнера Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин. Величина данного коэфф. также лежит в интервале +1 и -1. Он может быть положит. и отриц-м, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале. В принципе число ранжируемых признаков (качеств, черт и т.п.) может быть любым, но сам процесс ранжирования большего, чем 20 числа признаков -- затруднителен. Ранговый коэффициент корреляции Спирмена подсчитывается по формуле:
Σ D - сумма квадратов разностей рангов. Коэффициент Фехнера -это оценка степени согласованности направлений отклонений индивид-х значений факторного и результ-го признаков от средних значений факторного и результ-го признаков. Расчет коэффициента Фехнера состоит из следующих этапов: 1. Определяют средние значения для каждого признака (X и Y). 2. Определяют знаки отклонения (-,+) от среднего значения каждого из признаков. 3. Если знаки совпадают, присваивают значение А, иначе В.
4. Считают количество А и В, вычисляя коэффициент Фехнера по формуле: Kф = (na - nb)/(na + nb) где na - число совпадений знаков отклонений индивид-х величин от средней; nb - число несовпадений. Коэфф. Фехнера изменяется в пределах [-1;+1] и применяется для оценки тесноты связи качественных признаков (непараметрические методы). 37.Социально-экономическая статистика (СЭС) занимается количественнойхарактеристикой массовых явлений и процессов в экономике и социальной сфере. Объектом её изучения явл-ся общество во всем многообразии его форм и проявлений. СЭС является в настоящее время сложной широкоразветвленной областью знания. Она представляет собой систему научных дисциплин, основными разделами которой являются:1. Экономическая статистика – изучает явления и процессы в области экономики:стр-ру, пропорции, взаимосвязи отраслей и элементов общественного воспроизводства. В составе эк.ст-ки выделяются: макроэк-ая статистика (занимается разработкой методов комплексного изучения экономики страны, межотраслевых связей), ст-ка производственной деятельности, с/х, торговли и т.д. Задачей эк.ст-ки явл-ся разработка и анализ показателей, отраж. состояние национальной эк-ки, размещение производственных сил и использование материальных, труд. и фин. ресурсов. 2. Соц.-демографическая ст-ка изучает население, соц. явления и процессы, характеризующие условия жизнедеятельности людей. Её отраслями явл-ся: ст-ка населения; ст-ка уровня жизни и потребления мат. благ и услуг; ст-ка жилищно- коммунального хоз-ва и бытов. обслуживания населения; здравоохр-ие; наука,культура.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.152.162 (0.009 с.) |
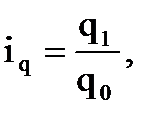 где iq – инд-ый индекс физического объема (количества) товара; q1, q2, физ. объем (количество) товара в отч. и баз. периодах.
где iq – инд-ый индекс физического объема (количества) товара; q1, q2, физ. объем (количество) товара в отч. и баз. периодах.