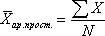Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формы, виды и способы статистического наблюдения.Содержание книги Поиск на нашем сайте Формы, виды и способы статистического наблюдения. В статистике используются 3 организационные формы наблюдения: 2. Специально организованное статистическое наблюдение – охватывает те явления, которые не получают достаточного отражения в первичном учете и отчетности, а также для дополнения и уточнения данных внутри хоз. учета. Сюда можно отнести перепись. На практике проводится перепись населения, материальных ресурсов, зеленых насаждений, незавершенных строительных объектов, оборудования и т.д. 3. Регистры – форма непрерывного статистического наблюдения за долговременными процессами по совокупности показателей. К наиболее известным относят 2 вида регистров: регистры населения и регистры предприятий. Виды стат.наблюдения: по времени- текущие, периодические, единовременные; по полноте охвата совокупности – сплошное, несплошное(выборочное, монографическое, обследование основного массива). Способы стат. наблюдения: · непосредственно наблюдение; · Документируемое наблюдение; · Опрос(экспедиционный,саморегистрации,анкетный,корреспондентский). Ошибки наблюдения. Точность и достоверность данных является наиболее важным требованием статистики. Точностью считается мера соответствия данных наблюдения действительной их величине, достоверностью – мера объективного отображения ими сущности явлений и процессов. Различают ошибки регистрации и репрезентативности. Систематические ошибки приводят к значительным отклонениям общих результатов наблюдений. Они бывают преднамеренные и непреднамеренные (например, непреднамеренной является ошибка, связанная с тенденцией округлять свой возраст людьми старшего поколения, преднамеренные ошибки часто встречаются при составлении отчетности предприятий). Логический контроль обычно состоит в сопоставлении ответов на взаимосвязанные вопросы, что позволяет выявить несовместимость ответов. Арифметический контроль заключается в проверке всех обобщающих показателей и в согласовании тех показателей, которые выводятся один из другого.
9.Нормативно-правовая база стат. учета пожаров и их последствий: · Конституция РФ; · №282ФЗ «Об офиц.стат. учете и системе Гос. Статистики в РФ»; · №69 ФЗ «О пожарной безопасности»; · Постановления правительства №290 «О федер. Гос. Пож. Надзоре»; · Приказ МЧС России от 21.11.08. №714 «об утверждении Порядка учета пожаров и их последствий»; · Приказ МЧС России №760 «О формировании электронных баз данных учета пожаров и их последствий»; · Приказ ФСГС №311 «Об утверждении статистического инструментария для организации МЧС России федерального статистического наблюдения за пожарами и последствиями от них». Основные положения офиц. Стат. учета пожаров и их последствий. 3. Официальный статистический учет пожаров и их последствий представляет собой деятельность, направленную на проведение федерального статистического наблюдения по пожарам и их последствиям и обработке данных, полученных в результате этих наблюдений. 4. Федеральное статистическое наблюдение по пожарам и их последствиям включает в себя сбор первичных статистических данных по пожарам и их последствиям и административных данных по пожарам (загораниям) и их последствиям. 5. Первичные статистические данные по пожарам и их последствиям содержат документированную информацию по формам федерального статистического наблюдения по пожарам, получаемую от респондентов. 6. Административные данные по пожарам (загораниям) и их последствиям содержат документированную информацию по формам учета пожаров (загораний) и их последствий и (или) электронных баз данных учета пожаров (загораний) и их последствий, устанавливаемым респондентами, обеспечивающим возможность формирования официальной статистической информации. 7. Федеральное статистическое наблюдение по пожарам и их последствиям является сплошным и проводится в отношении респондентов, к которым относятся созданные на территории Российской Федерации юридические лица, федеральные органы исполнительной власти, граждане Российской Федерации, находящиеся на территории Российской Федерации иностранные граждане и лица без гражданства, граждане, осуществляющие предпринимательскую деятельность без образования юридического лица на территории Российской Федерации. 8. Федеральное статистическое наблюдение по пожарам и их последствиям осуществляется по формам-образцам статистических документов, предназначенным для получения от респондентов в установленном порядке первичных статистических данных по пожарам и их последствиям, в соответствии с указаниями по их заполнению, утверждаемыми уполномоченным Правительством Российской Федерации федеральным органом исполнительной власти по представлению субъекта официального статистического учета пожаров и их последствий*(5). 9. Официальная статистическая информация по пожарам и их последствиям формируется субъектом официального статистического учета пожаров и является сводной документированной информацией о количественной стороне происшедших пожаров. 10. Субъектом официального статистического учета пожаров и их последствий является федеральный орган исполнительной власти, осуществляющий формирование официальной статистической информации по пожарам и их последствиям в соответствии с законодательством Российской Федерации. 11. Установленный порядок учета пожаров и их последствий обязателен для исполнения органами государственной власти, органами местного самоуправления, организациями и гражданами, осуществляющими предпринимательскую деятельность без образования юридического лица*(6). 12. Официальная статистическая информация по пожарам и их последствиям является общедоступной, за исключением информации, доступ к которой ограничен федеральными законами. Обеспечение доступа заинтересованных пользователей к общедоступной официальной статистической информации по пожарам и их последствиям осуществляется путем ее распространения или предоставления субъектом официального статистического учета пожаров и их последствий в соответствии с законодательством Российской Федерации.
Порядок учета пожаров 13. Официальному статистическому учету подлежат все пожары, для ликвидации которых привлекались подразделения пожарной охраны, а также пожары, в ликвидации которых подразделения пожарной охраны не участвовали, но информация о которых поступила от граждан и юридических лиц. 14. Не подлежат официальному статистическому учету: 1) случаи горения, предусмотренные технологическим регламентом или иной технической документацией, а также условиями работы промышленных установок и агрегатов; 2) случаи горения, возникающие в результате обработки предметов огнем, теплом или иным термическим (тепловым) воздействием с целью их переработки, изменения других качественных характеристик (сушка, варка, глажение, копчение, жаренье, плавление и др.); 3) случаи задымления при неисправности бытовых электроприборов и приготовлении пищи без последующего горения; 4) случаи взрывов, вспышек и разрядов статического электричества без последующего горения; 5) случаи коротких замыканий электросетей, в электрооборудовании, бытовых и промышленных электроприборах без последующего горения; 6) пожары, происшедшие на объектах, пользующихся правом экстерриториальности; 7) случаи горения автотранспортных средств, причиной которых явилось дорожно-транспортное происшествие; 8) пожары, причиной которых явились авиационные и железнодорожные катастрофы, форс-мажорные обстоятельства (террористические акты, военные действия, спецоперации правоохранительных органов, землетрясения, извержение вулканов и др.); 9) покушения на самоубийство и самоубийства путем самосожжения, не приведшие к гибели и травмированию других людей либо уничтожению, повреждению материальных ценностей; 10) случаи неконтролируемого горения, не причинившие материальный ущерб, вред жизни и здоровью граждан, интересам общества и государства (далее - загорания). Как загорания учитываются следующие случаи горения (независимо от причин его возникновения), не приведшие к его распространению на иные объекты защиты: бесхозных зданий; бесхозных транспортных средств; сухой травы; тополиного пуха; торфа на газонах и приусадебных участках; пожнивных остатков; стерни; мусора на свалках, пустырях, на территории домовладений, на обочинах дорог, на контейнерных площадках для его сбора, в контейнерах (урнах) для его сбора, в лифтовых шахтах (лифтах) жилых домов, в мусоросборниках (мусоропроводах) жилых домов, на лестничных клетках жилых домов, в подвальных и чердачных помещениях жилых домов.
Сводка. В результате статистического наблюдения собирают сведения о каждой единице наблюдения, т.е. исходный материал. Дальнейшая задача состоит в приведении этого материала в определенный порядок. Она решается с помощью сводки. Сводка в узком смысле слова — это подсчет итогов в группах и подгруппах и оформление этого материала в таблицы. Этапы сводки: 1) группировка полученных при наблюдении данных; Программа сводки в общем виде содержит перечень групп, на которые нужно распределить совокупность, а также перечень показателей, используемых для характеристики совокупности в целом, ее отдельных частей. План сводки — это этапы ее последовательности, сроки выполнения отдельных частей сводки, исполнители и порядок изложения результатов сводки.
Группировки, их виды. Группировка — это метод, который позволяет распределить совокупность на группы по признакам сходства или различия. Одним из важнейших этапов группировки является выбор группировочного признака, потому что от этого зависят результаты сводки и группировки в целом. Выбор признаков в каждом конкретном случае должен основываться на экономической сущности изучаемого явления, на основе тщательного анализа. С помощью метода группировки решаются следующие важнейшие задачи: Существуют несколько различных классификаций группировок. В зависимости от количества группировочных признаков выделяют: 2) комбинационные группировки — это распределение совокупности по двум-трем признакам, взятым в комбинации друг с другом. В этой группировке группы, образованные по одному признаку, разделяются на подгруппы по другому признаку. В зависимости от характера группировочного признака различают: 2) количественные группировки — в их основе лежит количественный признак, выражающийся числом. В зависимости от характера статистических данных различают: 2) вторичные группировки - это группировки, построенные на основе данных других группировок, т.е. это образование новых трупп на основе ранее проведенной группировки.
Многомерные группировки.
Многочисленные методы многомерной группировки (кластер-анализа) несмотря на имеющиеся различия вычислительных процедур, реализуются при последовательном выполнении общих алгоритмических шагов: - формирование матрицы исходных данных (X) размере nх т, где п - число объектов наблюдения, т - число признаков, по которым производится группировка; - переход от матрицы исходных данных к матрице нормированных данных (Z). Решение этой задачи означает, что разнородные по своей физической природе признаки приводятся к одному основанию, имеют одну и ту же условную единицу измерения. Переход осуществляется пересчетом значений группировочных признаков (хij) в zijпо одному из следующих вариантов:
Zij = Xij / Xj (эталон), (10.2) Zij =Xij/Xjмах, (10.3) Zij= Xij/Xjмах, (10.4) Zij= (Xij - Xj)/(Xj мах- Xj мin). (10.5) - определение расстояний между всеми парами наблюдаемых объектов (d ij ) и построение исходной матрицы расстояний (D0); Для определения расстояний между объектами наблюдения, представляемых в теоретическом пространстве, существует набор метрик. Выбор метрики осуществляется самим исследователем. С целью определения расстояний между объектами наблюдения кроме метрик расстояний могут использоваться и статистические меры сходства, как, например, коэффициенты парной корреляции, коэффициенты конкордации и т. д.; - производится выбор конкретной процедуры кластер-анализа и по данным исходной матрицы расстояний (D0) последовательно выделяются группы однородных объектов. В настоящее время имеется достаточно большое количество различных процедур кластеризации данных, они объединяются в шесть основных семейств: - итеративные методы группировки; - методы поиска модальных значений плотности; - факторные методы; - методы поиска сгущений; - методы, использующие теорию графов. При помощи конкретного, отобранного заранее метода кластер-анализа выполняются вычислительные процедуры и получают разделение совокупности на кластеры (классы, группы): Перечисленных шагов может быть достаточно, если анализируются обычные признаки, имеющие количественную определенность. Если же в анализе участвуют ранговые (порядковые) или другие качественные характеристики, то приведенному выше алгоритму предшествуют этапы оцифровки неколичественных данных. Из большого числа методов многомерной группировки в настоящее время наиболее широкое распространение получил иерархический кластерный анализ. Он может быть агломеративным и дивизимным. В агломеративном кластер-анализе вначале каждый объект рассматривается как отдельный кластер, в последующем происходит их объединение до тех пор, пока все объекты не окажутся в одном кластере. В дивизимном кластер-анализе, наоборот, вначале вся совокупность объектов наблюдения — это один кластер, затем в ходе разделения совокупности приходят к состоянию, когда каждый объект рассматривается как отдельный кластер. Однородные группы в иерархическом кластер-анализе определяются после графического представления результатов кластеризации в виде особенного графика — дендограммы. Абсолютные величины. Первичная статистическая информация выражается прежде всего в виде абсолютных показателей, которые являются количественной базой всех форм учета. Абсолютные показатели характеризуют итоговую численность единиц совокупности или ее частей, размеры (объемы, уровни) изучаемых явлений и процессов, выражают временные характеристики. Абсолютные показатели могут быть только именованными числами, где единица измерения выражается в конкретных цифрах. В зависимости от сущности исследуемого явления и поставленных задач единицы измерения могут быть натуральными (физические меры массы, длины, объема), условно-натуральными (например, молочные продукты с разным содержанием сливочной основы, мыло с разным содержанием жирных кислот и т.д.), стоимостными (денежное выражение) и трудовыми (затраты труда, трудоемкость технологических операций в человеко-днях, человеко-часах). Вся совокупность абсолютных величин включает как индивидуальные показатели (характеризуют значения отдельных единиц совокупности), так и суммарные показатели (характеризуют итоговое значение нескольких единиц совокупности или итоговое значение существенного признака по той или иной части совокупности). Абсолютные показатели следует также подразделить на моментные и интервальные.
Относительные величины — это отвлеченные статистические величины, выражающие количественное соотношение двух величин. Относительные величины измеряются в коэффициентах, процентах, промилях, комплексных единицах. Видыотносительныхвеличин:
ОВД =(У1 /У0 )х100%. Относительные величины динамики характеризуют изменение явления во времени. В статистике эти показатели называются темпами роста; 2) относительные величины выполнения плана- ОВВП =(У1 /Уплан)х 100%. Эта относительная величина показывает степень выполнения плана в процентах; 3) относительная величина выполнения планового задания ОВПЗ=(Уплан /У0)х 100%. Показывает, на сколько процентов плановое задание выше (ниже) фактически достигнутого в базисном периоде.Эту величину называют плановым темпом роста; 4) относительная величина структуры 7) относительная величина сравнения — это отношение одноименных величин, характеризующих разные объекты изучения за один и тот же период. Показывает, во сколько разчислитель больше (меньше) знаменателя.
27. Средняя арифметическая,способы ее расчета. Средняя гармоническая.
где X - значения величин, для которых необходимо рассчитать среднее значение; N - общее количество значений X (число единиц в изучаемой совокупности). Средняя арифметическая взвешенная имеет следующий вид:
где f - количество величин с одинаковым значением X (частота). Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X остутствует нижнияя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X. Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Б) Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Например, автомобиль ехал из пункта А в пункт Б со скоростью 90 км/ч, а обратно - со скоростью 110 км/ч. Для определения средней скорости применим формулу средней гармонической простой, так как в примере дано расстояние w1=w2 (расстояние из пункта А в пункт Б такое, же как и из Б в А), которое равно произведению скорости (X) на время (f). Средняя скорость = (1+1)/(1/90+1/110) = 99 км/ч. Средняя геометрическая и средняя хронологическая. А) Средняя геометрическая применяется при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
28. Мода и медиана:понятие,принципы расчета и графического определния.
где Мо – мода; ХНМо – нижняя граница модального интервала; hМо – размах модального интервала (разность между его верхней и нижней границей); fМо – частота модальноого интервала; Б) Статистическая медиана – это значение величины X, которое делит упорядоченную по возрастанию или убыванию статистическую совокупность на 2 равных по численности части. В итоге у одной половины значение больше медианы, а у другой - меньше медианы. Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана; ХНМе – нижняя граница медианного интервала; hМе – размах медианного интервала (разность между его верхней и нижней границей); fМе – частота медианного интервала; fМе-1 – сумма частот интервалов, предшествующих медианному. 29. Понятие вариации, ее значение. Вариацию можно определить как количественное различие значений одного и того же признака у отдельных единиц совокупности. К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию. Связи. В статистике связи классифицируются по степени их тесноты. Исходя из этого различают функциональную (полную) и статистическую (неполную, корреляционную) связь. Функциональная связь – такая связь, при которой значение результативного признака целиком определяется значением факторного (например, площадь круга определяется величиной радиуса).Она полностью сохраняет свою силу и проявляется во всех случаях наблюдения и для всех единиц наблюдения. Каждому значению факторного признака соответствует одно или несколько определенных значений результативного признака. Для корреляционной связи характерно то, что одному и тому же значению факторного признака может соответствовать сколько угодно различных значений результативного признака. Здесь связь проявляется лишь при достаточно большом количестве наблюдений и лишь в форме средней величины. По направлению изменений факторного и результативного признака различают связь прямую и обратную. Прямая связь – такая связь, при которой с изменением значений факторного признака в одну сторону, в ту же сторону меняется и результативный признак. Обратная связь – такая связь, при которой с увеличением (уменьшением) факторного признака происходит уменьшение (увеличение) результативного признака.
По аналитическому выражению выделяются две основные формы связи: – прямолинейная (выражается уравнением прямой); – криволинейная (описывается уравнениями кривых линий – гипербол, парабол, степенных функций). Кроме того связи могут быть однофакторными (результативная переменная зависит от одного фактора или переменной) и многофакторными (результативная переменная зависит от нескольких факторов взятых в комбинации). 36. Понятие корреляционной связи Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, может ли рост влиять на вес человека или может ли давление влиять на качество продукции? Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь - это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого. Известно, например, что в среднем между ростом людей и их весом наблюдается положительная связь, и такая, что чем больше рост, тем больше вес человека. Однако из этого правила имеются исключения, когда относительно низкие люди имеют избыточный вес, и, наоборот, астеники, при высоком росте имеют малый вес. Причиной подобных исключений является то, что каждый биологический, физиологический или психологический признак определяется воздействием многих факторов: средовых, генетических, социальных, экологических и т.д. Корреляционные связи - это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статистики. Оба термина - корреляционная связь и корреляционная зависимость - часто используются как синонимы. Зависимость подразумевает влияние, связь - любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого. Корреляционная зависимость - это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака. Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции. Корреляционные связи различаютсяпо форме, направлению и степени (силе). По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. Криволинейной может быть, например, связь между уровнем мотивации и эффективностью выполнения задачи (рисунок 1). При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности.
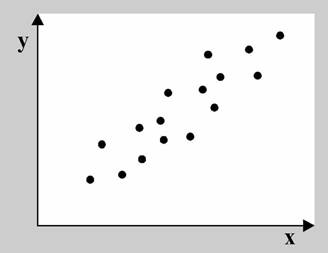
Рисунок 1 - Связь между эффективностью решения задачи и силой мотивационной тенденции По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). При положительной прямолинейной корреляции более высоким значениям одного признака соответствуют более высокие значения другого, а более низким значениям одного признака - низкие значения другого (рисунок 2). При отрицательной корреляции соотношения обратные (рисунок 3). При положительной корреляции коэффициент корреляции имеет положительный знак, при отрицательной корреляции - отрицательный знак[1].
Рисунок 2 – Прямая корреляция
Рисунок 3 – Обратная корреляция
Рисунок 4 – Отсутствие корреляции Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.
39. Динамические ряды: понятие и их характеристика. Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени (годы, кварталы, месяцы, дни или даты); 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.
40.Индивидуальные показатели рядов динамики. < |
|||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |


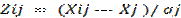 (10.1)
(10.1) Моментные абсолютные показатели характеризуют факт наличия явления или процесса, его размер (объем) на определенную дату времени.
Моментные абсолютные показатели характеризуют факт наличия явления или процесса, его размер (объем) на определенную дату времени.