
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принципы построения группировокСодержание книги Поиск на нашем сайте
Для построения статистических группировок нужно выбрать группировочный признак, далее определить количество групп, на которые разбивают изучаемую статистическую совокупность и зафиксировать границы интервалов группировки. Для каждой группировки нужно находить конкретные показатели или их систему, которые должны охарактеризовать изучаемые группы. Выбор группировочного признака – сложный вопрос в теории статистической группировки и статистического исследования в целом. Группировочный признак – это основание, по которому проводится разбивка единиц совокупности на отдельные группы. От степени точности группировочного признака зависит правильность выводов статистического исследования. В группировку входят количественные и атрибутивные (качественные) признаки. Количественные признаки обычно имеют числовое выражение (например, объем выпускаемой продукции, возраст человека, доход семьи и т. д.). Атрибутивные признаки дают качественную характеристику единицы совокупности (например, пол, семейное положение, политическая ориентация человека и т. д.). Выделенные группы по атрибутивному признаку в группировке должны отличаться друг от друга по качественной характеристике признака. Число групп, на которые расчленяется статистическая совокупность, зависит от количества градаций атрибутивного признака. Важно изучить экономическую сущность исследуемого явления при построении группировки по количественному признаку. Для определения числа групп можно воспользоваться формулой Стерджесса: h + 3,322? lg N, где h – число групп; N – число единиц совокупности; lgN – десятичный логарифм от N. Данная формула говорит о том, что выбор числа групп объектно зависит от объема совокупности. После установления числа групп решается вопрос об определении интервалов группировки. На основе интервала группировки можно количественно различить одни группы от других и наметить границы выделения их нового качества. Интервал группировки – это интервал значений варьирующего признака, лежащих в пределах определенной группы. Каждый интервал имеет свою длину (ширину), верхнюю и нижнюю границы. Нижняя граница интервала – это наименьшее значение признака в интервале, а верхняя граница интервала – его наибольшее значение. За нижнюю границу первого интервала принимают наименьшее значение признака в совокупности единиц наблюдения. Верхняя граница последнего интервала не может быть меньше наибольшего значения признака в совокупности единиц наблюдения. Ширина интервала – это разность между верхней и нижней границами. Интервалы группировки в зависимости от их ширины бывают равными и неравными. Неравные делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные. Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами. Величина равного интервала определяется по следующей формуле: h = R/n = (х мах – х min) / n, гдех мах,х min – максимальное и минимальное значение признака в совокупности; n – число групп.Данную формулу называют шагом интервала. Если размах вариации признака в совокупности велик и значения признака варьируются неравномерно, то используют группировку с неравными интервалами. Неравные интервалы могут быть получены, если построенная группировка с равными интервалами содержит группы, не отражающие определенные типы изучаемого явления или процесса или не содержащие ни одной единицы совокупности, возникает необходимость увеличения – объединения двух или нескольких малочисленных или «пустых» последовательных равных интервалов. Выбор равных или неравных интервалов зависит от степени заполнения интервалов. Интервалы группировок могут быть закрытыми и открытыми Закрытыми интервалами являются интервалы, в которых указаны верхняя и нижняя границы. Открытые интервалы имеют только одну границу (верхнюю – у первого, нижнюю – у последнего). К количественным признакам можно отнести непрерывный признак, или дискретный. Если в основании группировки лежит дискретный признак, то нижняя граница i – го интервала равна верхней границе i – го интервала, увеличенной на 1. В группировках, отражающих качественные особенности и специфику выделяемых групп единиц изучаемой совокупности по определенному признаку, применяются специализированные интервалы. Специализированные интервалы – это интервалы, которые применяются для выделения из совокупности одних и тех же типов по одному и тому же признаку у явлений, находящихся в различных условиях. По роли, которую играют признаки во взаимосвязи изучаемых объектов, процессов или явлений, их можно подразделить на факторные и результативные. Факторные признаки воздействуют на другие признаки, а результативные испытывают на себе влияние других признаков. Многомерные группировки.
Многочисленные методы многомерной группировки (кластер-анализа) несмотря на имеющиеся различия вычислительных процедур, реализуются при последовательном выполнении общих алгоритмических шагов: - формирование матрицы исходных данных (X) размере nх т, где п - число объектов наблюдения, т - число признаков, по которым производится группировка; - переход от матрицы исходных данных к матрице нормированных данных (Z). Решение этой задачи означает, что разнородные по своей физической природе признаки приводятся к одному основанию, имеют одну и ту же условную единицу измерения. Переход осуществляется пересчетом значений группировочных признаков (хij) в zijпо одному из следующих вариантов:
Zij = Xij / Xj (эталон), (10.2) Zij =Xij/Xjмах, (10.3) Zij= Xij/Xjмах, (10.4) Zij= (Xij - Xj)/(Xj мах- Xj мin). (10.5) - определение расстояний между всеми парами наблюдаемых объектов (d ij ) и построение исходной матрицы расстояний (D0); Для определения расстояний между объектами наблюдения, представляемых в теоретическом пространстве, существует набор метрик. Выбор метрики осуществляется самим исследователем. С целью определения расстояний между объектами наблюдения кроме метрик расстояний могут использоваться и статистические меры сходства, как, например, коэффициенты парной корреляции, коэффициенты конкордации и т. д.; - производится выбор конкретной процедуры кластер-анализа и по данным исходной матрицы расстояний (D0) последовательно выделяются группы однородных объектов. В настоящее время имеется достаточно большое количество различных процедур кластеризации данных, они объединяются в шесть основных семейств: - итеративные методы группировки; - методы поиска модальных значений плотности; - факторные методы; - методы поиска сгущений; - методы, использующие теорию графов. При помощи конкретного, отобранного заранее метода кластер-анализа выполняются вычислительные процедуры и получают разделение совокупности на кластеры (классы, группы): Перечисленных шагов может быть достаточно, если анализируются обычные признаки, имеющие количественную определенность. Если же в анализе участвуют ранговые (порядковые) или другие качественные характеристики, то приведенному выше алгоритму предшествуют этапы оцифровки неколичественных данных. Из большого числа методов многомерной группировки в настоящее время наиболее широкое распространение получил иерархический кластерный анализ. Он может быть агломеративным и дивизимным. В агломеративном кластер-анализе вначале каждый объект рассматривается как отдельный кластер, в последующем происходит их объединение до тех пор, пока все объекты не окажутся в одном кластере. В дивизимном кластер-анализе, наоборот, вначале вся совокупность объектов наблюдения — это один кластер, затем в ходе разделения совокупности приходят к состоянию, когда каждый объект рассматривается как отдельный кластер. Однородные группы в иерархическом кластер-анализе определяются после графического представления результатов кластеризации в виде особенного графика — дендограммы.
|
|||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.20.108 (0.009 с.) |


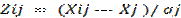 (10.1)
(10.1)


