Дайте понятие средней величины

Средняя величина – это обобщающая количественная характеристика качественно-однородной совокупности по варьирующему признаку.

Как рассчитать среднюю арифметическую простую, взвешенную величины?

средняя арифметическая простая. Она применяется, если известны все значения вариант-признака

– средняя арифметическая взвешенная. Применяется, если данные сгруппированы и это выражается частотами

32.Назовите этапы расчета средней арифметической из вариационного ряда спо­собом моментов.

1.Из всех вариантов Xi вычесть одно и то же постоянное число а (обычно им является либо середина ряда, либо вариант с наибольшей частотой)

2.все варианты необходимо разделить на постоянное число К-интервал

3.Сосчитать промежуточную варианту

4.Вычислить величину Xi*Fi

5.Определяем момент первого порядка

6.

Какова область применения средней гармонической величины?

Средняя арифметическая, как было показано выше, применяется в тех случаях, когда известны варианты варьирующего признака х и их частоты f.

В чем заключается правило мажорантности средних?

Правило можарантности средних: значение средней величины увеличивается при возрастании степени Z.

Приведите основные свойства средних величин.

1.произведение средней величины на сумму частот равно сумме произведений отдельных вариант на частоту

X Efi=E XiFi

2.Если от каждой варианты отнять (прибавить) какое-либо произведение числа а, то средняя соответственно уменьшится (увеличится) на это число а

3.Если каждую варианту умножить (разделить) на какое-то число К, то средняя соответственно увеличится (уменьшится) на столько же раз

Дайте понятие логической формулы средней величины.

Это словесное описание определяемой величины. Отношение суммы значения признака к численности совокупности

Что характеризуют структурные средние?

Структурные средние характеризуют структуру рядов распределения.

Как определить моду и медиану в интервальном ряду?

 

Xmo- нижняя граница модального интервала

i-интервал

Fmo- модальная частота

 

Где используются структурные средние?

применяется для изучения внутреннего строения рядов распре­деления значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен.

Каковы сущность и значение показателей вариации?

Показатели вариации определяют как группируются значения признака вокруг средней величины. Они используются для характеристики упорядоченных статистических совокупностей: группировок, классификаций, рядов распределения. В наибольшей степени вариации подвержены курсы акций, объёмы спроса и предложения, процентные ставки в разные периоды и в разных местах.

Что представляет собой вариация признака, от чего зависят ее размеры?

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака

Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае.

Назовите показатели, характеризующие степень отклонения признака от центра распределения.

Средняя арифметическая, мода, медиана

Какой показатель характеризует степень однородности совокупности по изучаемому признаку?

Коэффициент вариации

В чем недостатки показателя размаха вариации?

Размах вариации не показывает как ведут себя варианты в рядах распределения

Как определить среднее линейное отклонение?

Среднее линейное отклонение – это среднее отклонение варианты от средней величины ряда.

– для сгруппированных данных

 

- для не сгруппированных данных

 

В чем недостаток линейных показателей вариации?

Основным недостатком этого показателя является то, что он определяется двумя крайними значениями, в то время как вариация признака складывается из всех его значений.

 

Как вычисляется дисперсия?

- для сгруппированных данных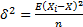

 

– для не сгруппированных данных