
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление рядов динамики при определении гармоник ФурьеСодержание книги
Поиск на нашем сайте
Для расчета гармоники используется вспомогательная таблица, которая для первой гармоники имеет следующий вид (табл. 8.6). Таблица 8.6 Вспомогательная таблица для расчета первой гармоники (к=1)
Таким образом, для вычисления синусов и косинусов разных гармоник ( Таблица 8.7 Значения синусов и косинусов для гармоник Фурье
В результате по полученным параметрам строится математическая модель, на основе которой определяются расчетные уровни Анализ рядов динамики и прогнозирование Анализ рядов динамики социально-экономических явлений, выявление тренда и сезонной волны, служат основой для прогнозирования в экономике. Прогнозирование – это оценка будущего состояния социально – экономических явлений на основе анализа тенденций их развития. Составление надежных прогнозов динамики спроса и предложения туристского рынка является необходимым условием рыночной конкуренции. Статистическое прогнозирование основано на анализе рядов динамики, и состоит из трех этапов: § обобщение данных, собранных за длительный период; § выявление статистической закономерности; § распространение закономерностей на будущее. Ведущую роль в прогнозировании играют статистические методы экстраполяции. Под экстраполяцией понимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее. Другими словами, экстраполяция – это определение уровней за пределами динамического ряда. При этом экстраполяция, проводимая в будущее, называется перспективой, а в прошлое - ретроспективой. Тенденция развития может изменяться, поэтому данные, полученные путем экстраполяции ряда, следует рассматривать в качестве оценочных, вероятностных. Любое прогнозирование основано на предположении, что закономерность, действующая внутри анализируемого ряда динамики, сохранится и в дальнейшем. В этой связи при экстраполяции большое значение имеют продолжительность базисного ряда динамики и сроки прогнозирования. Следует иметь в виду, что чем короче сроки прогноза, тем надежнее результаты экстраполяции. Перечислим некоторые простейшие методы экстраполяции. Метод среднего абсолютного прироста. Если при анализе ряда динамики обнаруживается, что абсолютные приросты уровней примерно постоянны (
где Применение этого метода предполагает, что развитие явления происходит по арифметической прогрессии. Метод относится к классу «наивных» моделей, так как чаще всего развитие явления отличается арифметической прогрессии. Однако в ряде случаев этот метод может использоваться в качестве предварительного прогноза. Например, если у исследователя нет динамического ряда, а есть лишь информация на начало и конец периода (например, данные баланса). Метод среднего темпа роста. Если за исследуемый период стабильны темпы роста (
Указанные методы экстраполяции имеют следующий недостаток: они учитывают лишь начальный и конечный уровень ряда, исключая промежуточные уровни. Однако они могут быть использованы в качестве приближенных оценок, предшествующих более глубокому анализу.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.67.90 (0.006 с.) |

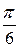
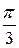
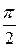
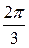
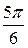
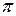

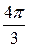

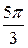
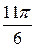
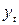

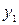
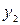
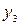

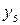
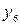
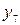
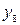
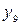
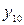
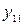
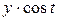

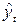
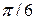
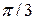

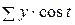


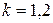 ) используют данные табл. 8.7.
) используют данные табл. 8.7.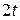

 const), то необходимо определить средний абсолютный прирост
const), то необходимо определить средний абсолютный прирост 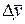 . Затем последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд. Расчеты ведутся по формуле:
. Затем последовательно прибавить его к последнему уровню ряда столько раз, на сколько периодов экстраполируется ряд. Расчеты ведутся по формуле: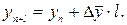
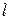 - срок прогноза;
- срок прогноза;  - экстраполируемый уровень;
- экстраполируемый уровень; 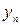 - конечный уровень ряда;
- конечный уровень ряда; 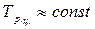 ), то необходимо рассчитать средний темп роста
), то необходимо рассчитать средний темп роста 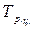 . Затем следует умножить последний уровень ряда на средний темп роста
. Затем следует умножить последний уровень ряда на средний темп роста 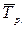 в степени, соответствующей периоду экстраполяции. Расчет ведется по формуле:
в степени, соответствующей периоду экстраполяции. Расчет ведется по формуле: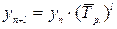 .
.


