Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для расчета коэффициента взаимной сопряженностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Величину
Рассмотрим модификацию коэффициента Пирсона на основе расчета
где Рассмотрим модификацию коэффициента сопряженности Чупрова. В этом случае применяется формула вида:
где Для оценки связи между качественным альтернативным и количественным варьирующим признаками применяется биссериальный коэффициент корреляции:
где Ранговые коэффициенты связи
Методы измерения тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы обычно используются, если изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. Собственно, параметрические методы и принято называть корреляционными. Непараметрические же методы не накладывают ограничений на закон распределения изучаемых величин. Они предполагают использование оценок-рангов. Их преимуществом является простота вычислений. В частности, к непараметрическим показателям связи относится коэффициент Фехнера. Поэтому в анализе социально-экономических явлений часто прибегают к условным оценкам с помощью рангов, а взаимосвязь между признаками измеряют с помощью непараметрических коэффициентов связи. Ранжирование – это упорядочение изучаемых объектов на основе предпочтения. Ранг – это порядковый номер индивидуальных значений признака, расположенных по возрастанию или убыванию. Оба признака необходимо ранжировать (нумеровать) в одном и том же порядке: от меньших значений к большим, и наоборот. Если несколько значений признака Вывод о наличии связи между изменениями значений признаков С помощью ранговых коэффициентов связи Спирмена Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле:
где Эта формула применяется в случае, если ранги не повторяются, т.е. ранги Коэффициент учитывает только разность рангов, а не самих значений, поэтому он менее точен по сравнению с линейным коэффициентом корреляции. Значимость коэффициента Спирмена проверяется на основе
Значение коэффициента корреляции считается статистически значимым (существенным), если Ранговый коэффициент корреляции Кендалла Расчет коэффициента ведется по формуле:
где Обычно коэффициент Кендалла меньше коэффициента Спирмена. Связь между признаками считается статистически значимой, если значения этих коэффициентов больше 0,5. При достаточно большом объеме совокупности между коэффициентами имеется следующая зависимость:
Расчет коэффициента Кендалла осуществляют по следующему алгоритму: 1. значения 2. значения 3. для каждого ранга 4. для каждого ранга 5. определяется сумма баллов S=P+Q по всем членам ряда. Таким образом, ранговые коэффициенты корреляции Спирмена и Кендалла имеют ряд преимуществ: § не требуется знать форму связи признаков; § простота расчетов; § возможность измерения связи не только между количественными, но и между ранжированными качественными (атрибутивными) признаками. Если число ранжируемых признаков (факторов) больше двух, то для измерения тесноты связи между ними используется коэффициент конкордации (множественный коэффициент ранговой корреляции)
где Эта формула применяется, если ранги по каждому признаку не повторяются (не связанные ранги). Значимость коэффициента конкордации проверяется на основе
Фактическое значение Значения коэффициента находятся в пределах от -1 до 1. Коэффициент конкордации позволяет: 1) определить степень согласованности мнений экспертов о важности того или иного оцениваемого показателя; 2) составить рейтинг отдельных единиц по какому-либо признаку. Поэтому наиболее часто он используется в экспертных оценках.
Контрольные вопросы 1. Какая связь называется функциональной? В каких случаях она применяется? 2. Какая связь называется стохастической? В каких случаях она применяется? 3. Что называется корреляцией? 4. Опишите основные виды корреляционных связей. 5. В чем состоят задачи изучения взаимосвязей между явлениями? 6. В чем состоит корреляционно-регресионный анализ связей? 7. Какие статистические методы используются для выявления корреляционных связей? 8. Что называется регрессией? 9. С какой целью применяется уравнение регрессии? 10. Как определяются параметры уравнения регрессии? 11. Что показывает коэффициент эластичности? 12. Что характеризует уравнение множественной регрессии? 13. Какие показатели применяются для оценки тесноты связи между количественными признаками? 14. Как оценивается существенность (значимость) линейного коэффициента корреляции. 15. Как определяется теснота и направление связи с помощью линейного коэффициента корреляции. 16. Как определяется теснота связи с помощью корреляционного отношения? 17. В каких случаях применятся множественный коэффициент корреляции? 18. Какие показатели применяются для оценки тесноты связи между качественными признаками? 19. Что представляют собой коэффициенты корреляции рангов Спирмена и Кендалла? 20. Что такое коэффициент конкордации? Как он рассчитывается? 21. Как определяется значимость коэффициента конкордации? Заключение Изучение статистики в сфере высшего профессионального образования направлено на формирование знаний и умений, необходимых специалисту туризма для выполнения своих должностных обязанностей. Эффективное развитие туризма и туристской индустрии зависит от наличия оперативной, достоверной и полной статистической информации. Она формируется в результате статистического наблюдения, которое является начальной стадией экономико-статистического исследования. Именно статистические данные позволяют определить объемы валового внутреннего продукта и национального дохода, выявить основные тенденции развития отраслей экономики, оценить уровень инфляции, проанализировать состояние финансовых и товарных рынков, исследовать уровень жизни населения и другие социально-экономические явления и процессы. Статистическое изучение процессов в индустрии туризма направлено на решение следующих задач: 1. получение объективной и достоверной информации о состоянии и развитии туристской отрасли; 2. оценка доли туризма в общей величине валового внутреннего продукта; 3. оценка туристских потоков и нагрузки на туристскую инфраструктуру; 4. оценка удовлетворения туристского спроса. Систематизированная статистическая информация является основой для построения модели развития туризма на региональном и национальном уровнях. Таким образом, предлагаемое учебное пособие должно помочь будущему работнику сферы туризма и гостеприимства применять основные приемы обработки статистических данных и методы вычисления статистических показателей.
Приложения Приложение 1 Значения функции
Примечание. Значения ординат увеличены в 10 000 раз Приложение 2 Значения интеграла вероятностей
Приложение 3 Таблица случайных чисел
Приложение 4
Распределение Стьюдента (
Приложение 5 Значения
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.37.200 (0.009 с.) |

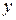

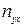



 преобразовывают следующим образом:
преобразовывают следующим образом: .
.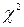 - критерия. Если ввести обозначение
- критерия. Если ввести обозначение  , то получим формулу:
, то получим формулу: =
=  ,
, - наиболее распространенный критерий согласия (применяется для проверки статистической гипотезы о виде распределения).
- наиболее распространенный критерий согласия (применяется для проверки статистической гипотезы о виде распределения). ,
, - число строк в таблице;
- число строк в таблице; 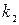 - число граф в таблице.
- число граф в таблице. ,
, и
и  - средние величины в группах;
- средние величины в группах;  - среднее квадратическое отклонение фактических значений признака от его среднего уровня;
- среднее квадратическое отклонение фактических значений признака от его среднего уровня; 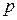 - доля первой группы;
- доля первой группы; 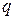 - доля второй группы;
- доля второй группы;  - табличные значения
- табличные значения  - распределения в зависимости от значений
- распределения в зависимости от значений  , Кендалла
, Кендалла  и конкордации (
и конкордации ( ) можно оценивать и измерять связь, как между количественными, так и между качественными признаками, которые поддаются ранжированию (рейтинги, квалификации и т.п.).
) можно оценивать и измерять связь, как между количественными, так и между качественными признаками, которые поддаются ранжированию (рейтинги, квалификации и т.п.). ,
,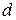 - разность рангов
- разность рангов 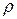 =0, то связь между признаками отсутствует. При
=0, то связь между признаками отсутствует. При  - критерия Стьюдента (Приложение 5). Фактическое (расчетное) значение критерия определяется по формуле:
- критерия Стьюдента (Приложение 5). Фактическое (расчетное) значение критерия определяется по формуле: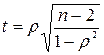 .
.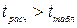 (
( ;
;  ).
). ,
, - сумма разностей между числом последовательностей и числом инверсий по второму признаку.
- сумма разностей между числом последовательностей и числом инверсий по второму признаку.
 (фиксируется со знаком «минус»);
(фиксируется со знаком «минус»); ,
, - число ранжируемых признаков (количество факторов);
- число ранжируемых признаков (количество факторов); 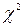 - критерия Пирсона:
- критерия Пирсона:
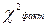 сравнивается с табличным
сравнивается с табличным  (Приложение 6) при уровне значимости
(Приложение 6) при уровне значимости 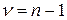 . Если
. Если