
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка тесноты линейной и нелинейной связиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таким образом, в аналитических группировках для характеристики тесноты связи между признаками сопоставляют межгрупповую дисперсию с общей дисперсией. Такое сопоставление называется корреляционным. Корреляционное отношение характеризует долю вариации результативного признака, вызванную действием факторного признака, положенного в основание группировки. Для измерения тесноты связи трех и более признаков одновременно, вычисляется множественный коэффициент корреляции. Он применяется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. Множественный коэффициент корреляции вычисляется по формуле:
где
Если необходимо оценить тесноту связи между результативным
где Множественный коэффициент корреляции положителен, изменяется в пределах от 0 до 1. Приближение значения Частные коэффициенты корреляции позволяют определить степень тесноты связи между результативным признаком Расчеты ведутся по формулам:
где При этом в первом случае исключено влияние факторного признака При небольшом количестве данных может применяться простейший показатель тесноты связи - коэффициент Фехнера
где Таким образом, коэффициент Фехнера предполагает подсчет совпадений и несовпадений знаков отклонений индивидуальных значений каждого признака
Если знаки всех отклонений по каждому признаку совпадут, то Коэффициент Фехнера показывает наличие и направление связи. Он может принимать значения от -1 до +1. Чем ближе значение коэффициента к единице, тем сильнее связь между признаками. Наличие корреляционной связи с помощью специальных коэффициентов можно определить и для качественных признаков. Показатели тесноты связи между качественными признаками
Важной задачей статистики является изучение социально-экономических явлений, не имеющих количественной оценки. Количественная оценка связей таких явлений осуществляется с помощью специальных показателей. Для оценки тесноты связи между качественными признаками используются следующие показатели: § коэффициенты ассоциации § коэффициенты взаимной сопряженности Пирсона § модификации коэффициентов Пирсона и Чупрова; § биссериальный коэффициент корреляции Эти коэффициенты применяются для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности. Коэффициенты ассоциации и контингенции применяются для определения тесноты связи двух качественных признаков, каждый из которых является альтернативным (состоит только из двух групп). Для их вычисления строится таблица «четырех полей», содержащая частоты Таблица 10.5 Таблица для вычисления коэффициентов ассоциации и контингенции
Расчеты ведутся по следующим формулам. Коэффициент ассоциации: Коэффициент контингенции: Значение коэффициента контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Если каждый из качественных признаков состоит более чем из двух групп, то теснота связи измеряется с помощью коэффициентов взаимной сопряженности Пирсона
где
Коэффициенты изменяются в пределах от 0 до 1, направления связи не показывают. Чем ближе значения Для расчета коэффициента взаимной сопряженности используется специальная вспомогательная таблица (табл. 10.6). Таблица 10.6 Вспомогательная таблица
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.209.24 (0.011 с.) |



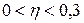
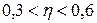

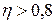

 ,
,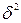 - дисперсия теоретических значений результативного признака, определенная по уравнению множественной регрессии;
- дисперсия теоретических значений результативного признака, определенная по уравнению множественной регрессии; - общая дисперсия результативного признака;
- общая дисперсия результативного признака; - остаточная дисперсия.
- остаточная дисперсия. и двумя факторными признаками
и двумя факторными признаками  , то применяется формула:
, то применяется формула: ,
, - парные коэффициенты корреляции между признаками.
- парные коэффициенты корреляции между признаками. к единице свидетельствует о сильной зависимости между признаками.
к единице свидетельствует о сильной зависимости между признаками.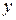 и каждым из факторных признаков при исключении влияния других факторных признаков.
и каждым из факторных признаков при исключении влияния других факторных признаков. ;
;  ,
, - парные коэффициенты корреляции между указанными в индексе переменными.
- парные коэффициенты корреляции между указанными в индексе переменными. , а во втором -
, а во втором - 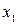 . Величина частных коэффициентов находится в пределах от 0 до 1.
. Величина частных коэффициентов находится в пределах от 0 до 1. (коэффициент корреляции знаков):
(коэффициент корреляции знаков): ,
, - соответственно количество совпадений и несовпадений отклонений величин факторного
- соответственно количество совпадений и несовпадений отклонений величин факторного  и результативного
и результативного  от своей средней величины, т.е.
от своей средней величины, т.е.  . Тогда получают отношение разности числа пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц.
. Тогда получают отношение разности числа пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц. . В этом случае
. В этом случае  . Тогда
. Тогда  , то
, то  и контингенции
и контингенции 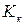 ;
; и Чупрова
и Чупрова 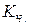 ;
;

 и
и 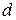 двух альтернативных признаков
двух альтернативных признаков 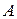 и
и  (табл. 10.5).
(табл. 10.5). (нет)
(нет)


 ( нет)
( нет)


 или
или 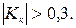
 ;
;  ,
,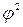 - показатель взаимной сопряженности;
- показатель взаимной сопряженности; - число значений (групп) первого признака;
- число значений (групп) первого признака;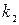 - число значений (групп) второго признака;
- число значений (групп) второго признака; - сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки за минусом единицы.
- сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки за минусом единицы.


