Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение теоретической формы связи в корреляционном анализе.Содержание книги
Поиск на нашем сайте
При исследовании корреляционных связей между качественными признаками, представленными в виде альтернативных показателей, используют коэффициент ассоциации Юла (Ка) и коэффициент контингенции Пирсона (Кк). Например: Коэффициент ассоциации:
Ка = (а·d – b·c) ÷ (а·d + b·c). В тех случаях, когда один из показателей отсутствует, величина коэффициента ассоциации будет равна 1, что дает неправильную оценку степени тесноты связи между признаками. В этом случае используют коэффициент контингенции:
Кк изменяется от –1 до +1, Кк < Ка всегда. Чем ближе коэффициент контингенции к единице, тем сильнее связь между факторным и результативным признаками. ДА НЕТ
ДА а в
НЕТ с d, Критерий адекватности математически функций в корреляци-м анализе. Критерий фишера. Для оценки значимости индекса корреляции применяется F-критерий Фишера.
Где m – число параметров корреляционного уравнения. Величина FR – сравнивается с критическим значением FK. Если FR> FK, то величина R признается существенной и синтезированная математическая модель может быть пригодной для практического использования. . в качестве критерия адекватности синтезируемых моделей использ-ся показатели минимальности сркдней ошибки аппроксимации.
Проверка типичности параметров уравнения регрессии и значимости коэфициента и индекса корреляции. Прежде чем использовать к-л модель в последующем анализе необходима проверка ее параметров на типичность T-критерий стьюдента
полученные значения ta0 ta1, сравниваются с tкритическим, кот получают по таблице, с учетом принятого уровня значимости альфа (5%ошибка) и числа степеней свободы к=n-m, n-число ед-ц совокупности, m-число параметров,критерий Стьюдента должен быть больше tкритического
ta0>tr<ta1, тогда параметры уравнения признаются типичными.
t-критерий Стьюдента для кэф-та корреляции
49.Множественная корреляция, Множ-ая кррел-я - при которой производится анализ влияния на результативный признак двух или более признаков факторов. Уравнение регрессии y=a0+a1x1+.....+anxm Введем матричные обозначения Х-матрица независ-х перемен-х(признак факора
Матрица параметров Уравнение регрессии в матричном виде
Непараметрические методы оценки корреляционной связи показателей. Для определения тесноты связи, как между количественными, так и между качественными признаками используется коэффициенты Фехнера и Спирмена. Коэффициент Фехнера вычисляется на основании определения знаков отклонения взаимосвязанных признаков x и y от их средних значений. Затем определяем число совпадений знаков отклонений для x и у, которое обозначается через а, а число несовпадений – через b, тогда коэффициент будет равен:
i = (Σa – Σb) ÷ (Σa + Σb), чем ближе i к 1, тем связь теснее, чем i ближе к 0 - тем слабее. Если значение признаков упорядочены (проранжированный) по степени убывания или возрастания признака, можно использовать для определения тесноты связи коэффициент рангов Спирмена:
р = 1 – (6 · Σdi²) ÷ (N · (N в квадрате – 1)), где N – число наблюдений (число пар рангов)., di в квад-те—квадрат разости рангов связанных величинами х и у Для определения d величины x и y сначала располагают в порядке увеличения, а затем производят ранжирование. Далее ранги записываются в соответствии с первоначальным расположением величин x и y и сравниваются между собой. Получают разность рангов величин x и y, равную d. Секторно-отраслевая классиф-я.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.232.87 (0.008 с.) |

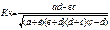
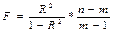
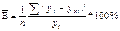 , где уi-yxi линейное отклонение абсолютных велечин эмпирических и выравненых точек регрессии. Для прямой 21,6%, для полулогарифмической 25,2%
, где уi-yxi линейное отклонение абсолютных велечин эмпирических и выравненых точек регрессии. Для прямой 21,6%, для полулогарифмической 25,2%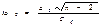
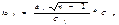
 -среднеквадратическое отклонение результативного признака от выравненного значения
-среднеквадратическое отклонение результативного признака от выравненного значения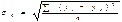
 -среднеквадратическое отклонение признака фактора от его сред-го знач-я
-среднеквадратическое отклонение признака фактора от его сред-го знач-я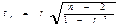
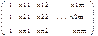
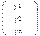 =у
=у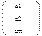 =а
=а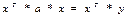
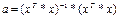
 транспонированная матрица. Транспон-е-операция переноса строк исходной матрицы в положение столбцов
транспонированная матрица. Транспон-е-операция переноса строк исходной матрицы в положение столбцов