
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние величины их сущность значение. Основные правила применения в ста-ке. Правило мажорности средних.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средние величины – это обобщающие показатели, в которых находят выражение действия общих условий, закономерность изучаемого явления. Признак по кот нах-ся средняя наз осредняемым и обознач Средняя арифметическая: Средняя квадратическая: Средняя гармоническая: Средняя геометрическая: где
Выше были приведены простые средние. Их используют только тогда, когда у каждой варианты частота равна единице или частоты всех вариант равны. Когда в ряду распределения одно и то же значение признака встречается несколько раз, рассчитывают средние взвешенные:
- средняя арифметическая, где f – частота (весы), повторяемость индивидуальных значений признака. Взвешивание – это умножение каждой варианты на соответствующую частоту. Средняя арифметическая используется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.
Средняя арифметическая (простая и взвешенная) Ее св-ва Средние величины – это обобщающие показатели, в которых находят выражение действия общих условий, закономерность изучаемого явления. Признак по кот нах-ся средняя наз осредняемым и обознач Средняя арифметическая: Среднеарифм примен-ся когда объем варьирующего признака опр-ся как сумма отдельных вариантов. Ср.арифм простая опр-ся когда у каждой варианты частота = 1 или частоты всех вариант =.В том случае когда у вариант разные вычисл-ся сред арифм взвешенную на основе вариационного ряда. Умножение каждой варианты на соответ-ю частоту наз взвешиванием Св-ва 1.увелич-е или уменьш-е частоты каждого значения признака в n раз не влияет на величину сред.арифм. 2. если каждое знач признака ум-ть или разделить на кокое-либо чило А то велич-а сред уменьш или увел в А раз
3. 4.если варианта явл неизменной, то среднее этих величин будет тоже постоянная величина
5.сумма отношений вар-т от их сред значения =0 ВЗВЕШЕННЫЕ СРЕДНИЕ Когда в ряду распределения одно и то же значение признака встречается несколько раз, рассчитывают средние взвешенные. Взвешивание – это умножение каждой варианты на соответствующую частоту. Число единиц имеющих одинаковое значение признаков наз весами или частотами с ко варианта входит в среднее. При вычислении из всех вриантов одной какой-либо варианты, мы мысленно приравниваем эту варианту к 0. Это и есть условное начало нового ряда. Ср ар этих новых вариант наз моментом первого порядка. Средняя гармоническая используется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.
где 19.СТРУКТ ср (медиана,мода..) Показатели, характеризующие структуру совокупности, называются структурными средними. Это мода и медиана.Мода (Мо) – чаще всего встречающийся вариант признака. В дискретном вариационном ряду – это варианта с наибольшей частотой – 37 размер. В интервальном вариационном ряду мода – это центральный вариант модального интервала (f=max). В пределах интервала находится мода.
где X mo – нижняя граница модального интервала; i mo – величина модального интервала; f mo – частота, соответствующая модальному интервалу; f mo -1 – частота, предшествующая модальному интервалу; f mo +1 – частота интервала следующего за модальным. Медиана (Ме) – величина, кот. делит численность вариационного ряда на две равные части.
В интервальном вариационном ряду (медианный интервал будет там, где накопленная частота составляет половину или больше половины численности совокупности) медиана определяется по формуле: где Xme – нижняя граница медианного интервала; ime - величина медианного интервала;
Дополнительно к ме для хар-ки стр исчисляют квартили, ко делят ряд по сумме частот на 4 равных частных, и децили ко делят вар ряд на 10 равных частей
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.70.169 (0.008 с.) |

 и величина осредненного признака у каждой ед-цы сов-ти наз индивидуализ-ым ее значением или вариантой Повторяемость вариант наз частота.
и величина осредненного признака у каждой ед-цы сов-ти наз индивидуализ-ым ее значением или вариантой Повторяемость вариант наз частота. ; (простая)
; (простая) ;
; ;
; ,
, - осредняемый признак,
- осредняемый признак,  - варианта, n – число вариант, П – знак перемножения.
- варианта, n – число вариант, П – знак перемножения. - правило мажорности средних.
- правило мажорности средних. - средняя гармоническая, где
- средняя гармоническая, где 
 ; (простая)
; (простая)






 - средняя арифметическая взвешенная где f – частота (весы), повторяемость индивидуальных значений признака.
- средняя арифметическая взвешенная где f – частота (весы), повторяемость индивидуальных значений признака.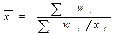 - средняя гармоническая,
- средняя гармоническая,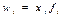
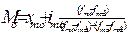 ,
,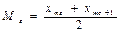
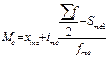 ,
, - полусумма частот ряда; Sme-1 – сумма накопленных частот, предшествующих медианному интервалу; fme – частота медианного интервала.
- полусумма частот ряда; Sme-1 – сумма накопленных частот, предшествующих медианному интервалу; fme – частота медианного интервала.


