
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 9. Статистическое изучение взаимосвязи социально-экономических явленийСодержание книги
Поиск на нашем сайте
Основные понятия Все социально-экономические явления взаимосвязаны. Связь между ними носит причинно-следственный характер. Признаки, характеризующие причины и условия связи, называются факторными (х), а те, которые характеризуют последствия связи, - результативными (у). Между признаками х и у возникают разные по природе и характеру связи, в частности функциональные и стохастические. При функциональной связи каждому значению признака х отвечает одно четко определенное значение у. Эта связь проявляется однозначно в каждом конкретном случае. При стохастической связи каждому значению признака х отвечает определенное множество значений у, которые образовывают так называемое условное распределение. Как закон эта связь проявляется только в массе случаев и характеризуется изменением условных распределений у. Если заменить условные распределения средней величиной у, то образуется разновидность стохастической связи – корреляционная. В случае корреляционной связи каждому значению признака х отвечает среднее значение результативного признака у. Примером стохастической и, в частности, корреляционной связи является распределение проданных на бирже недвижимости однокомнатных квартир по их стоимости у и размеру общей площади х (табл. 9.1).
Таблица 9.1 – Распределение проданных на бирже недвижимости однокомнатных квартир по их стоимости и размеру на 1.01.2010 г.
Каждой группе по факторному признаку отвечает свое распределение у, которое отличается от других групп и от безусловного итогового распределения. Следовательно, наблюдается стохастическая связь между признаками. Условные распределения можно заменить средними значениями результативного признака, которые вычисляют как среднюю арифметическую взвешенную. Постепенное изменение средних Характеристикой корреляционной связи является линия регрессии, которую рассматривают в двух моделях - аналитической группировки и регрессионного анализа. В модели аналитической группировки это эмпирическая линия регрессии, которая образовывается из групповых средних значений результативного признака Эффекты воздействия х на у определяют как отношение приростов средних групповых значений:
По данным таблицы 9.1 приросты
Следовательно, с увеличением размера общей площади квартир на 1 м² их стоимость в среднем растет соответственно на:
Оценка плотности связи основывается на правиле сложения дисперсий. В модели аналитической группировки мерой плотности связи выступает отношение межгрупповой дисперсии к общей, которое называется корреляционным отношением:
где
Корреляционное отношение колеблется от нуля до единицы, а если выразить в процентах, то от 0 до 100 %. При отсутствии связи По данным таблицы 9.1 общая дисперсия стоимости проданных квартир будет равна:
В таблице 9.2 приведена аналитическая группировка проданных квартир, которая описывает зависимость их стоимости от общей площади. Там же дан расчет межгрупповой дисперсии.
Таблица 9.2 – Аналитическая группировка проданных на бирже квартир
Корреляционное отношение
следовательно, вариация стоимости проданных квартир на 66 % объясняется вариацией их общей площади и на 34 % - вариацией других факторов, т.е. связь между признаками достаточно плотная. Однако плотная связь может возникнуть случайно, поэтому необходимо проверить ее тесноту, т.е. доказать неслучайность связи. Проверка тесноты связи – это сравнение фактического значения В нашем примере Поскольку В модели регрессивного анализа характеристикой корреляционной связи является теоретическая линия регрессии, описываемая функцией - линейные уравнения - нелинейные уравнения, когда изменение взаимосвязанных признаков происходит неравномерно (с ускорением, замедлением или с переменным направлением связи), в частности: степенное Чаще применяют линейные уравнения или приведенные к линейному виду. В линейном уравнении параметр b - коэффициент регрессии указывает, на сколько единиц в среднем изменится у с изменением х на единицу. Он имеет единицу измерения результативного признака. В случае прямой связи b – величина положительная, а при обратной - отрицательная. Параметр a – свободный член уравнения регрессии, т.е. это значение Y при х = 0. Если х не приобретает нулевые значения, то данный параметр имеет только расчетное значение. Параметры определяются методомнаименьших квадратов, согласно которому сумма квадратов отклонений эмпирических значений у от Y минимальна:
Отсюда
Для расчета параметров уравнения параболы второго порядка методом наименьших квадратов система нормальных уравнений имеет следующий вид:
Коэффициент регрессии в небольших по объему совокупностях подвержен случайным колебаниям. Поэтому проверяют его существенность с помощью t критерия (Стьюдента):
где b – коэффициент регрессии;
где n – объем совокупности. Характеристикой относительного изменения у вследствие изменения х есть коэффициент эластичности:
который показывает, на сколько процентов в среднем меняется результативный признак с изменением факторного на 1 %. На основании уравнения регрессии определяют теоретические значения Y, т.е. значение результативного признака при условии воздействия только фактора х при неизменном уровне других факторов. Отклонения эмпирических значений у от теоретических Y называют остаточными. Они характеризуют воздействие на результативный признак всех других факторов, кроме х. Средний размер этих отклонений определяет остаточная дисперсия
Вариацию у, обусловленную воздействием только фактора х, называют факторной дисперсией:
Доля факторной дисперсии в общей характеризует плотность связи и называется коэффициентом детерминации:
Он имеет такой же смысл, интерпретацию и цифровые границы, что и Плотность связи оценивается также индексом корреляции
который принимает значения в границах Абсолютное значение r равно индексу корреляции:
Однако для интерпретации r необходимо перейти к уравнению Проверка существенности связи в обеих моделях может определяться также по критерию Фишера, который функционально связан с
или
поэтому процедура проверки и выводы идентичны.
Тест Выберите правильный ответ: 1. По направлению связи бывают: а) умеренные; б) прямые; в) прямолинейные. 2. Функциональной является связь: а) между двумя признаками; б) при которой определенному значению факторного признака соответствует несколько значений результативного признака; в) при которой определенному значению факторного признака соответствует одно значение результативного признака. 3. Математическое выражение коэффициента линейной корреляции имеет следующий вид:
4. С помощью корреляционно-регрессионного анализа изучают следующие типы взаимосвязей между явлениями: а) компонентные; б) факторные; в) балансовые. 5. Факторный признак – это: а) признак, обуславливающий изменение другого, связанного с ним; б) признак, изменяющийся под воздействием другого. 6. Зависимость между результативным и одним факторным признаком при фиксированном значении других признаков – это: а) множественная корреляция; б) частная корреляция; в) парная корреляция. 7. Изменение тесноты, направления связи и установление аналитического выражения связи носит название: а) корреляционного анализа; б) корреляционно-регрессионного анализа; в) регрессионного анализа. 8. Коэффициент детерминации (d) выражается следующим образом:
9. Косвенные связи имеют место в случае: а) когда факторы взаимодействуют между собой непосредственно; б) когда связь устанавливается формально, подтверждаясь только количественными оценками; в) когда связь характеризуется участием какой-либо переменной, опосредующей связь между изучаемыми признаками. 10. Установление формы зависимости, определение функции регрессии, использование уравнения для оценки значений зависимой переменной – это задачи: а) регрессионного анализа; б) корреляционного анализа; в) корреляционно-регрессионного анализа. 11. Анализ тесноты и направления связей двух признаков осуществляется на основе: а) парного коэффициента корреляции; б) частного коэффициента корреляции; в) множественного коэффициента детерминации. 12. Для проверки типичности параметров уравнения регрессии используется: а) критерий Фишера; б) среднее квадратическое отклонение; в) критерий Стьюдента. 13. Аналитическое выражение связи определяется с помощью методов анализа: а) корреляционного; б) регрессионного; в) группировок. 14. Показателем, показывающим, какая часть общей вариации результативного признака объясняется изучаемым признаком - фактором, является: а) коэффициент детерминации; б) индекс корреляции; в) индекс регрессии. 15. Коэффициент эластичности
16. Для расчета коэффициента множественной корреляции применяется формула: а) б) в) Задачи Примеры решения задач Пример 1. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделий в генеральной совокупности. Решение: Сначала рассчитаем предельную ошибку выборки. Так, при р = 0,997, t = 3. При случайном повторном отборе предельная ошибка выборки определяется по формуле:
Определим пределы генеральной средней:
30 – 0,84 Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 до 30,84 г. Пример 2. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2 %-я случайная бесповторная выборка семей. По её результатам было получено следующее распределение семей по числу детей (табл. 9.1). Таблица 9.1 – Распределение семей по числу детей в городе в 2010 г.
С вероятностью 0,954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности. Решение: вначале на основе имеющегося распределения семей определим выборочную среднюю и дисперсию. Для удобства расчет оформим в виде таблицы 9.2.
Таблица 9.2 – Вспомогательные расчеты для определения дисперсии и выборочной средней
Вычислим теперь предельную ошибку выборки (с учетом того, что p = 0,954 и t = 2). Для случайной бесповторной выборки предельная ошибка вычисляется по формуле:
Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0,954 можно утверждать, что в среднем на каждые две семьи приходятся три ребенка. Пример 3. С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин. На основании предыдущих обследований было известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 (t = 3) и ошибке 5 %. Решение: рассчитаем общую численность типической бесповторной выборки:
Вычислим объем отдельных типических групп:
Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 550 человек, в том числе 321 мужчина и 231 женщина.
Задачи 1. В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 (t = 2) рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5 %.
2. Каким должен быть объём случайной бесповторной выборки из генеральной совокупности численностью 10000 единиц при среднем квадратическом отклонении не более 20, предельной ошибке, не превышающей 5 %, и вероятности 0,997 (t = 3).
3. Из партии импортируемой продукции на посту таможни было взято в порядке случайной бесповторной выборки 20 проб продукта А. В результате проверки установлена средняя влажность продукта А в выборке, которая оказалась равной 6 % при среднем квадратическом отклонении 1 %. С вероятностью 0,683 (t = 1) определите пределы средней влажности продукта во всей партии импортируемой продукции.
4. С целью определения средних затрат времени при поездках на работу населением города планируется выборочное обследование на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 (t = 2) ошибка выборочной средней не превышала 1 мин. при среднем квадратическом отклонении 15 мин.
5. В одном из лесничеств области методом случайной выборки обследовано 1000 деревьев с целью установления их среднего диаметра, который оказался равным 210 мм при
6. Из партии в 1 млн шт. мелкокалиберных патронов путем случайного отбора взято для определения дальности боя 1000 шт. Результаты испытаний представлены в таблице 9.3.
Таблица 9.3 – Распределение мелкокалиберных патронов по дальности боя
С вероятностью 0,954 (t = 2) определите среднюю дальность боя по выборке, ошибку выборки и возможные пределы средней дальности боя всей партии патронов.
7. В порядке механической выборки обследован возраст 100 студентов вуза из общего числа 2000 человек. Результаты обработки материалов наблюдения приведены в таблице 9.4. Таблица 9.4 – Распределение студентов вуза по возрасту на 15.09.10 г.
Установите: а) средний возраст студентов вуза по выборке; б) величину ошибки при определении возраста студентов на основании выборки; в) вероятные пределы колебания возраста для всех студентов при вероятности 0,997 (t = 3).
8. С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек в июне 2010 г. была проведена 25 %-я механическая выборка. По результатам наблюдения оказалось, что у 10 % обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 (t = 1) установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
9. В области, состоящей их 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5; 16; 15,5 и 14 ц/га. С вероятностью 0,954 (t = 2) найдите пределы урожайности во всей области.
10. В 100 туристических агентствах города предполагалось провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала три путевки, если по данным пробного обследования дисперсия составляет 225? РАЗДЕЛ 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.013 с.) |



 для каждого значения (интервала)
для каждого значения (интервала)  .
.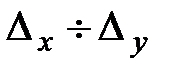 , где
, где 
 .
. во всех группах одинаковы – 5 м², а средняя стоимость проданных квартир увеличивается по группам следующим образом:
во всех группах одинаковы – 5 м², а средняя стоимость проданных квартир увеличивается по группам следующим образом: тыс. усл. ед.;
тыс. усл. ед.; 

 тыс. усл. ед. и на 0,4 и 0,56.
тыс. усл. ед. и на 0,4 и 0,56. ,
,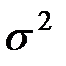 – общая дисперсия, которая измеряет вариацию результативного признака у, обусловленную воздействием всех возможных факторов;
– общая дисперсия, которая измеряет вариацию результативного признака у, обусловленную воздействием всех возможных факторов;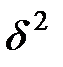 – межгрупповая дисперсия, которая измеряет вариацию результативного признака у под воздействием только группировочного признака х.
– межгрупповая дисперсия, которая измеряет вариацию результативного признака у под воздействием только группировочного признака х.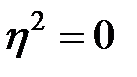 , а при условии функциональной связи
, а при условии функциональной связи  Чем больше
Чем больше 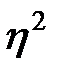 приближается к единице, тем более плотная связь.
приближается к единице, тем более плотная связь.
 , м²
, м²



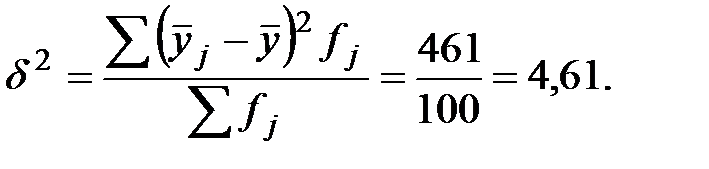

 с его критическим значением
с его критическим значением  для определенного уровня тесноты α и числа степеней свободы
для определенного уровня тесноты α и числа степеней свободы  и
и  , где
, где  - число групп,
- число групп,  - объем совокупности. Если
- объем совокупности. Если  >
>  , то связь признается существенной. Критические значения корреляционного отношения для
, то связь признается существенной. Критические значения корреляционного отношения для  приведены в специальных таблицах.
приведены в специальных таблицах.
 Из-за отсутствия в таблице критических значений
Из-за отсутствия в таблице критических значений  используем ближайшее (
используем ближайшее ( ), тогда
), тогда  .
. то связь признается существенной с вероятностью 0,95.
то связь признается существенной с вероятностью 0,95.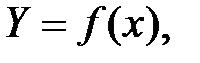 которая называется уравнением регрессии. В зависимости от характера связи используют:
которая называется уравнением регрессии. В зависимости от характера связи используют: когда с изменением х признак у изменяется более или менее равномерно;
когда с изменением х признак у изменяется более или менее равномерно; гиперболическое
гиперболическое  параболическое
параболическое  и т.п.
и т.п. В соответствии с условием минимизации параметры линейного уравнения регрессии вычисляют на основании системы нормальных уравнений:
В соответствии с условием минимизации параметры линейного уравнения регрессии вычисляют на основании системы нормальных уравнений:


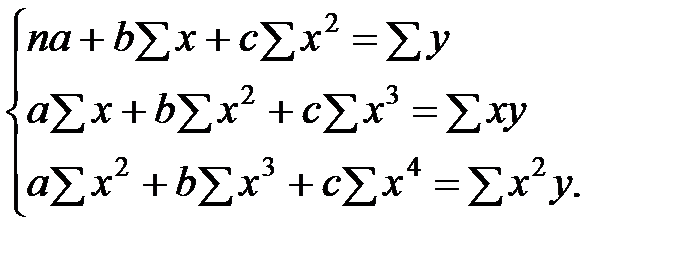
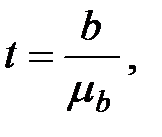
 - стандартная погрешность, которую рассчитывают по формуле:
- стандартная погрешность, которую рассчитывают по формуле:

 – соответственно остаточная и факторная дисперсии;
– соответственно остаточная и факторная дисперсии;
 .
.


 , однако интерпретируется только
, однако интерпретируется только 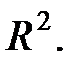 Для линейной связи используют линейный коэффициент корреляции (Пирсона) r:
Для линейной связи используют линейный коэффициент корреляции (Пирсона) r:
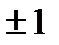 , поэтому характеризует не только плотность, но и направление связи. Положительное значение свидетельствует о прямой связи, а отрицательное – об обратной.
, поэтому характеризует не только плотность, но и направление связи. Положительное значение свидетельствует о прямой связи, а отрицательное – об обратной.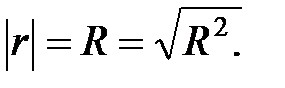
 Проверка существенности связи выполняется таким же образом, как и в модели аналитической группировки, путем сравнения
Проверка существенности связи выполняется таким же образом, как и в модели аналитической группировки, путем сравнения  и
и  Отличия касаются только определения
Отличия касаются только определения 
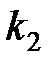 , в которых m – число параметров уравнения регрессии.
, в которых m – число параметров уравнения регрессии. и
и  :
:
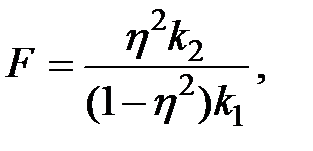
 ;
;
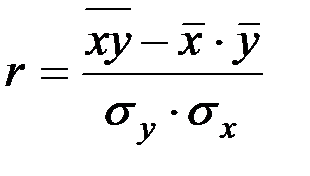 ;
;

 ;
;
 ;
;
 .
.
 определяется следующим образом:
определяется следующим образом: ;
;
 ;
;
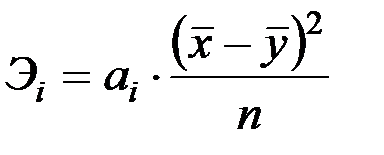 .
.
 ;
;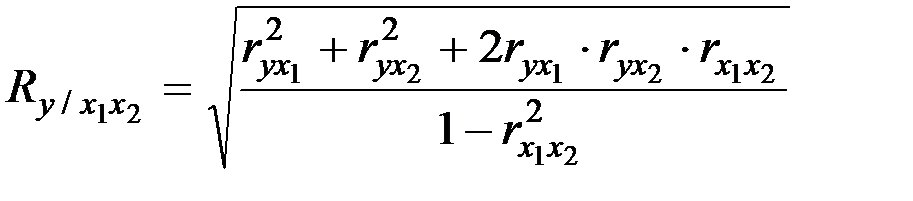 ;
; .
.
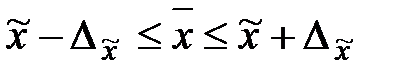 .
. 30 +0,84, или 29,16
30 +0,84, или 29,16  30,84.
30,84.

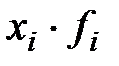


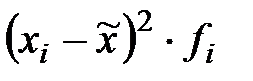
 чел.;
чел.;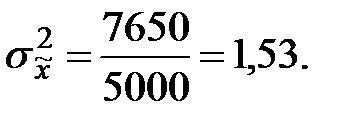
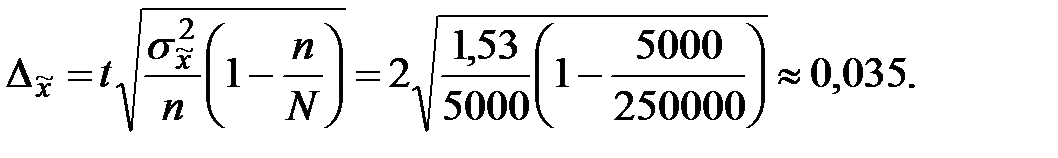

 человек.
человек. человек;
человек; человек.
человек. мм. С вероятностью 0,683 (t = 1) определите пределы среднего диаметра деревьев в генеральной совокупности.
мм. С вероятностью 0,683 (t = 1) определите пределы среднего диаметра деревьев в генеральной совокупности.


