
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мода – значение признака, наиболее часто встречающее в исследуемой совокупности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Для интервальных вариационных рядов мода определяется по формуле:
где
Медиана интервального ряда распределения определяется по формуле:
где
Тест Выберите правильный ответ. 1. Средняя величина – это: а) значение признака, находящееся в середине ряда распределения; б) обобщенная типическая характеристика признака в данной совокупности; в) значение признака, встречающееся чаще других. 2. Для расчета средней величины по несгруппированным данным в случае возможности их прямого суммирования следует применять формулу: а) арифметической простой; б) арифметической взвешенной; в) гармонической простой; г) гармонической взвешенной. 3. Для расчета общей средней по сгруппированным данным следует применить формулу средней: а) арифметической простой; б) арифметической взвешенной; в) гармонической простой; г) гармонической взвешенной. 4. Для определения общей средней из коэффициентов выполнения плана по показателю по нескольким предприятиям следует применить формулу средней: а) арифметической простой; б) арифметической взвешенной; в) гармонической простой; г) гармонической взвешенной. 5. Возможна ли многовариантность значений среднего показателя, рассчитанного по одним и тем же данным?
8. Для измерения вариации значения признака применяются следующие статистические показатели: а) средние величины; б) мода и медиана; в) размах вариации, среднее линейное отклонение, дисперсия, г) среднеквадратическое отклонение, коэффициент вариации. 9. Если все значения признака увеличить (уменьшить) на некоторую постоянную величину, то средняя арифметическая: а) не изменится; б) увеличится (уменьшится) на эту величину; в) уменьшится (увеличится на эту величину. 10. Если все значения признака умножить (разделить) на некоторую постоянную величину, то средняя арифметическая: а) не изменится; б) увеличится (уменьшится) во столько раз; в) уменьшится (увеличится) во столько раз. Задачи Примеры решения задач Пример 1. По данным таблицы 4.1 рассчитаем среднюю заработную плату в целом по трем предприятиям.
Таблица 4.1 – Заработная плата на предприятиях АО в 2011 г.
Определим исходное соотношение средней для показателя «Средняя заработная плата»:
Нам известен знаменатель исходного соотношения, но не известен числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность ППП. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
Допустим, что нам известны только данные о фонде заработной платы и средней заработной плате персонала (табл. 4.2), т.е. известен числитель исходного соотношения, но не известен его знаменатель.
Таблица 4.2 – Месячный фонд заработной платы и средняя заработная плата на предприятиях АО в 2011 г.
Численность работников по каждому предприятию можно получить делением фонда заработной платы на среднюю заработную плату. Тогда для расчета средней заработной платы мы будем использовать формулу средней гармонической взвешенной:
Пример 2. По данным таблицы 4.3 определим величину среднедушевого дохода по городу.
Таблица 4.3 – Распределение населения города в 1-м квартале 2009 г. по уровню среднедушевых денежных доходов
Так как мы имеем интервальный ряд, то определяем середины интервалов. При этом величину первого интервала условно приравниваем к величине второго, а величину последнего интервала приравниваем к величине предпоследнего. В результате получаем следующие середины интервалов:
Роль численности населения выполняет его доля в общем итоге, выраженная в процентах. Для расчета воспользуемся формулой средней арифметической взвешенной:
Пример 3. Рассчитаем моду и медиану по данным таблицы 4.4.
Таблица 4.4 – Распределение семей города по размеру среднедушевого дохода в январе 2011 г.
Следовательно, наибольшее число семей в январе 2011 г. имели среднедушевой доход 13,6 тыс. рублей.
Таким образом, половина семей города имели в январе 2011 г. среднедушевой доход менее 14 тыс. руб., остальные семьи – более 14 тыс. руб. Задачи 1. Рабочие бригады имеют следующий стаж работы на данном предприятии (табл. 4.5). Таблица 4.5 – Стаж рабочих бригады ЗАО «Промметалл»
Определите средний стаж работы.
2. Распределение рабочих предприятия по тарифному разряду имеет следующий вид (табл. 4.6). Таблица 4.6 – Распределение рабочих предприятия по тарифному разряду
Определите средний уровень квалификации рабочих предприятия.
3. Результаты торгов на российских биржах 1 июля 2010 г. характеризуются следующими данными (табл. 4.7).
Таблица 4.7 – Результаты торгов на российских биржах за 1.07.10 г.
Рассчитайте средний курс доллара.
4. По данным микропереписи 2011 г. получено следующее распределение населения, проживающего в месте постоянного жительства не с рождения (табл. 4.8).
Таблица 4.8 – Распределение населения, проживающего в месте постоянного жительства, на 1.01.11 г.
Определите среднюю продолжительность проживания в месте постоянного жительства для данной категории населения.
5. Имеются следующие данные по промышленным предприятиям области (табл. 4.9).
Таблица 4.9 – Распределение промышленных предприятий области по себестоимости 1 кг гвоздей на 1.06.09 г.
Определите среднюю себестоимость 1 кг гвоздей по предприятиям области.
6. Производственная деятельность одного из отделений корпорации за месяц характеризуется следующими данными (табл 4.10).
Таблица 4.10 – Производственная деятельность промышленного отделения корпорации за январь 2008 г.
Определите средние затраты на 1 руб. произведенной продукции в целом по отделению.
7. По трем районам города имеются следующие данные (на конец года) (табл. 4.11).
Таблица 4.11 – Характеристика районов города по вкладам в отделения Сбербанка на 1.01.10 г.
Определите средний размер вклада в Сбербанке в целом по городу.
8. Качество продукции предприятия характеризуется следующими данными (за месяц) (табл. 4.12).
Таблица 4.12 – Характеристика качества продукции предприятия за сентябрь 2010 г.
Определите средний процент брака в целом по предприятию.
9. В отделе заказов торговой фирмы занято трое работников, имеющих 8-часовой рабочий день. Первый работник на оформление одного заказа в среднем затрачивает 14 мин., второй – 15, третий – 19 мин. Определите средние затраты времени на один заказ в целом по отделу.
10. Использование складских помещений города характеризуется следующими данными (табл. 4.13).
Таблица 4.13 – Распределение складских помещений города по площади
Вычислите средний процент загрузки.
11. По данным таблицы 4.14 определите средний процент содержания никеля, модальный и медианный интервалы.
Таблица 4.14 – Содержание никеля по результатам анализа плавки легированной стали
12. При изучении качества семян пшеницы было получено следующее распределение семян по проценту всхожести (табл. 4.15).
Таблица 4.15 – Распределение семян по проценту всхожести в 2010 г.
Рассчитайте моду и медиану.
13. Вычислите моду и медиану количественного состава семей города на основании следующего их распределения по числу совместно проживающих членов семей (табл. 4.16).
Таблица 4.16 – Распределение семей города по числу совместно проживающих членов семьи на 1.12.12 г.
14. С целью исследования качества деталей на предприятии проверена партия из 100 деталей. Результаты представлены в таблице 4.17.
Таблица 4.17 – Распределений деталей на предприятии по весу на 1.07.10 г.
Вычислите моду и медиану значения веса деталей.
РАЗДЕЛ 2 АНАЛИТИЧЕСКАЯ СТАТИСТИКА
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1901; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.011 с.) |


 – нижняя граница значения интервала, содержащего моду;
– нижняя граница значения интервала, содержащего моду;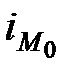 – величина модального интервала;
– величина модального интервала; – частота модального интервала;
– частота модального интервала; – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
 – нижняя граница значения интервала, содержащего медиану;
– нижняя граница значения интервала, содержащего медиану; – величина медианного интервала;
– величина медианного интервала; – сумма частот;
– сумма частот; – сумма накопленных частот, предшествующих медианному интервалу;
– сумма накопленных частот, предшествующих медианному интервалу; – частота медианного интервала.
– частота медианного интервала.
 тыс. руб.
тыс. руб.
 руб.
руб. .
. руб.
руб. тыс. руб.
тыс. руб.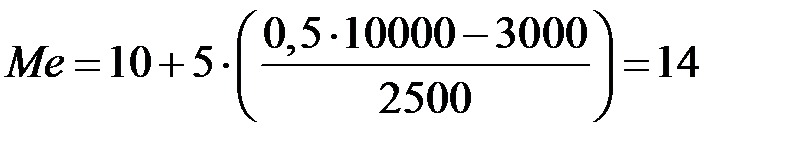 тыс. руб.
тыс. руб.


