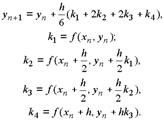Численное Интегрирование и дифференцирование

Интегрирование и дифференцирование — самые простые, с вычислительной точки зрения, операции, реализованные в Mathcad в виде операторов. Тем не менее, если расчеты выполняются с помощью вычислительного процессора, необходимо хорошо представлять себе особенности численных алгоритмов, действие которых остается для пользователя "за кадром" В тех же разделах упоминается и об особенностях символьных операций интегрирования и дифференцирования.

Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярами. Несмотря на то что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным. Если пределы интегрирования имеют размерность (, то она должна быть одной и той же для обоих пределов.

Интегрирование, дифференцирование, как и множество других математических действий, устроено в Mathcad по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа "&"). Появится символ интеграла с несколькими местозаполнителями (рис. 7.1), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.

Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести -> (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.

Дифференцирование.С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, от о-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными. Невозможно дифференцирование функций только вблизи точек их сингулярности. Вычислительный процессор Mathcad обеспечивает превосходную точность численного дифференцирования. Но больше всего пользователь оценит возможности символьного процессора, который позволяет с легкостью осуществить рутинную работу вычисления производных громоздких функций, поскольку, в отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций. В Mathcad 11 для ускорения и повышения точности численного дифференцирования функций, заданных аналитически, автоматически задействуется символьный процессор

 

Метод Рунге-Кутта

 

Ме́тоды Ру́нге-Ку́тты – важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями. Методы седьмого порядка должны иметь по меньшей мере девять стадий, в схему восьмого порядка входит 11 стадий. Хотя схемы девятого порядка не имеют большой практической значимости, неизвестно, сколько стадий необходимо для достижения этого порядка точности. Аналогичная задача существует для схем десятого и более высоких порядков

Программа работает на языке Turbo Pascal 7.0, по методу Рунге-Кутта.Решение систем дифференциальных уравнений методом Рунге-Кутты является одним из самых распространённых численных методов решений в технике. В среде MATLAB (довольно распространённый и удобный язык для технических вычислений) реализована его одна из разовидностей — метод Дорманда-Принса. Для решения системы уравнений необходимо сначала записать функцию, вычисляющую производные, т.е. функции y = g(x,y,z) и z = cos(3x) - 4y = f(x,y,z), о чём сказано выше. В одной из папок, к которой имеется доступ из системы MATLAB нужно создать текстовый файл с именем (например) runge.m со следующим содержимым (для MATLAB версии 5.3)

Метод Рунге–Кутта часто применяется для решения дифференциальных уравнений и систем уравнений из-за его высокой точности. Отличительная особенность метода – уточнение наклона интегральной кривой за счет вычисления производной не только в начале текущего отрезка интегрирования, но и, например, в середине отрезка (для двучленных схем Рунге–Кутта) или четырехкратное вычисление производных в методе четвертого порядка.

Для случая одного уравнения двучленная итерационная формула может иметь вид

y_n+1=y_n+h f(x_n+0,5h,y_n+0,5hf_n)

Последовательность вычислений: сначала делают половинный шаг по схеме ломаных (по формуле Эйлера), находя y_n+0,5=y_n+hy^’_n+0,5, затем в найденной точке определяют наклон кривой y^’_n+0,5=f(x_n+0,5, y_n+0,5) и по этому наклону определяют приращение на целом шаге y_n+1=y_n+ hy^’_n+0,5.

Четырехчленная схема Рунге–Кутта наиболее часто употребляется в машинных расчетах и имеет четвертый порядок точности:

Метод Рунге-Кутта легко переносится и на случай системы дифференциальных уравнений.

В библиотеку Mathlib включена процедура RKGS, реализующая метод Рунге-Кутта четвертого порядка с автоматическим выбором шага интегрирования

Замечание. Так как в процедуре шаг выбирается автоматически в зависимости от скорости изменения функций, обычно применяют следующий алгоритм: задаются требуемым шагом вывода результатов (в программе переменная sprint), определяют число шагов n, а затем процедуру RKGS вызывают n раз для последовательного интегрирования уравнений на этих участках, организуя вывод результатов после завершения процедуры.