
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая обработка статистических результатов исследования точности технологических процессовСодержание книги
Поиск на нашем сайте
Погрешности обработки деталей, вызываемые различными производственно-технологическими факторами, являются величинами случайными, что обуславливает необходимость применения в анализе точности методов теории вероятностей и математической статистики. Случайной величиной называется величина, которая в результате опыта может принять тo или иное значение [1]. Например, признак качества Х для партии деталей объемом n, изготовленной в одной технологической операции, есть величина случайная, так как каждая деталь будет характеризоваться своим значением признака качества Основной теоретической числовой характеристикой случайной величины является вероятность ее появления P, которая позволяет принимать любое значение от 0 до 1 включительно
Сумма вероятностей всех возможных значений случайной величины
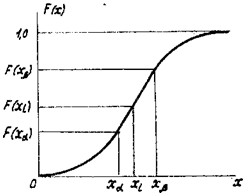
Эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины. Для полного описания случайной величины необходимо точно определить, какой вероятностью обладает каждое из значений, т.е. установить закон распределения случайной величины. Одной из форм закона распределения является функция распределения F(x) случайной величины x, которую иногда называют интегральной функцией распределения или интегральным законом распределения (рис. 1).
Рис. 1. График интегральной функции
С помощью графика можно определить вероятность того, что случайная величина
Функция распределения характеризуется следующими свойствами: F(x) есть неубывающая функция своего аргумента, т.е. при Другой формой закона распределения случайной величины является плотность распределения (плотность вероятности)
Плотность вероятности характеризует плотность, с которой распределяются значения случайной величины в данной точке. Функцию
Рис. 2. График плотности распределения
Плотность вероятности характеризуется следующими свойствами: плотность вероятности есть неотрицательная функция С помощью кривой распределения находится вероятность попадания случайной величины в заданные пределы. Например, вероятность попадания x на отрезок от
Из выражения (2.2) следует, что вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке (см. рис. 1). Кроме законов распределения для описания случайных величин используются числовые параметры, позволяющие в сжатой форме выразить существенные особенности распределения. В теории вероятности и математической статистике применяется большое количество различных числовых параметров. Рассмотрим лишь те из них, которые используются при исследовании точности технологических операций. Наиболее важными числовыми параметрами распределения являются параметры, характеризующие положение кривой распределения на оси абсцисс, степень рассеяния значений случайной величины, степень асимметрии и крутости кривой распределения. Из характеристик положения важнейшую роль играет математическое ожидание (среднее значение) случайной величины
Характеристикой рассеивания, разбросанности значений случайной величины около ее математического ожидания является дисперсия
Дисперсия имеет размерность квадрата случайной величины, что в практике анализа не всегда удобно. Для наглядности характеристики рассеивания удобнее пользоваться величиной среднего квадратического отклонения S, получаемой извлечением корня из дисперсии и равной
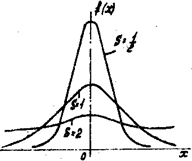
Для закона нормального распределения изменение среднего квадратического отклонения приводит к изменению формы кривой. Так как для кривой распределения расположенная под ней площадь равна единице, то изменение среднеквадратического отклонения равносильно изменению масштаба кривой распределения - увеличению масштаба по одной оси и уменьшению по другой, так, как это показано на рис. 3.
Рис.3.Кривая нормального распределения при различных значениях среднего квадратического отклонения
Распределения случайной величины могут быть симметричными и асимметричными по отношению к математическому ожиданию. Например, асимметричность распределения признака качества обрабатываемых деталей вызывается систематическими ошибками (износ и деформация инструмента, температурные деформации и т.д.). Асимметрия находится из выражения
Степень крутости, т.е. островершинности или плосковершинности кривой распределения оценивается при помощи эксцесса E, который рассчитывается по формуле
В технологии приборостроения интерес представляет не просто степень крутости кривой распределения, а ее отклонение от степени крутости образцовой кривой распределения, в качестве которой выбирается кривая нормального распределения. Для нормального распределения эксцесс равен нулю; кривые более островершинные по сравнению с нормальной обладают положительным эксцессом, кривые более плосковершинные – отрицательным эксцессом. На рис. 4 представлены нормальное распределение (кривая 1), распределение с положительным эксцессом (кривая 2) и распределение с отрицательным эксцессом (кривая 3).
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.99.221 (0.007 с.) |




 не превысит некоторого значения
не превысит некоторого значения 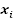 , т.е.
, т.е.
 ,
,  , на минус бесконечности функция распределения равна нулю
, на минус бесконечности функция распределения равна нулю  ; на плюс бесконечности функция распределения равна единице
; на плюс бесконечности функция распределения равна единице  .
. , которая представляет собой производную от функции распределения
, которая представляет собой производную от функции распределения


 , т.е. вся кривая распределения лежит не ниже оси абсцисс; интеграл в бесконечных пределах от плотности равен единице
, т.е. вся кривая распределения лежит не ниже оси абсцисс; интеграл в бесконечных пределах от плотности равен единице 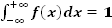 , т.е. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
, т.е. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице. до
до  равна площади кривой распределения, опирающейся на этот участок (рис.2, заштрихованная область), т.е.
равна площади кривой распределения, опирающейся на этот участок (рис.2, заштрихованная область), т.е. .
. Учитывая соотношение (2.1), вероятность попадания x в заданные пределы от
Учитывая соотношение (2.1), вероятность попадания x в заданные пределы от  .
. , указывающее некоторое среднее ориентировочное значение, около которого группируются все возможные значения случайной величины. Среднее значение случайной величины есть некоторое число, являющееся как бы ее "представителем" и заменяющее ее при грубо ориентировочных расчетах. Математическое ожидание определяется формулой вида
, указывающее некоторое среднее ориентировочное значение, около которого группируются все возможные значения случайной величины. Среднее значение случайной величины есть некоторое число, являющееся как бы ее "представителем" и заменяющее ее при грубо ориентировочных расчетах. Математическое ожидание определяется формулой вида
 .
. , которая определяется следующей формулой:
, которая определяется следующей формулой:
 .
.

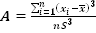 .
.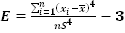 .
.


