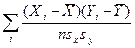Повторение отдельных фрагментов курса по теории вероятностей

 

1. Функция плотности одномерного распределения и функция распределения для одномерных непрерывных и дискретных распределений; связь этих функций друг с другом; основные параметры любого[20] одномерного распределения - математическое ожидание, мода, медиана и другие квантили, дисперсия.

2. Площадь под кривой функции плотности как оценка вероятности попадания значения случайной величины в соответствующий отрезок.

3. Выборочное представление функции плотности распределения признака (непрерывного и дискретного): частотная таблица, полигон, гистограмма (в том числе с неравными интервалами). Различие стоящих за выбором полигона и гистограммы предположений о распределении признака внутри каждого интервала. Анализ моделей, заложенных в указанных способах выборочного представления случайной величины, их различие: при использовании полигона предполагаем, что все попавшие в интервал значения сосредоточены в одной точке (важно, что при построении графика на оси х может быть выбрана любая точка интервала, т.е. что выбор такой точки – тоже модельное предположение); при использовании гистограммы считаем, что распределение в каждом интервале равномерно; гистограмму имеет смысл рассчитывать только для непрерывного признака. Проблема построения выборочной функции плотности для непрерывного признака: разбиение диапазона изменения признака на интервалы, отнесение «стыка» соседних интервалов к одному из концов, пропущенные данные. Цели заполнения пропусков. Способы такого заполнения: средним арифметическим (может быть, с учетом значений других признаков) или другими средними (с учетом шкал, о шкалах пойдет речь в лекции 2), равномерно по всем градациям, пропорционально получившимся частотам. Модели, стоящие за каждым названным подходам к заполнению пропущенных значений.

4. Выборочное представление функции распределения (кумулята): частотная таблица, полигон и гистограмма.

5. Статистики, отвечающие основным параметрам одномерного распределения: среднее арифметическое, дисперсия, мода, медиана и другие квантили. Медиану необходимо уметь считать двумя способами: как середину вариационного ряда и с помощью кумуляты. То же для других квантилей. Снова обратить внимание на модель, заложенную в методе.

 

Напомним основные формулы для расчета медианы и моды[21].

 

,

 

где х₀ – начало (нижняя граница) медианного интервала; d - величина медианного интервала; n - объем выборки (или 100%, либо 1); n_Н – частота (или относительная частота в процентах, либо в долях), накопленная до медианного интервала; n_Ме – частота (или относительная частота в процентах, либо в долях) медианного интервала.

 

,

где x₀ – начало (нижняя граница) модального интервала; d - величина модального интервала; n_Mo – частота модального интервала; n^- - частота интервала, предшествующего модальному; n⁺ - частота интервала, следующего за модальным. Частоты, как и выше, везде могут быть заменены на относительные частоты, выраженные либо в процентах, либо в долях.

 

6. Функция плотности и функция распределения двумерных случайных величин. Основной параметр двумерного распределения – коэффициент корреляции.

7. Выборочное представление функции плотности двумерной случайной величины (частотная таблица, или таблица сопряженности). Маргинальные частоты, их связь с одномерными распределениями рассматриваемых признаков. Статистика, отвечающая генеральному коэффициенту корреляции.

 

Напомним формулу для вычисления последней названной статистики.

 

 

r =

Кроме того, напомним важное свойство коэффициента корреляции: он измеряет только линейную связь. Это означает, что если он равен 1 или –1, то отвечающие нашим объектам точки рассматриваемого двумерного признакового пространства лежат на прямой линии, т.е. между признаками имеется точная линейная связь (прямая или обратная). А вот если r=0, то это означает не отсутствие связи вообще, а только отсутствие линейной связи. Нелинейная же связь при этом может быть и весьма сильной. Об этом мы будем говорить подробнее при обсуждении темы 13 (посвященной корреляционному отношению – коэффициенту, позволяющему измерить нелинейную связь).

 

8. Понятие случайной выборки. Ее построение с помощью таблицы случайных чисел.

 

Примеры задач.

 

1. Придумать пример, демонстрирующий, что при разных разбиениях диапазона изменения непрерывного признака на интервалы можно получить качественно разные полигоны распределения – выборочные представлений функции плотности (разнокачественность распределений связать с пониманием описания данных как одной из задач науки). Примеры разнокачественных распределений: одновершинное и двухвершинное, одновершинное и равномерное, равномерное и с «ямой» и т.д.

 

 

1. Задана следующая частотная таблица:

 

Возраст (лет)	15-20	20-50	50-55
Относительная частота	1/3	1/3	1/3

 

Простроить соответствующую гистограмму (заметим, что представленное в таблице разбиение диапазона изменения возраста на интервалы не лишено смысла; например, такое разбиение может явиться следствием особого внимания исследователя к тем периодам жизни человека, когда он вступает в трудовую жизнь (15-20 лет) и постепенно выходит из нее, готовясь к пенсии (5—55 лет для женщи5н).

 

1. Описать, какие модели стоит за стандартными формулами расчета моды и медианы.

 

1. Вспомнить геометрические правила расчета медианы с помощью выборочной функции распределения – кумуляты (в виде полигона). Показать, что эти правила приводят к тому же результату, что и соответствующая формула из п. 5 выше (раздел «Повторение отдельных фрагментов курса по теории вероятностей»).

 

1. Разработать такой геометрический способ расчета моды с помощью выборочной функции плотности распределения (в виде гистограммы), который отвечал бы соответствующей формуле из п.5 выше.

 

1. Составить формулы (аналогичные формуле для расчета медианы), позволяющие рассчитывать квартили, децили, процентили и другие возможные квантили. Показать, как эти формулы могут быть заменены геометрическими построениями на основе кумуляты.

 

1. Предположим, что исследователя в первую очередь интересуют те возрастные категории, которые отвечают вхождению человека в работоспособный возраст (15-10 лет) и выходу из него (50-55 лет для женщин). Тогда естественным представляется разбиение диапазона изменения возраста на интервалы, представленные в следующей таблице:

 

Возрастной интервал	15-20	20-50	50-55
Доля лиц, попавших в интервал	1/3	1/3	1/3

 

Построить гистограмму, отвечающую отраженным в таблице данным. Обосновать теоретически выбранный способ построения.

 

1. Рассчитать средние и дисперсию для доли явившихся на голосование жителей некоторого региона, если известны аналогичные доли для каждого из находящихся на территории региона участков. Данные представлены следующей таблицей:

 

 

Доля явившихся на голосование	10 – 20	20 – 30	30 – 40
Количество избирательных участков

 

 

1. Рассчитать коэффициент корреляции между стажем работника и его зарплатой на основе следующей частотной таблицы

 

Зарплата (в т.р.)	Стаж (в годах)
1-5	5-10	10-15	Нет ответа
0,5 – 1,5
1,5 – 2,5
2,5 – 3,5

 

1. У 12 школьников изучались две характеристики: оценки IQ, определенные с помощью шкалы интеллекта Стенфорда-Бине в шестом классе (Х) и успеваемость по химии в средней школе, оцененная на основе теста, состоящего из 35 вопросов (Y). Полученные данные отражены в следующей таблице:

 

N 1 2 3 4 5 6 7 8 9 10 11 12

X 120 112 110 120 103 126 113 114 106 108 128 109

Y 31 25 19 24 17 28 18 20 16 15 27 19

 

Рассчитать коэффициент корреляции между Х и Y.

 

1. Показать, каким образом связаны выборочные формулы для расчета статистик: среднего арифметического, дисперсии, коэффициента корреляции для непрерывного признака – и известные формулы для расчета (с помощью интегралов) отвечающих этим статистикам генеральных параметров: математического ожидания, дисперсии, коэффициента корреляции.

 

1. Показать, как выглядит функция плотности равномерного распределения и каким образом из нее с помощью интегрирования можно получить соответствующую функцию распределения. Как последняя выглядит?

 

1. Осуществить с помощью таблицы случайных чисел выбор 5-ти студентов из группы.

 

 

Добавочная литература к теме 1.

Обязательная

(для повторения материала из курса по теории вероятностей: расчет выборочных статистик, отвечающих известным параметрам генеральных распределений)

Толстова Ю.Н. Анализ социологических данных: методология, дескриптивная статистика, изучение связей между номинальными признаками. М.: Научный мир, 2000

 

Ниворожкина Л.И., Морозова З.А. Основы статистики с элементами теории вероятностей. Для экономистов. Ростов-на-Дону: Феникс, 1999

 

Рабочая книга социолога. М.: Наука, 1983

 

 

Дополнительная

О методологических принципах использования математики в социологии

Толстова Ю.Н. Методология математического анализа данных // Толстова Ю.Н. Социология и математика. М.: Научный мир, 2003. С.80-94. А также: СОЦИС, 1990, №6, с. 77-87.

Проблемы пропущенных данных в массовых опросах

Алгоритмы и программы восстановления зависимостей. - М.: Наука, 1984.

Вапник В.Н. Восстановление зависимостей по эмпирическим данным. - М.: Наука, 1979.

Загоруйко Н.Г. Эмпирическое предсказание. - Новосибирск: Наука, 1979. С. 105-118.

Клюшина Н.А. Причины, вызывающие отказ от ответа // Социс (Социологические исследования). - 1990. - N1. С. 98-105.

Лакутин О.В. Учёт пропущенных данных / Применение математических методов и ЭВМ в социологических исследованиях. - М.: ИСИ АН СССР, 1982. С.86-90.

Лбов Г.С. Методы обработки разнотипных экспериментальных данных. - Новосибирск: Наука, 1981. С. 38-41, 52-55.

Литтл Р.Дж., Рубин Д.Б. Статистический анализ данных с пропусками. - М.: Финансы и статистика, 1991.

Фёдоров И.В. Причины пропуска ответа при анкетном опросе // Социс. - 1982. - N 2.

Проблемы разбиения диапазона изменения признака на интервалы

Орлов А.И. Асимптотика квантований и выбор числа градаций в социологических анкетах / Математические методы и модели в социологии. - М.: ИСИ АН СССР, 1977. С.42-55.

Пасхавер Б. Проблема интервалов в группировках // Вестник статистики. - 1972. - N 6.

Сиськов В.И. Об определении величины интервалов при группировках // Вестник статистики. - 1971. - N 12.

А.А.Чупров. О приемах группировки статистических наблюдений // Известия Санкт-Петербургского политехнического института. 1904. Т. 1. Вып. 1–2.

Doane D.P. Aesthetic frequency classification. American Statistician, 30, 1976. P. 181-183.

Freedman D., Diaconis P. On this histogram as a density estimator: L₂ theory. Zeit. Wahr. Ver. Geb.,57, 1981. P.453-476.

Scott D.W. On optimal and data-based histograms. Biometrika, 66, 1979. P. 605-610.

Scott D.W. Multivariate density estimation: theory, practice, and visualization. N.-Y.: John Wiley & Sons, 1992.

Sturges H. The choice of a class-interval. J.Amer. Statist. Assoc., 21, 1926. P.65-66.

Wand M.P. Data-based choice of histogram bin-width. Technical report, Australian Graduate Scool of management, university of NSW. 1995.

 

ТЕМА 2.