
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухфакторный дисперсионный анализ.Содержание книги
Поиск на нашем сайте
15.1. Двухфакторный дисперсионный анализ как метод анализа результатов эксперимента при изучении причинно-следственных отношений
Предположим, что решая рассмотренную выше задачу - выявление зависимости (независимости) успехов студентов от формы обучения, мы пришли к выводу о неполноте такой постановки задачи: к примеру, поняли, что эффективность формы обучения зависит от пола студента. Исходная матрица ячеек становится двумерной. Покажем, как она строится. Пусть величина Yijk означает значение главного интересующего нас признака Y, вычисленное для i-го по счету (счет ведется внутри ячейки) объекта, помещенного в ячейку с номером (j, k), где j – отвечающее рассматриваемой ячейке значение первого фактора X1 , а k – отвечающее той же ячейке значение второго фактора X2 . Будем рассматривать упрощенный случай, когда число объектов во всех ячейках одинаково и равно n (в приведенной ниже таблице n = 3). Фактор X1 - значения 1, 2, …, J (в примере J=2), а фактор X2 принимает значения 1, 2, …, K (в нашем примере K = 3).
6.1. Модель двухфакторного дисперсионного анализа
Общая модель двухфакторного дисперсионного анализа имеет вид:
где - - - - - eI j k – поправочный коэффициент (остаточный член), говорящий о различии между реальным значением Y-ка для рассматриваемого респондента и тем его значением, которое должно получиться для любого респондента, вошедшего в рассматриваемую ячейку (с номером (j,k)) в соответствии с нашей моделью. Особое внимание стоит уделить понятию взаимодействия. Именно наличием этого элемента принципиально отличается двухфакторный дисперсионный анализ от однофакторного. Наличие взаимодействия двух признаков (в отношении некоторого зависимого признака Y) говорит о том, что вид связи первого признака с Y зависит от того, какое значение принимает второй признак. К примеру, по отдельности и форма обучения, и пол могут в среднем (статистически) не влиять на качество обучения, но, скажем, вторая форма обучения применительно к девушкам при этом может давать очень высокий положительный эффект. Другими словами, действие формы обучения зависит от того, для девушек или для юношей она используется. Когда в принципе уровень Y-ка зависит от сочетаний конкретных значений X1 и X2, говорят о наличии взаимодействия между рассматриваемыми факторами. Иногда в том же смысле говорят о синергетическом эффекте, вызванном сочетанием значений факторов. В том же смысле ведут речь о нелинейности воздействия факторов на зависимую переменную. Иногда взаимодействием называют само сочетание значений факторов, обусловливающее некий конкретный уровень Y-ка.[101]
Выборочные оценки всех формирующих модель составляющих вычисляются аналогично тому, как это делалось для однофакторного дисперсионного анализа.
Определенную сложность представляет лишь оценка взаимодействия. Зададимся вопросом о том, каким образом можно оценить наличие (или отсутствие) взаимодействия в конкретной ячейке с номером (j,k). Наличие некоего среднего уровня, совокупное воздействие j-го уровня фактора X1 и k-го уровня фактора X2 в отдельности вкупе с взаимодействием указанных уровней приводят к тому, что средний уровень успеваемости для объектов рассматриваемой ячейки оказывается равным
Аналогичные рассуждения справедливы и для генеральной совокупности. Этим мы воспользуемся в следующем параграфе при обсуждении вида гипотез, проверяемых в двухфакторном дисперсионном анализе.
15.3. Двухфакторный дисперсионный анализ как проверка статистических гипотез В двухфакторном дисперсионном анализе проверяются три статистические гипотезы. Первые две аналогичны гипотезе однофакторного анализа, это гипотезы: H0: m·1· = m·2· = … = m·J· (15.2) H0: m··1 = m··2 = … = m··K. (15.3)
При проверке первой гипотезы мы как бы забываем о втором факторе и рассматриваем J ячеек, на которые наша совокупность делится в соответствии со значениями первого фактора. При проверке второй гипотезы аналогичные рассуждения используем применительно ко второму фактору. Использующиеся критерии очень похожи на те, которые фигурируют в однофакторном дисперсионном анализе (отличие состоит в виде внутригрупповой дисперсии, что станет ясно из приведенных ниже формул). Третья гипотеза говорит об отсутствии взаимодействий, или, что то же самое, о равенстве всех взаимодействий нулю. В соответствии с формулой (15.1), речь идет о проверке равенства нулю выражений вида m·jk - m·j· - m··k + m···. Известно, что можно говорить о равенстве нулю всех чисел из некоторой совокупности, если сумма квадратов этих чисел равна нулю. Поэтому третья проверяемая в двухфакторном дисперсионном анализе гипотеза имеет вид: H0 : Перейдем к обсуждению вида критериев, использующихся для проверки указанных трех гипотез. Вместо межгрупповой суммы квадратов, обозначенной нами выше SSb = SSмежду, введем в рассмотрение три аналогичные суммы: SS1, SS2, SS12, отвечающие, соответственно, гипотезам (15.2), (15.3), (15.4).
SS1 = nK
Внутригрупповая сумма квадратов SSw = SSвнутри вычисляется одинаковым образом для всех трех гипотез:
SSw =
Каждой сумме квадратов отвечает свое число степеней свободы: df 1 = J-1; df 2= K-1; df 12 = (J-1)(K-1); df w = JKn – JK;
Введем обозначения средних квадратов: MS1 = SS1 / df 1 ; MS2 = SS2 / df2 ; MS12 = SS12 / df 12 ; MSw = SSw/ df w. Искомые статистики имеют вид:
Логика проверки соответствующих гипотез – та же, к которой читатель, как мы надеемся, уже привык. В заключение обсуждения вопроса о дисперсионном анализа отметим, что существуют такие его варианты, которые рассчитаны на порядковые данные (непараметрический дисперсионный анализ).
Примеры задач 1. Исcледователи решили выяснить, в какой мере крепость семьи связана с тем, одинаковы или нет национальности супругов, и каково количество детей в семье. Для ряда семей по определенной методике был рассчитан коэффициент прочности семьи (число от 1 до 10). Наблюдаемые данные были сведены в следующую таблицу (в клетках – коэффициенты прочности обследованных семей).
Что можно сказать о влиянии названных факторов на крепость семьи? Добавочная литература к главам 14 и 15 [102] Основная Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998. С.349-362 (однофакторный дисперсионный анализ) Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. Ростов-на-Дону: Феникс, 2005. С.207-239 (однофакторный, двухфакторный, трехфакторный дисперсионный анализ) Калинина В.Н., Панкин В.Ф. Математическая статистика. М.: Высшая школа, 1998. С. 244-266 (однофакторный и двухфакторный дисперсионный анализ) Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика, М.: Инфра-М,1997.С. 184-191; Юнити, 2003 (однофакторный и двухфакторный дисперсионный анализ) Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ-ДАНА, 2001. С.375-391 (однофакторный и двухфакторный дисперсионный анализ) Дополнительная Гусев А.Н. Дисперсионный анализ в экспериментальной психологии: Учебное пособие для студентов факультетов психологии ВУЗов по направлению 512000 – «Психология», М.: Учебно-методический коллектор «Психология», 2000 Крыштановский А.О. Анализ социологических данных с помощью пакета SPSS.М.:Издательский дом ГУ-ВШЭ, 2005. С. 109-114 (непараметрический дисперсионный анализ Краскэла – Уоллиса) Сидоренко Е. Методы математической обработки в психологии. СПб: Речь, 2000. С. 224-260 (однофакторный и двух факторный дисперсионный анализ) Статистические методы анализа социологической информации. М.: Наука, 1979. Гл. 11. Girden E.R. ANOVA: Repeated measures // Sage University Paper series on Quantitative applications in the social sciences; Beverly Hills: SAGE Publications. V. 84.
СМ 1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. Учебник для вузов. – М.: ЮНИТИ, 1998. С. 282-319. 2. Крыштановский А.О. Анализ социологических данных с помощью пакета SPSS. Издательский дом ГУ-ВШЭ. Москва, 2006. 3. Эддоус М., Стэнсфилд Р. Методы принятия решений/ Пер. с англ. Под ред. Член-корр. РАН И.И.Елисеевой. – М.: Аудит, ЮНИТИ, 1997. 4. Руководство пользователя SPSS 11.0. 5. Бююль А., Цефель П. SPSS: искусство обработки информации, анализ статистических данных и восстановление скрытых закономерностей. DiaSoft, 2002.
Приложение 1 Литература Основная Андропов А.М., Копытов Е.А., Гринглаз Л.Я. Теория вероятностей и математическая статистика. Учебник для вузов. С.-Пб: Питер, 2004 Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. С.-Пб: Лань, 2004 Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998 Гмурман В.Е. Руководство к решению задач по теории вероятностей математической статистике. М.: Высшая школа, 1998 Калинина В.Н., Панкин В.Ф. Математическая статистика. М.: Высшая школа, 1998 Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика, М.: Инфра-М,1997; Юнити, 2003 Кочетков Е.С., Смерчинская С.О., Соколов В.В. Теория вероятностей и математическая статистика. М.: Изд. дом «Форум», 2003 Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ-ДАНА, 2001 Прикладная статистика. Основы эконометрики. Т.1: Айвазян С.А., Мхитарян В.С. Теория вероятностей и прикладная статистика. М.: Юнити-Дана, 2001 Теория статистики с основами теории вероятностей / Под ред. И.И.Елисеевой. М.: Юнити, 2001 Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере. М.: ИНФРА-М, 2003 Шведов А.С. Теория вероятностей и математическая статистика. М.: Изд. дом ГУ-ВШЭ, 2005
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 665; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.204 (0.01 с.) |


 ·2· =5,6
·2· =5,6
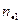 =nJ=3·2=6
=nJ=3·2=6

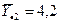
 ,
, - значение зависимого признака для конкретного респондента, помещенного в ячейку, отвечающую j – му уровню первого фактора и k – му уровню второго фактора (скажем, обучающемуся по второй форме юноши, тогда j=2, k=1), имеющему номер i в соответствующей ячейке;
- значение зависимого признака для конкретного респондента, помещенного в ячейку, отвечающую j – му уровню первого фактора и k – му уровню второго фактора (скажем, обучающемуся по второй форме юноши, тогда j=2, k=1), имеющему номер i в соответствующей ячейке; - вклад j-го уровня (нижний индекс) первого фактора (верхний индекс) X1 в формирование значения Y (в нашем примере первый фактор – форма обучения; упомянутый вклад определяется тем, что студент обучался либо по первой форме обучения (j=1), либо по второй (j=2), либо по третьей (j=3));
- вклад j-го уровня (нижний индекс) первого фактора (верхний индекс) X1 в формирование значения Y (в нашем примере первый фактор – форма обучения; упомянутый вклад определяется тем, что студент обучался либо по первой форме обучения (j=1), либо по второй (j=2), либо по третьей (j=3)); - вклад k-го уровня второго фактора X2 в формирование значения Y (в нашем примере второй фактор – пол студента; соответствующий вклад определяется тем, является ли студент юношей или девушкой);
- вклад k-го уровня второго фактора X2 в формирование значения Y (в нашем примере второй фактор – пол студента; соответствующий вклад определяется тем, является ли студент юношей или девушкой); - вклад, определяющийся взаимодействием i-го уровня первого фактора и j-го уровня второго;
- вклад, определяющийся взаимодействием i-го уровня первого фактора и j-го уровня второго; ···
···
 (m·jk - m·j· - m··k + m···)2 = 0. (15.4)
(m·jk - m·j· - m··k + m···)2 = 0. (15.4) (
( (
( (
( (
( ;
;  ;
;  .
.


