Модель однофакторного дисперсионного анализа

 

Прежде, чем говорить о строгом способе решения поставленной задачи, необходимо четко описать ту модель, которая лежит в основе всех формальных построений. Модель кажется очень простой. Но далее, перейдя к рассмотрению двухфакторного дисперсионного анализа, мы увидим, что подобные модели могут быть гораздо более сложными и неочевидными. Научиться же строить подобные модели надо. Причин тому, по крайней мере, две.

Во-первых, подобного рода модели используются очень часто: в регрессионном, логлинейном и других видах анализа данных. И их смысл надо хорошо понять, чтобы иметь возможность читать соответствующую литературу.

Во-вторых, хорошее понимание смысла подобных моделей, на наш взгляд, может способствовать усвоению очень актуального методологического принципа - прежде, чем собирать данные, необходимо сформировать систему «аксиом», четко обрисовывающих априорное представление социолога о том, что он изучает. При всей своей очевидности это положение на практике часто не выполняется. В результате используются анкеты, в которые включены вопросы, не имеющие отношения к делу, не включены необходимые вопросы и т.д.

Все методы анализа данных опираются на такие априорные аксиомы. Они и составляют суть модели, заложенной в том или ином методе. Привычка пользоваться методами, как нам представляется, должна способствовать выработке состоятельного с методологической точки зрения подхода к планированию социологического исследования. Или, коротко говоря, – математика может научить социолога методологической грамотности.

В данном случае имеется в виду одна «аксиома» – четкая формулировка того, отчего зависит основной интересующий исследователя признак Y. Предположение о том, из чего для каждого конкретного респондента формируется уровень признака Y, выглядит следующим образом:

,

где - некий средний уровень, на фоне которого изучается действие фактора Х на признак Y; 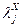- это вклад в формирование значения зависимого признака j - го уровня фактора Х; 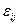- добавка, отражающая специфические характеристики именно того (неповторимого) респондента, который включен в j-ю ячейку и имеет в ней номер i.

Сделаем несколько замечаний по поводу отдельных членов модели.

Сущность поясним на примере: наверное, этот уровень будет один для выпускников московских школ, другой – для выпускников деревенских школ Иркутской области и третий – для молодежи Центрально-африканской республики. Модель действительна на генеральной совокупности. Выборочной оценкой среднего уровня служит .

По поводу можно сказать, что это – главный интересующий нас элемент, центральное звено модели. Размер именно этой величины и говорит о том, насколько j-я форма обучения детерминирует уровень полученных студентом знаний. Выборочной оценкой этого показателя служит разность .

- это некоторый поправочный элемент, корректирующий основную часть модели, выраженную суммой ( + ). Коррекция требуется потому, что, как бы хорошо ни моделировалась величина этой суммой (а мы ищем именно такой фактор, чтобы равенство = ( + ) по возможности отражало реальность), последняя никогда не сможет учесть все специфические особенности отдельных людей. Точным равенство = ( + ) не будет никогда. Но мы все же будем считать его приемлемым, если величины в среднем равны нулю, независимы и как бы погашают друг друга. К примеру, если у i-го респондента из j-й группы окажется большим по абсолютной величине и отрицательным (из-за того, что этот респондент, к примеру, много болел в течение того года, когда проводился эксперимент; это привело к тому, что успехи студента оказались ниже, чем следовало бы ожидать при рассматриваемом среднем уровне и воздействии соответствующей формы обучения), то в той же группе найдется такой k –й респондент, у которого будет примерно таким же по модулю, но положительным (из-за того, скажем, что этот респондент весь год усиленно занимался дополнительно с преподавателем). Обычно предполагается, что величины имеют нормальное распределение с нулевым математическим ожиданием.

Если же окажется, что довольно велики и практически у всех респондентов положительны, - значит, мы не учли действие какого-то общего для всех респондентов фактора. И нам надо или заменить фактор Х другим, или перейти к двухфакторному дисперсионному анализу. Величины называются остатками, и математическая статистика обычно представляет исследователю средства проанализироваать эти остатки (это имеет место не только для дисперсионного анализа).

Выборочной оценкой величины служит разность .

 

Все три элемента модели могут быть расценены как вклады в вариацию признака Y, как источники такой вариации.