
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методологические аспекты проверки математико-статистических гипотезСодержание книги
Поиск на нашем сайте 11.1. Ошибки первого и второго рода. Надеемся, читателю ясно, что принятие решения на основе проверки той или иной математико-статистической гипотезы H0 носит вероятностный характер. Мы можем совершить две ошибки: отвергнуть верную гипотезу и принять неверную. Какова вероятность каждой из этих ошибок? Как уменьшить эти вероятности? Попытаемся ответить на эти вопросы. Прежде всего напомним, что если значение используемого критерия попало в «маловероятную» область (т.е. «зашкалило» за соответствующее критическое, табличное значение, вероятность чего мала при справедливости H0, меньше выбранного нами уровня значимости a), гипотеза отвергается. Но ведь наш уровень значимости не равен нулю. Пусть очень редко, но значение критерия для конкретной выборки все же может «зашкалить» за найденное нами критическое значение и при справедливости H0. Тогда отказ от H0 будет ошибкой: гипотеза верна, а мы ее отвергли. Эта ошибка называется ошибкой первого рода. Представляется очевидным, что вероятность совершения такой ошибки равна a. Ясно, что мы можем этой вероятностью управлять. Если для нас из содержательных соображений является важным недопущение отказа от справедливой гипотезы, будем уменьшать значение a и, соответственно, увеличивать критическое значение критерия. А в каких случаях мы можем принять в действительности неверную гипотезу, т.е. совершить ошибку второго рода? Чтобы разобраться с этим, введем понятие мощности критерия и поясним, что это такое, на примере. Рассмотрим один из возможных способов проверки затронутой нами в п. 10.3 гипотезы H0: r = 0. В качестве альтернативной рассмотрим гипотезу H1: r ¹ 0. Ясно, что эта гипотеза – не направленная и поэтому критерий будет двусторонним. Поэтому при a = 0,05 табличное значение будем считать для Обратимся к рисунку 11.1. Известно, что если в генеральной совокупности (для приводимых ниже рассуждений требуется, чтобы нашим признакам отвечало двумерное нормальное распределение) коэффициент корреляции равен нулю (т.е. если наша нуль-гипотеза верна), то всевозможные выборочные значения этого коэффициента для выборки объема n будут иметь приблизительно нормальное распределение с нулевым средним и стандартным отклонением, равным
Рис. 11.1. Пример мощности критерия для H0: r = 0 против H1: r ¹ 0 в случае, когда r = 0,20 (n =200, a = 0,05)[61]; r = rвыб.
этого распределения, равная 0,025, будет находиться правее величины r = 0,14 (соответствующее табличное значение, равное, как известно 1, 96, будучи умноженным на среднее квадратическое отклонение, равное 0,071, даст как раз 0, 14). Значит, в соответствии с неоднократно описанной ранее логикой проверки статистических гипотез, мы будет отклонять нашу H0, если А теперь представим себе, что в действительности в генеральной совокупности коэффициент корреляции равен не нулю, а, скажем, 0,2. Тогда распределение выборочных коэффициентов корреляции будет совпадать с правой кривой, представленной на рассматриваемом рисунке (соответствующее sr будет несколько меньше, чем у левой кривой, но на этом мы останавливаться не будем). Мы об этом не знаем и продолжаем использовать обычную логику принятия или отвержения гипотезы. Естественно, если в такой ситуации мы примем нашу гипотезу, то тем самым совершим ошибку второго рода. В соответствии с нашими правилами, мы именно таким образом ошибемся, если наш единственный выборочный коэффициент корреляции попадет в интервал от –0,14 до + 0,14. Чтобы оценить вероятность этой ошибки, ошибки второго рода, вспомним, что в действительности распределение выборочных средних совпадает с правой кривой рисунка 11.1. И вероятность попадания нашего единственного выборочного значения коэффициента корреляции будет равна соответствующей площади под этой самой правой кривой. На рисунке она помечена буквой b. Это и есть вероятность ошибки второго рода. Мы видим, что она не очень велика. Это означает, что довольно большой является величина (1-b). Она называется мощностью критерия. На рис. 11.1 мощность критерия равна заштрихованной площади и составляет примерно 0,82. Таким образом, для того, чтобы вероятность ошибки второго рода была мала, необходимо, чтобы мощность критерия была велика. Ясно, что мощность критерия равна вероятности отвергнуть неверную нуль-гипотезу. Чтобы более ярко представить себе, что такое мощность критерия, предположим, что в реальности генеральное значение нашего коэффициента корреляции равно 0,1. Тогда ситуация, подобная только что рассмотренной, будет иметь вид, представленный на рис. 11.2.
Рис. 11.2. Пример мощности критерия для H0: r = 0 против H1: r ¹ 0 в случае, когда r = 0,10 (n =200, a = 0,05)[62].
Как и выше, мы принимаем нашу нуль гипотезу (и тем самым совершаем ошибку второго рода, если наш единственный выборочный коэффициент попадет в интервал от –0,14 до +0,14. Фактическая вероятность этого равна заштрихованной площади под правой кривой на рис. 11.2 (ведь в действительности именно эта кривая отвечает распределению выборочных значений коэффициентов корреляции). b, равная вероятности совершения ошибки второго рода, велика. Мощность критерия, равная (1-b), мала.
Рис. 11.3. Кривая мощности для критерия для H0: r = 0 против H1: r ¹ 0 при n =200 и a = 0,05 [63].
Рассмотрим график на рис. 11.3. По горизонтали откладываются значений генеральных коэффициентов корреляции. По вертикали – вероятность отвергнуть неверную нуль-гипотезу, т.е. мощность критерия. Надеемся, что читателю понятен смысл этой кривой. Если в генеральной совокупности коэффициент корреляции близок к нулю, то у нас будет очень мала вероятность отвергнуть нашу нулевую гипотезу (эта вероятность будет равна выбранному уровню значимости). Это означает, что мощность критерия мала: велика величина b, т.е. вероятность принятия H0. Если же генеральный коэффициент корреляции достигает 0,3 и выше, то у нас вероятность отвержения нуль-гипотезы становится близкой к 1.
Все сказанное в этом параграфе можно свести в следующую таблицу.
a - уровень значимости, (1 - b) - мощность критерия.
11.2. Пример влияния содержательного характера задачи на выбор уровня значимости. Выше мы говорили о том, что на выбор уровня значимости при проверке гипотез может влиять содержательный характер решаемой задачи. Приведем пример того, когда это имеет место применительно к проверке об отсутствии связи на основе критерия Хи-квадрат. Приведем пример гипотетической задачи. Предположим, что руководитель некоторого региона должен принять решение по вопросу о том, стоит или не стоит осушать имеющиеся в этом регионе болота. Если между заболоченностью почвы в регионе и уровнем заболеваемости его жителей есть связь, то необходимо затрачивать огромные средства на осушение болот. Если связи нет – средства можно не тратить. А денег мало… В таком случае для руководителя естественным будет стремление уменьшить ту область, где он может совершить ошибку первого рода – отвергнуть в действительности верную гипотезу, т.е. уменьшить a - вероятность отвержения справедливой гипотезы. Будем полагать, например, что свершение события, имевшего вероятность 0,05, еще не говорит о несправедливости наших посылок – вероятность, конечно, мала, но все же довольно существенна и можно полагать, что все же в генеральной совокупности связи нет (гипотеза верна). Может быть, и относительно вероятности 0,01 мы также будем рассуждать. А вот если мы встретим событие, вероятность реализации которого в предположении справедливости нуль-гипотезы была равна 0,001, тут уж мы засомневаемся. Наверное, такое событие не может реализоваться. Значит, действительная вероятность свершившегося события (отклонения выборочной частотной таблицы от ситуации пропорциональности) была не столь ничтожной. Другими словами, в генеральной совокупности столбцы (строки) таблицы, всего вероятнее, - не пропорциональны, т.е. между переменными имеется связь. Придется раскошеливаться на мелиорацию земель. То, что обычно принимается соотношение a = 0,05, опирается на большой практический опыт. В подавляющем числе реальных задач предположение о том, что события с такой вероятностью практически не случаются, вполне оправдано. Но еще раз подчеркнем, что и при проверке математико-статистических гипотез мы должны учитывать житейскую логику. Если речь будет идти, скажем, о том, что вероятность заболевания у нас горла после того, как мы съедим зимой на улице мороженое, равна 0,05, мы, наверное, предположим, что событие с такой вероятностью случиться не может, никаких неприятностей не произойдет, и смело будем потреблять мороженое. Однако в другой ситуации, скажем, если бы мы находились на месте архитектора, думающего о том, стоит ли при строительстве дома использовать сейсмостойкие конструкции, мы бы, вероятно, рассуждали по-другому. Если бы было известно, что вероятность землетрясения в рассматриваемом районе – 0,05, то мы бы, вероятно, поосторожничали, сочли бы землетрясение все же возможным и не стали бы рисковать человеческими жизнями, заложили бы в проект дорогостоящие сейсмостойкие элементы. Вот если бы наш архитектор работал в другом районе, где вероятность землетрясения - 0, 0001, то он, наверное, позволил бы себе считать, что такое событие практически произойти не может, и не стал бы делать дом сейсмостойким, сэкономив тем самым средства. Если же тяжелые для нас затраты (любого плана – материальные, моральные и т.д.) связаны с ситуацией отсутствия связи, то мы будем «бояться» совершить ошибку второго рода – придти к выводу об отсутствии связи в то время как она в действительности имеет место. В таком случае мы должны стремится увеличить мощность используемого критерия. Можно также уменьшить ту область, где гипотеза принимается, т.е. увеличить уровень значимости (тем самым мы увеличим мощность критерия). Будем полагать, что не может произойти событие, имеющее вероятность не только 0,05, но и 0,1 (a = 0,1) и будем отвергать гипотезу о независимости, если наш критерий достигнет соответствующей критической величины. А вот если встретим событие, вероятность реализации которого в предположении справедливости нуль-гипотезы была равна 0,2 - то ничего необычного в этом не найдем, т.е. будем считать, что у нас нет оснований отвергать нуль- гипотезу. И уж здесь придется идти на жертвы. Логика, прямо скажем, не очень надежная, поскольку ее реализация резко повышает вероятность ошибки первого рода – отказа от верной гипотезы. 11.3. Различие между статистической и содержательной гипотезой
Распространенным ответом студента на вопрос о том, какую математико-статистическую гипотезу надо проверить при решении той или иной конкретной задачи является фраза типа: «Надо проверить гипотезу о том, есть связь или нет». Такого рода предложение некорректно по крайней мере по двум причинам. Во-первых, сформулированная фраза вообще не содержит формулировку какой бы то ни было гипотезы. Гипотезой может быть или утверждение о том, что связь есть, или – о том, что связи нет. Во-вторых, даже гипотеза типа «здесь связь есть» может восприниматься как некоторое нечетко выраженное содержательное предположение (и как таковое имеющее право на существование), но никак не математико-статистическая гипотеза. Последняя должна быть сформулирована очень строго, например, так: «коэффициент корреляции в изучаемой генеральной совокупности равен 0,7». Именно такой строгий характер носили все рассмотренные нами выше гипотезы, обозначаемые знаком H0. В п. 7.3 мы позволяли себе выражение «H0: связи нет» только потому, что показали, что словосочетание «связи нет» может быть выражено формально, строго, на языке определенных формул (стоящих, например, за соотношениями (7.1)).. И мы не делали этого только из соображений краткости записи и стремления сделать текст более понятным для читателя-гуманитария. Формулируя строгую математико-статистическую гипотезу, мы должны также понимать, что она должна опираться на определенные математические результаты, лежащие в основе разработки используемого для проверки гипотезы критерия. Другими словами, мы должны знать, что критерий для проверки нашей гипотезы существует. И если мы с помощью математической статистики хотим проверить какую-то интересующую нас из содержательных соображений гипотезу, то сначала мы должны погрузиться в математико-статистическую литературу, в справочники и убедиться, что критерий для проверки нашей гипотезы действительно существует. Особенно осторожно надо относиться к т.н. методам анализа данных. В методах анализа данных часто используются такие математические конструкты, для которых не разработаны способы переноса результатов с выборки на генеральную совокупность (подобные методам проверки статистических гипотез и построения доверительных интервалов). Таковы, например, многие методы кластерного анализа или многомерного шкалирования. Более того, как мы уже отмечали выше (п.1.3), при анализе данных зачастую возникают такие ситуации, когда мы не можем мыслить наблюдаемые объекты как выборку из некоторой генеральной совокупности. Это может иметь место, например, в силу того, что исследователю совершенно неясно, какой в его случае является генеральная совокупность. Возможны и другие причины, например, отсутствие оснований считать значения какого-то признака реализациями одной и той же случайной величины (скажем, у нас могут быть основания считать различными распределения зарплат мужчин и женщин; а, может быть, у русских и украинцев? А, может, у «либералов» и «коммунистов»?). Заранее сказать, так это или не так, невозможно. Какие категории объектов надо «испытывать» с целью выявления специфических распределений, неясно[64]. Об использовании математической статистики, основным объектом которой являются случайные величины, говорить в такой ситуации нельзя. Стало быть, нельзя говорить и о проверке математико-статистических гипотез. О содержательных же гипотезах в принципе может идти речь. Различие между содержательными и математико-статистическими гипотезами имеет еще один очень важный для социолога аспект. Одна и та же содержательная гипотеза может быть проверена с помощью разных математико-статистических подходов. Приведем пример. Допустим, мы хотим выяснить, имеется ли статистическая связь между двумя признаками x и y, измеренными по интервальной шкале. Содержательная гипотеза может звучать, например, так: «связь между данными признаками существует»[65]. С помощью математической статистики проверку такой гипотезы можно осуществить несколькими способами, приводящими, вообще говоря, к разным результатам. Во-первых, можно вычислить коэффициент корреляции и проверить гипотезу о его равенстве нулю. Во-вторых, можно разбить диапазоны изменения значений обоих признаков на интервалы и применить критерий «Хи-квадрат». Здесь очень важно обратить внимание на то, что результат, вообще говоря, будет зависеть от способа упомянутого разбиения. При одном разбиении гипотеза об отсутствии связи может быть принята, при другом – нет. Здесь мы снова возвращаемся к одной из основных проблем математической социологии: построению признаков, отражающих то или иное социальное явление (ср. конец п. 7.3). В-третьих, можно вычислить корреляционное отношение – коэффициент, отражающий криволинейную зависимость y от x, либо x от y и проверять значимость его отличия от нуля (см. тему 13). В-четвертых, можно искать регрессионную зависимость среднего значения y от x и обосновывать статистическую значимость всех используемых при этом коэффициентов (в настоящем курсе изучение соответствующей темы не предусмотрено[66], однако регрессионный анализ описывается в очень большом количестве работ по математической статистике и анализу данных; и почти везде указываются способы статистической оценки всех получаемых при этом параметров). В-пятых, можно разбить диапазон изменения x на группы (ячейки) и применить дисперсионный анализ для сравнения значений y для объектов, попавших в разные группы (см. тему 14). Мы перечислили отнюдь не все известные способы изучения статистических связей между двумя переменными. Коснулись только самых популярных. И уже стало ясно, что множественность методов, решающих одну и ту же задачу – это проблема для социолога. Как же ее решать? Мы уже говорили в конце п.7.3, что наше знание будет объективным только в том случае, если мы наряду со сведениями, полученными в результате того или иного анализа статистических данных, в понятие «знание» будем включать также и тот способ, с помощью которого эти сведения получены. В данном случае речь идет по существу об учете той модели изучаемого явления (т.е. о том понимании статистической связи, или, может быть, причины), которая заложена в используемом нами методе (о важности учета такой модели как об одном из главных принципов использования математического аппарата в социологии шла речь в п. 1.7). Так, не имеет смысла говорить о том, что наша содержательная гипотеза о наличии связи между x и y подтвердилась. Полученный результат надо формулировать по-другому, например, так: на таком-то уровне значимости мы отвергли гипотезу о равенстве нулю коэффициента корреляции между рассматриваемыми признаками; на таком-то уровне значимости и при таком-то разбиении значений признаков на интервалы мы отвергли гипотезу об отсутствии связи с помощью критерия «Хи-квадрат», но приняли аналогичную гипотезу при некотором другом разбиении и т.д. Содержательно проинтерпретировать подобные факты можно только при том условии, что социолог достаточно хорошо представляет себе модель, заложенную в каждом методе. Надеемся, что сказанное говорит и о роли учета модели, заложенной в используемом математическом методе, и о различии между содержательной и математико-статистической гипотезами. Мы показали, что одна и та же содержательная гипотеза может проверяться с помощью использования разных математико-статистических приемов (в том числе с помощью проверки разных математико-статистических гипотез, что в основном и интересует нас в настоящем параграфе). Можно показать и обратное утверждение: даже при рассмотрении одних и тех данных проверка одной и той же математико-статистической гипотезы может быть использована для решения разных содержательных задач, для проверки разных содержательных гипотез. Приведем пример. Вспомним гипотезу H0: m1 = m2. И вспомним уже упоминавшуюся задачу сравнения средних зарплат для мужчин и для женщин. Вопрос, на который мы намереваемся получить ответ с помощью проверки рассматриваемой гипотезы, может формулироваться по-разному, например: можно ли считать, что различие между средними зарплатами мужчин и женщин статистически значима? Можно ли полагать, что зарплата детерминируется полом? Первый вопрос может быть одним из многих других вопросов: о различии заплат у лиц разных национальностей, разных профессий и т.д. А второй может отражать работу специалиста по гендерной социологии о дискриминации женщин. Хотя задачи и схожи, но все же содержательные гипотезы здесь будут разными.
Раздел IY. ПРОБЛЕМА ИЗУЧЕНИЯ ПРИЧИННО-СЛЕДСТВЕННЫХ ОТНОШЕНИЙ И ЭКСПЕРИМЕНТ В СОЦИОЛОГИИ; ОСНОВНЫЕ ИДЕИ ДИСПЕРСИОННОГО АНАЛИЗА
Основной целью настоящего раздела является изложение идей одного из известнейших направлений математической статистики – дисперсионного анализа. Однако нам хотелось бы, чтобы читатель-социолог воспринял эти идеи не механически, а в свете понимания того, насколько он сможет использовать их для решения одной из самых главных задач любого научного исследования – изучения причинно-следственных отношений. Ведь дисперсионный анализ, по большому счету, предназначен именно для этого. И для того, чтобы его грамотно использовать, необходимо хотя бы кратко оговорить, в чем специфика того «понимания» этих отношений (в частности, понимания термина «причина»), которая заложена в соответствующем формализме. Этому, в частности, может способствовать также сравнение дисперсионного анализа с другими математико-статистическими методами изучения связи между переменными, с другими (не обязательно математико-статистическими) способами анализа каузальных отношений. Поэтому прежде, чем перейти непосредственно к описанию основ дисперсионного анализа, мы очень кратко рассмотрим некоторые методологические аспекты изучения причинных отношений вообще, с помощью математико-статистических методов – в частности; коснемся сути понятия эксперимента - того подхода к изучению причин, формализацией которого по существу является дисперсионный анализ, коротко коснемся специфики эксперимента именно в социологии. Кроме того, мы проанализируем, как прообразы идей, лежащих в основе дисперсионного анализа, «работают» при использовании простейшего коэффициента парной связи – корреляционного отношения, которое тоже можно рассматривать как способ изучения причинных отношений. Для более яркого преподнесения математико-статистического подхода мы коснемся также нестатистических методов изучения каузальных структур.
Т е м а 12
|
||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 . Воспользуемся рассуждениями из книги: Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976.
. Воспользуемся рассуждениями из книги: Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976.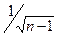 [60]. Так, если n = 200, то стандартное отклонение sr распределения выборочных коэффициентов корреляции будет равно примерно 0,071. Именно такое распределение изображено на рис. 11.1. слева. Нетрудно проверить также, что площадь под «хвостом»
[60]. Так, если n = 200, то стандартное отклонение sr распределения выборочных коэффициентов корреляции будет равно примерно 0,071. Именно такое распределение изображено на рис. 11.1. слева. Нетрудно проверить также, что площадь под «хвостом»
 . Если наша гипотеза верна, и, следовательно, распределение выборочных коэффициентов корреляции совпадает с левым распределением рисунка 11.1, сделать такую ошибку – ошибку первого рода – мы рискуем с вероятностью 0,05.
. Если наша гипотеза верна, и, следовательно, распределение выборочных коэффициентов корреляции совпадает с левым распределением рисунка 11.1, сделать такую ошибку – ошибку первого рода – мы рискуем с вероятностью 0,05.




