
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общее представление о социологических шкалах.Содержание книги
Поиск на нашем сайте
1. Общие принципы понимания измерения в социологии
Как мы уже отмечали во Введении, социолог не может отвлечься от проблемы измерения используемых им признаков. Напомним основные принципы теории измерений. Используемые ниже сокращения: ЭС – эмпирическая система, МС – математическая система, ЧС – числовая система. ЭС – это совокупность изучаемых объектов (например, в качестве таковой может служить множество студентов ГУ-ВШЭ), рассматриваемых как носители интересующих исследователя свойств (например, студенты могут интересовать исследователя как носители определенных политических взглядов). МС – это совокупность математических объектов, в которую ЭС отображается при измерении (в частности, ЭС может отображаться в ЧС). Итак, измерение – это отображение ЭС в МС:
И отображение это должно быть таким, чтобы у нас была гарантия адекватности «перехода» интересующих нас отношений между эмпирическими объектами в соответствующие им математические отношения между объектами МС. Так, если студенты интересуют исследователя лишь с точки зрения того, в какой степени каждый из них склонен к демократии, а рассматриваемая МС – числовая, то от чисел требуется, чтобы студенту с большей склонностью отвечало бы большее число. Чаще всего в качестве МС выступает ЧС. Тогда алгоритм, отображающий ЭС в МС, называется шкалой, соответствующий процесс измерения – шкалированием, а совокупность чисел, в которую мы отобразили элементы ЭС – шкальными значениями. Отметим, что нередко в социологии используются и нечисловые МС (например, граф, использующийся при изучении малой группы). Подчеркнем, что и ЭС, и МС – модели. Элементы ЭС – это не полноценные люди, а определенные «срезы» с них. Скажем, если студенты интересуют социолога как носители политических взглядов, то социологу должно быть безразлично, каков у них цвет волос (но только не в том случае, если вдруг окажется что блондины, скажем, более склонны к демократии, чем брюнеты). Элементы ЧС – не полноценные числа, а тоже лишь некоторые «срезы» с тех чисел, к которым мы привыкли в школе. Например, если в описанной выше ситуации с изучением политических взглядов студентов нас интересует только то, о чем шла речь, т.е. только сравнение студентов друг с другом по степени их склонности к демократии, то для нас будет осмыслен порядок получающихся чисел, но, скажем, соотношение 5-4=3-2 в таком случае не будет иметь смысла. 2.2. Определение номинальной, порядковой, интервальной шкалы
Из-за того, что при шкалировании используются не все обычные свойства чисел, рассматриваемых в качестве шкальных значений, совокупность таких значений оказывается определенной не однозначно. Так, если мы отображаем лишь степень склонности студентов к демократии, то соответствующая эмпирическая упорядоченность с одинаковым успехом отобразится и в числах 2, 18, 19, и в числах 128, 154, 2037. То преобразование, с точностью до которого определена совокупность шкальных значений каких-либо элементов рассматриваемой ЭС, называется допустимым преобразованием шкалы. Тип шкалы определяется тем, какая совокупность допустимых преобразований этой шкале отвечает. Содержание таблицы 2 позволяет понять, каким образом определяются наиболее распространенные в социологии типы шкал - номинальная, порядковая, интервальная).
Таблица 2. Определение основных типов шкал Одна шкала называется шкалой более высокого типа, чем другая, если совокупность допустимых преобразований первой шкалы включается в совокупность допустимых преобразований второй. Среди шкал, из таблицы 2 наиболее высокий тип имеет интервальная шкала, наиболее низкий – номинальная. Результаты измерения по шкале более высокого типа больше похожи на числа. Определение типа шкалы нужно нам не для «красоты». То, по какой шкале получены исходные данные, определяет, каким образом эти данные можно анализировать для получения нового знания. Интуитивно ясно, что далеко не все операции осмыслены для шкал любого типа. Скажем, если мы используем номинальную шкалу для измерения национальности и приписываем первому респонденту, русскому, 1, второму – татарину – 2, третьему, украинцу – 3, четвертому, чукче, - 4, то вряд ли будем считать имеющим смысл выражение: Как же определить, чтó именно мы имеем право делать с числами, полученными по той или иной шкале? В некоторых книгах ответ на этот вопрос дается путем перечня ряда методов, отвечающих определенным шкалам: для интервальной шкалы мы имеем право считать среднее арифметическое, моду и медиану; для порядковой – моду и медиану; для номинальной – только моду и т.д. Но такой подход вряд ли может считаться удовлетворительным. Во-первых, для всех методов перечня не составишь. И даже если это удастся сделать сегодня, то что делать с теми методами, которые будут изобретены завтра? Во-вторых, совершенно не ясно, что означает «разрешение» использовать метод. Ну, скажем, то, что среднее арифметическое нельзя использовать так, как мы это сделали в приведенном выше примере, ясно уже на уровне здравого смысла. А почему его нельзя использовать для порядковых шкал? А как определить, можно или нельзя использовать для номинальных шкал, скажем, регрессионный анализ? Ответ уже не столь очевиден. В-третьих, приведенный выше перечень, вообще говоря, неверен. Так, бывают случаи, когда среднее арифметическое можно использовать и для номинальных данных. Пусть, скажем, мы измерили пол: мужчинам приписали 1, а женщинам - 0. Для 10 человек получили последовательность: 0, 0, 1, 0, 1, 0, 0, 1, 1, 0. Нетрудно видеть, что соответствующее среднее арифметическое будет равно 0,4. Если мы будем интерпретировать это обстоятельство так, как это обычно делается (наиболее типичный представитель рассматриваемой совокупности людей имеет пол 0,4), но, конечно, получим ерунду. Но попытаемся дать другую интерпретацию: доля единичных значений нашего признака в изучаемой совокупности составляет 40%. Вряд ли кто-нибудь будет возражать против того, что такая интерпретация вполне допустима. Так почему бы не считать среднее арифметическое для пола? Интерпретировать надо адекватно, и все будет в порядке. Для решения поставленных вопросов в теории измерений был разработан специальный подход. 2.3. Проблема адекватности математического метода.
Интуитивно ясно, что, чем выше тип шкалы, тем более широкий круг методов применим для анализа соответствующих шкальных значений. Так, совершенно ясно, что к числам, полученным по номинальной шкале, многие традиционные математико-статистические методы не применимы. Это легко понять, рассмотрев две возможные номинальные шкалы из третьего столбца таблицы 2. Ясно, что, вообще говоря, очень многие методы будут давать разные результаты в зависимости от того, проанализируем ли мы с помощью выбранного метода числа (5, 5, 10, 185, 15) или же числа (25, 25, 3, 30, 1). Сравним, к примеру, средние арифметические значения первых трех объектов и последних двух объектов для каждой из номинальных шкал, приведенных в третьем столбце таблицы 2.
Делаем содержательный вывод: первое среднее меньше второго. Проделаем то же для второй шкалы.
Делаем противоположный вывод: первое среднее больше второго. А ведь если мы используем номинальную шкалу, то два рассмотренных набора шкальных значений содержат абсолютно одинаковую информацию! Значит, и результаты нашего анализа этих наборов должны быть одинаковыми. Естественно, у нас могут зародиться сомнения в целесообразности использования среднего арифметического для сравнения средних уровней двух рассматриваемых групп объектов. Существуют ли методы, результаты применения которых не зависят от того, какую из двух рассмотренных шкал мы выберем? Конечно. Этому условию будут удовлетворять все методы, опирающиеся на подсчет частот. Скажем, модальным значением в первом случае будет то, которым обладают первый и второй объект (скажем, если цифрой 5 закодирована национальность «татарин», то в рассматриваемом случае татар у нас – больше всего). То же – и во втором случае (снова «татар» у нас больше всего). Выводы не изменились. И вроде бы нет причин считать моду неподходящей статистикой для номинальной шкалы. Напротив, для интервальной шкалы большинство методов применимо. Попробуем, например, решить ту же задачу по сравнению средних для первых трех объектов и последних двух объектов для каждой из интервальных шкал, приведенных в третьем столбце таблицы 2. Для первой шкалы имеет место:
Другими словами, наш содержательный вывод состоит в том, что первое среднее меньше второго. Теперь попробуем проделать то же для второй интервальной шкалы из третьего столбца таблицы.
Вывод – тот же. Рассмотренный пример не дает оснований для возникновения сомнений в допустимости сравнения средних арифметических для интервальной шкалы. Разумно полагать, что аналогичные соображения будут справедливы и насчет моды. Более того, интуитивно ясно, методы, подходящие для номинальной шкалы, будут подходить и для интервальной. Все сказанное не случайно. Попытаемся выразить те же соображения в более строгом виде Математический метод называется формально адекватным, если результаты его применения не зависят от применения к исходным данным допустимых преобразований тех шкал, по которым эти данные получены. Если использовать это определение, то становится ясным, почему нельзя использовать среднее арифметическое для национальностей. Мы показали, что сравнение двух средних арифметических формально не адекватно относительно номинальных шкал. Покажем теперь, почему с формальной точки зрения нельзя рассчитывать средние для номинальной шкалы. Вернемся к обсужденному выше примеру. Напомним, что полученный содержательный вывод звучал так: «среднее между русским и украинцем равно татарину». Смысл этого утверждения изменится, если мы применим к набору исходных шкальных значений, скажем, следующее допустимое (для номинальной шкалы) преобразование: русским будем ставить в соответствие число 12, татарам – 5, украинцам – 10, чукчам – 11. Тогда среднее между русским и украинцем будет равно Напротив, наш результат, полученный с помощью расчета среднего арифметического для дихотомической шкалы, использованной нами при измерении пола, останется неизменным, если мы будем правильно его формулировать. А формулировку возьмем такую: среднее арифметическое делит интервал между числом, соответствующим женщине, и числом, соответствующим мужчине, в отношении 4:6 (что имело место выше и что по существу и говорило о доле единичных значений, равной 0,4). Покажем неизменность этого отношения на примере. Перекодируем произвольным образом значения пола: мужчинам припишем значение 48, а женщинам – 40. Нетрудно проверить, что тогда совокупность наших десяти шкальных значений превратиться в 40, 40, 48, 40, 48, 40, 40, 48, 48, 40, а среднее арифметическое будет равно 43,2, и будет верно соотношение: Поясним, почему выше мы дали определение не просто адекватности метода, а формальной адекватности. Дело в том, что формальная адекватность того или иного метода еще не делает его подходящим для решения социологической задачи соответствующего плана. Требуется еще другая адекватность, которую можно назвать содержательной – соответствие заложенной в методе модели сути решаемой задачи, априорным гипотезам исследователя (так, при осуществлении классификации объектов задействованная в алгоритме функция расстояния может быть формально адекватна типу используемых шкал, но содержательно совершенно не отвечать представлениям исследователя о похожести классифицируемых объектов).
Примеры задач. 1. Показать, что соотношение
является инвариантным относительно допустимых преобразований интервальных шкал и не является таковым относительно допустимых преобразования порядковых шкал. На основе соответствующих рассуждений объяснить, почему нельзя усреднять результаты ранжировок респондентами каких-либо объектов с целью получения оценочных шкал (оценочная шкала – это процесс приписывания рассматриваемым объектам чисел, отражающих усредненное отношение к этим объектам всей совокупности респондентов). Рекомендация. Допустимые преобразования используемой шкалы должны быть одними и теми же для рассматриваемых шкальных значений. В данном случае – и тех, для которых рассчитывается
2. Доказать, что значение коэффициента корреляции не изменится, если к исходным данным применить допустимое преобразование интервальных шкал.
3. Предположим, что мы имеем совокупность значений номинального признака Х с двумя значениями 0 и 1. Пусть p – доля “1”, q – доля “0”. Выразить
4. Описать, какова разница интерпретаций чисел 2, 3, 7 в ситуациях, когда эти числа получены по номинальной, порядковой или интервальной шкале.
5. Доказать формальную адекватность моды (в любом контексте ее использования) для номинальной шкалы
6. Доказать формальную адекватность рангового коэффициента корреляции (Спирмена или Кендалла) для порядковой шкалы.
Добавочная литература к теме 2 Обязательная Толстова Ю.Н. Измерение в социологии. М.: Инфра-М, 1998
ТЕМА 3 Стандартизация значений случайных величин. Виды некоторых специфических распределений [22], использующихся при переносе результатов с выборки на генеральную совокупность 3.1. Стандартизация (нормировка) значений случайной величины: способы и цели
В эмпирических исследованиях зачастую бывают задействованы такие признаки, значения которых не сравнимы друг с другом по величине. И если мы не обратим на это внимания, то при анализе данных можем придти к нелепости. Например, предположим, что мы хотим построить типологию какой-то совокупности людей, описываемых, в частности, значениями их зарплаты и возраста. Включаем компьютер, «просим» его осуществить классификацию наших респондентов. Компьютер умеет работать с числами. В соответствии с большинством известных алгоритмов классификации, оценивая по определенным правилам степень близости между всевозможными парами объектов, программа будет близкие объекты относить к одному классу, далекие – к разным. Представим себе две пары людей: респонденты первой пары отличаются друг от друга только тем, что у одного – зарплата на 50 рублей больше, чем у другого; объекты же второй пары – только тем, что у них такая же разница в возрасте (50 лет). Вероятно, при любом разумном алгоритме, если уж первые два респондента окажутся включенными в один класс, то и вторые – тоже, и обратно. Вряд ли это можно считать разумным: какова бы ни была решающаяся задача, различие зарплаты в 50 рублей вряд ли стоит принимать во внимание, а различие в возрасте в 50 лет – напротив, по-видимому, надо будет учесть. Могут возникнуть недоразумения и из-за того, что наблюдаемые значения рассматриваемых признаков будут «колебаться» вокруг сильно отличающихся друг от друга точек числовой прямой (если, например, среднее арифметическое значение одного признака равно 5000 (рублей), а другого – 50 (лет)). Чтобы подобных недоразумений не происходило, признаки обычно определенным образом нормируют (хотя, вообще говоря, бывают задачи, когда этого делать не надо). Нормировка бывает разной. Чаще всего делают так, чтобы среднее значение признака стало равным нулю, а остальные значения измерялись в «сигмах». Нетрудно видеть, что к такой ситуации приводит следующая нормировка (стандартизация) всех значений признака x: х Þ
3.2. Нормальное распределение (повторение). Если некоторая случайная величина x имеет нормальное распределение, то будем использовать для обозначения этого обстоятельства выражение: x ~ N (m, s). Напомним, что нормальное распределение задается двумя параметрами: m - математическое ожидание, s - стандартное (среднеквадратическое), отклонение (s2 – дисперсия). Р (х) = Из курса теории вероятностей читатель должен помнить, что кривая плотности нормального распределения представляет собой симметричный «холм», вершина которого находится над точкой X=m; ширина же «холма» зависит от величины s: чем больше эта величина, тем более пологим этот «холм» является.
Рис. 3.1. Функции плотности нормального распределения с с математическим ожиданием m = 2 и различными средними квадратическими отклонениями (s = 1 для F1(x); s = 2 для F2(x); s = 3 для F3(x))
Произвольная нормально распределенная случайная величина превращается в стандартизованную xстанд ~ N (0,1), если осуществить преобразование х Þ (мы получили тем самым стандартизованное распределение). О роли такого представления нормально распределенной случайной величины вы слышали в курсе теории вероятностей. Для хорошего восприятия дальнейшего материала важно вспомнить, что для нормального распределения хорошо изучено, какова вероятность попадания значения соответствующей случайной величины в разные отрезки числовой оси (подробнее о том, что из курса теории вероятности следует повторить, см. в конце настоящей лекции)
3.3. Распределение Хи-квадрат Пусть случайные величины x1, x2,..., xn - независимы и каждая имеет стандартное нормальное распределение N (0,1). Говорят, что случайная величина c n 2, определенная как
cn2 = x12 + x22,..., xn2
имеет распределение хи-квадрат с n степенями свободы [23]. Для этой случайной величины составлены разнообразные таблицы. Чаще всего они содержат значения р-квантилей. Заметим, что плотность распределения этой функции можно выразить определенной формулой (как мы выражали, например, плотность функции нормального распределения). Но эта формула очень сложна, поэтому мы не выписываем ее в основной части текста[24]. .
Подчеркнем, что существует не одно распределение хи-квадрат, а целое семейство таких распределений, каждый член семейства задан отвечающим ему значением n. Другими словами, для каждого n существует свое распределение хи-квадрат. И если нам понадобится таблица, задающая это распределение, то мы должны будем выбрать нужную из целого семейства таблиц, каждая из которых задается своим числом степеней свободы. Далее мы увидим, что понятие числа степеней свободы имеет смысл и для других распределений. Часто число степеней свободы рассматриваемого распределения обозначают сочетанием букв df (degree of freedom). Известно, что Мcn2 = n, Dcn2 = 2n, Mo cn2 = n – 2 (для n ³ 2). Для сравнения напомним, что нормальное распределение тоже задается парой двух параметров – математическим ожиданием и дисперсией; однако чтобы связать какое-либо значение нормально распределенной случайной величины x ~ N (m, s) с соответствующей вероятностью, нет необходимости выбирать нужную нам таблицу из некоторого семейства, поскольку в справочниках обычно фигурирует лишь одна таблица – для стандартизованной случайной величины xстанд ~ N (0,1); все необходимые сведения для случайной величины с произвольным распределением N (m, s) из нее могут быть получены. Приведем графики плотности распределения c22 и c32 (см. рис. 3.2).
Рис. 3.2. Функции плотности распределения «Хи-квадрат» с числом степеней свободы 2 и 3.[25] (вдоль вертикальной оси, строго говоря, следовало бы написать «плотность вероятности», а не «относительная частота»; второе, вообще говоря, годится лишь при работе с выборкой)!!!!!!!!!!!!!!!!!!!!!
Приведем примеры «Хи-квадрат»-распределений с другими числами степеней свободы, указывая при этом, вероятности попадания значений рассматриваемых случайных величин в некоторые полуинтервалы.
Рис. 3.3. Функция плотности распределения «Хи-квадрат» с числом степеней свободы 1. [26] (вдоль вертикальной оси, строго говоря, следовало бы написать «плотность вероятности», а не «относительная частота»; второе, вообще говоря, годится лишь при работе с выборкой)!!!!!!!!!!!!!!!!!!!!!!!!!
Рис. 3.4. Функции плотности распределения «Хи-квадрат» с числом степеней свободы 6 и 10.[27] (вдоль вертикальной оси, строго говоря, следовало бы написать «плотность вероятности», а не «относительная частота»; второе, вообще говоря, годится лишь при работе с выборкой)!!!!!!!!!!!!!!!!!!!!!
3.4.Распределение Стьюдента [28] (t-распределение) Пусть случайные величины x0, x1,..., x n – независимы и каждая имеет стандартное нормальное распределение N (0,1)[29]. Говорят, что случайная величина tn, определенная как
имеет распределение Стьюдента с n степенями свободы. M t n = 0; D t n = n / (n – 2) (n > 2); Mo = 0. При больших n вместо распределения Стьюдента обычно рекомендуется использовать стандартное нормальное распределение. Встает вопрос о том, какие выборки называть большими. В западной традиции большой называют выборку, если n ³ 30 (см., например, учебник Блумана). Отечественная наука более осторожна: большой называется выборка, если n ³ 100. Строгих правил здесь не может существовать в принципе. Все зависит от того, какая степень надежности получаемых выводов нам требуется. Ответ на вопрос об объеме выборки может дать только практика. При этом российские ученые опираются на практику использования математической статистики в естественных науках и технике, а западные учитывают и опыт гуманитарных наук, где погоня за большой точностью и надежностью зачастую теряет смысл, поскольку достаточно «грубыми» являются результаты измерений рассматриваемых признаков (социолога обычно волнует вопрос о том, то ли он меряет, что хочет, и вопрос о точности уходит на второй план). Так что мы далее будем считать, что выборки объема более 30 – достаточно большие для того, чтобы распределение Стьюдента подменять нормальным.
Рис. 3.5. Функции плотности распределения Стьюдента с различным числом степеней свободы. Для сравнение на том же графике приведена функция плотности нормального распределения. [30] КРАСНОЕ – МЕЛКИМ ШРИФТОМ И еще один вопрос должен был бы возникнуть у читателя (правда, за 10 лет чтения автором лекций по рассматриваемому предмету студентам-социологам нашелся лишь один слушатель, задавший этот вопрос): что делать, если n=1 или n=2? Дисперсия будет отрицательной? Нам представляется полезным дать ответ на этот вопрос, поскольку этот ответ позволит читателю-социологу вспомнить кое-что из интегрального исчисления и лишний раз убедиться в том, что полученные им на первом курсе вуза знания по высшей математике отнюдь не бесполезны. Ответ на указанный вопрос таков: при n=1 или n=2 дисперсия соответствующего распределения Стьюдента не существует. ДАЛЕЕ, до п. 3.5, - МЕЛКИМ ШРИФТОМ. Позволим себе привести здесь доказательство этого факта для n=1 (что, на наш взгляд, должно иметь определенное «воспитательное» значение). Плотность распределения Стьюдента имеет вид: (-¥ < х < +¥, напомним, что т.н. гамма-функция имеет вид: Г(z) =
где const – это некоторая величина, не зависящая от нашей переменной x.
Напомним, что: (1) дисперсия случайной величины х равна D(x) = M (x - M(x))2, (2) математическое ожидание случайной величины x с плотностью распределения f(x) вычисляется по формуле: M (x) = D(x) = M (x2) = Другими словами, интеграл расходится, т.е. интересующая нас дисперсия не существует
3.5. Распределение Фишера [31] (F – распределение, распределение дисперсионного отношения).
Пусть случайные величины h1, h2,...,h m; x1, x2,..., x n (m и n – натуральные числа) – независимы и каждая имеет стандартное нормальное распределение N (0,1). Говорят, что случайная величина F m , n, определенная как Fm , n = имеет F-распределение с параметрами m и n. Натуральные числа m и n называют числами степеней свободы. М F m, n = n / (n – 2) для n > 2, D F m, n = (2 n2(m + n – 2)) / (m (n – 2) 2(n –4)) для n >4 ; Mo = n (m– 2) / m (n + 2), m > 1.
Рис. 3.6. Функции плотности F-распределения с разным числом степеней свободы[32] Повторение отдельных фрагментов курса по теории вероятностей
1. Общее представление о вероятностных таблицах. Принципы их использования. 2. Определение нормального распределения. Вид нормальной кривой, «физический» смысл отвечающих ей математического ожидания и дисперсии. Целесообразность измерения значения случайной величины в единицах s (среднего квадратического отклонения). Соотношение площадей под нормальной кривой и вероятностей попадания в отрезки (m ± s, m ± 2s, m ± 3s). Определение размера отрезка (в единицах сигма) при заданной доле попадания в него. Функция Лапласа. Следует запомнить, каковы доли площадей под разными частями нормальной кривой; учесть, что целому числу s обычно отвечают «корявые» проценты: одна s – 68,3 % площади, 2 s – 95,4%; а «круглые» процентам отвечает «корявое» число «сигм»: 90% - 1,64 s, 95% - 1,96 s, 99% - 2, 57s и т.д. Эти и другие значения представлены на рис. 3.7. Необходимо также понимать связь функции плотности распределения с функцией распределения и принципы нахождения квантилей распредлеления (например, процентилей). Этому также может способствовать рис. 3.7, на котором отражено, как из функции плотности получается функция распределения (отвечающая накопленным процентам) и как по функции распределения можно рассчитывать процентили.
Рис. 3.7. Доли площадей под разными частями кривой плотности нормального распределения. Указание процентилей [33] (подобные иллюстрации можно найти и в других работах[34]). 3. Правило трех сигм. 4. Роль стандартизации нормально распределенных случайных величин при использовании соответствующих вероятностных таблиц. Использование таблицы для стандартизованной величины при получении характеристик распределения произвольной нормально распределенной случайной величины. Пример того, как по величине отрезка под стандартизованной нормальной кривой можно определять вероятность попадания в этот отрезок соответствующей случайной величины, можно найти на рис. 3.8.
Рис. 3.8. Иллюстрация того, как отрезок диапазона изменения стандартизованной нормальной кривой связан с отвечающей этому отрезку площадью под этой кривой (т.е. с вероятностью попадания значения величины в рассматриваемый отрезок).[35]
- таблицы значений функции Лапласа Ф(х)[36]; - таблицы, в которой задана вероятность попадания в правый конец графика функции плотности (по заданному z определяется вероятность того, что f(x) > z)[37]; - таблицы значений удвоенной функции Лапласа[38]; - таблицы верхних процентных точек стандартного нормального распределения[39]. 6. Таблицы, составленные для всех остальных рассмотренных выше распределений. Их разные виды. Квантили распределений. Понимание того, что таблицы, как правило, содержат значения р -квантилей. Принцип практической невозможности маловероятных событий
Примеры задач
1. Доказать, что среднее арифметическое значение стандартизованного признака равно нулю, а среднее квадратическое отклонение – единице. 2. Известно, что распределение оценок, полученных абитуриентами при ответе на некоторый 20-балльный тест, имеет вид N (10, 3). Какова вероятность того, что абитуриент получит балл от 7 до 11? Объяснить, как находится подобная вероятность при использовании четырех видов вероятностных таблиц. 3. С какой площадью под графиком функции плотности стандартизованного нормального распределения соотносится значение функции Лапласа? 4. Как следует понимать упомянутое выше выражение «верхние процентные точки» из книги Тюрина и Макарова? В некоторых работах эти точки называются процентилями. Что такое процентиль? Что такое квантиль (частным случаем которого является процентиль)? Какие еще виды квантилей вы знаете? ТЕМА 4 Предельные теоремы. [40] При изучении результатов наблюдений над реальными массовыми случайными явлениями (над выборочными значениями изучаемых случайных величин) часто наблюдаются определенные закономерности, обладающие свойством устойчивости при рассмотрении разных выборок. Суть устойчивости состоит в том, что конкретные свойства каждого явления почти не сказываются на среднем результате. Наблюдаемые на выборке характеристики случайных величин при неограниченном увеличении количества и объема выборок становятся практически не случайными. Предельные теоремы, о которых идет речь ниже, фактически устанавливают зависимость между случайностью и необходимостью. По смыслу эти теоремы можно разбить на две большие группы – центральную предельную теорему и закон больших чисел (хотя по сути они отражают одно и то же).
4.1. Центральная предельная теорема Центральной предельной теоремой обычно называют группу утверждений (точнее, каждое утверждение из этой группы), которые устанавливают связь между законом распределения суммы случайных величин и его предельной формой - нормальным законом распределения. Различные формулировки отличаются условиями, которые накладываются на исходные случайные величины. Прежде всего напомним формулировку (в упрощенном виде[41]) одной из известных теорем А.М.Ляпунова (1857–1918) (впервые, но в более простом виде, эта теорема была доказана П.Л. Чебышевым (1821–1894) в 1887 году). Теорема Ляпунова (1901). Распределение суммы независимых случайных величин Х1, Х2, Х 3,..., Хn приближается к нормальному закону распределения при неограниченном увеличении n, если выполняются следующие условия: 1) все величины имеют конечные математические ожидания и дисперсии; 2) ни одна из величин по своему значению резко не отличается от всех остальных, т.е. оказывает ничтожное влияние на их сумму. Таким образом, предельное распределение суммы случайных величин в условиях рассмотренной теоремы не зависит от вида распределений самих случайных величин. На опыте установлено, что распределение суммы независимых случайных величин, у которых дисперсии не отличаются резко друг от друга, довольно быстро приближаются к нормальному. Уже при числе слагаемых, большем 10, распределение суммы можно заменить нормальным. Теорема Ляпунова справедлива и для дискретных случайных величин. Отметим, что центральная предельная теорема имеем большое значение для социолога, поскольку она объясняет причину большого распространения в природе (в том числе – в обществе) нормального распределения, оправдывает делаемые зачастую априори, без проверки, предположения о нормальности тех распределений, которые анализируются в социологических исследованиях. Приведем пример. В ряде методов шкалирования предполагается, что мнение человека о любом объекте плюралистично. Это означает, что если бы у нас имелся инструмент измерения такого мнения, и мы имели бы возможность использовать его много раз, то, вообще говоря, каждый раз получали бы разные значения. Этим значениям отвечало бы некоторое распределение вероятностей. Важное для нас утверждение состоит в том, что при этом обычно полагают, что указанное распределение нормально (это делается, например, в методе парных сравнений – одном из известных способов получения экспертных оценок[42]). И такую посылку вполне можно принять, если опереться на центральную предельную теорему.
Другая формулировка теоремы Ляпунова. Если случайная величина Х имеет математическое ожидание МХ и дисперсию DX, то распределение среднего арифметического
(в таких случаях говорят, что Или, в других обозначениях, то же самое может быть записано следующим образом:
| ||||||||||||||||||
|
| Поделиться: |

 ЭС МС.
ЭС МС. (среднее арифметическое между русским и украинцем равно татарину).
(среднее арифметическое между русским и украинцем равно татарину). .
.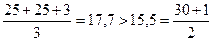

 , т.е. чукче (а не татарину, как выше). Говоря формально, содержательный результат изменился в результате допустимого преобразования исходных (номинальных) шкал. Метод (подсчет среднего арифметического) формально не адекватен.
, т.е. чукче (а не татарину, как выше). Говоря формально, содержательный результат изменился в результате допустимого преобразования исходных (номинальных) шкал. Метод (подсчет среднего арифметического) формально не адекватен. . Отношение, говорящее о доле значений «48», осталось тем же.
. Отношение, говорящее о доле значений «48», осталось тем же.
 , и тех для которых считается
, и тех для которых считается  .
. и Sx через p и q.
и Sx через p и q.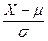



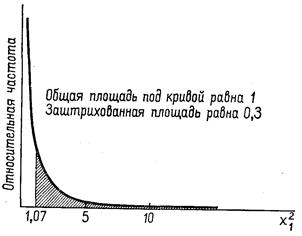




 ). При n=1 f (x) принимает вид:
). При n=1 f (x) принимает вид:

 , (3) математическое ожидание величины, распределенной по закону Стьюдента, равно нулю. Поэтому для рассматриваемого нами случая имеет место цепочка равенств:
, (3) математическое ожидание величины, распределенной по закону Стьюдента, равно нулю. Поэтому для рассматриваемого нами случая имеет место цепочка равенств: = const
= const  = (x – arctg x) |+µ-µ = -µ - µ = -µ
= (x – arctg x) |+µ-µ = -µ - µ = -µ ,
,
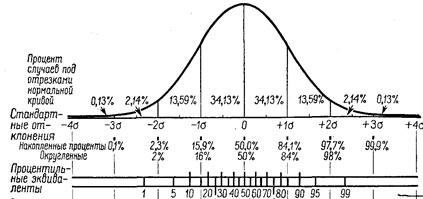

 приближается к нормальному с математическим ожиданием МХ и дисперсией DX / n. Другими словами,
приближается к нормальному с математическим ожиданием МХ и дисперсией DX / n. Другими словами, )
)


