
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еще раз о задачах математической статистики. Точечное оценивание параметровСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
5.1. О задачах математической статистики Главными задачами математической статистики, как мы уже отмечали, являются (а) изучение случайных величин путем осуществления выборочных оценок параметров их распределений и (б) перенос результатов с выборки на генеральную совокупность. Известны два подхода, позволяющие осуществлять упомянутый перенос: статистическое оценивание параметров и проверка статистических гипотез. Прежде, чем перейти к их описанию, напомним, что сам термин «параметр распределения» имеет смысл лишь для генеральной совокупности. В выборке каждому параметру отвечает некоторая специальным образом подобранная статистика, т.е. функция от наблюдаемых, выборочных, значений рассматриваемой случайной величины (напомним, что для выборки «случайная величина» превращается в «признак»). Удачность подбора статистики, отвечающей какому-либо параметру, по существу и означает то, что с помощью этой статистики можно судить о том, каков генеральный параметр. Ниже мы проанализируем, какими качествами для этого должна обладать статистика, и покажем, каким образом соответствующие оценки можно находить. Существует два способа, два вида оценивания параметров: точечное и интервальное. Точечное оценивание состоит в том, что мы вычисляем выборочное значение статистики, отвечающей нашему параметру, и именно это значение считаем хорошей выборочной оценкой генерального значения параметра. Интервальное оценивание происходит по иной схеме. Если t -генеральное значение параметра, а t – выборочное значение соответствующей статистики, то интервальное оценивание означает указание того, что с некоторой вероятностью Р значение t будет заключено в интервале t - D £ t £ t + D (точнее: с вероятностью Р указанный интервал «накроет» значение параметра t). При этом предполагается, что величины Р и D очевидным образом детерминируют друг друга: чем больше одна, тем больше и другая (ясно, что исследователю всегда хочется, чтобы величина D была бы поменьше, а величина Р – побольше, однако одно желание противоречит другому). Правила построения и точечных, и интервальных оценок для большинства известных параметров вероятностных распределений даются математической статистикой. Заложены они и в большинстве известных пакетов прикладных программ для ЭВМ. Однако механическое использование вычислительной техники не может способствовать успешному решению социологических задач. Ряд величин, необходимых для осуществления оценки, исследователь должен задать сам (скажем, в рассмотренном выше соотношении между D и Р исследователь должен сам выбрать, что для него важнее). А от выбора зависит интерпретация оценки. Эта интерпретация опирается на своеобразное статистическое видение реальности. Поэтому для эффективного использования положений математической статистики в эмпирическом социологическом исследовании необходимо понимать принципы осуществления статистических оценок. Мы опишем их на примерах рассмотрения наиболее популярных параметров.
5.2. Точечные оценки параметров. Предъявляемые к ним требования
Разумность выбора выборочного среднего арифметического в качестве точечной оценки генерального математического ожидания подтверждается центральной предельной теоремой и законом больших чисел, о чем пойдет речь ниже. Роль этих утверждений станет ясной, если мы обратимся к рассмотрению смысла тех свойств, которыми, в соответствии с положениями математической статистики, должна обладать «хорошая» точечная оценка того или иного параметра. Однако пока отвлечемся от качества точечных оценок и опишем некоторые модельные представления, типичные для названной науки. Представим себе, что мы имеем некоторую генеральную совокупность и строим на ее основе бесконечное количество выборок одного и того же объема n, для каждой из которой вычисляем интересующую нас статистику – в данном случае среднее арифметическое значений нашей случайной величины. Схематически эту процедуру можно выразить следующим рисунком
Рис. 5.1. Схематическое изображение процесса организации бесконечного количества выборок (одного и того же объема n) и получения соответствующей совокупности выборочных средних арифметических
Другими словами, мы имеем бесконечное количество выборочных средних
Эти средние можно считать реализацией некоторой случайной величины. Распределение таких средних хорошо изучено. Оно является нормальным с параметрами (mx,
Опр. Величина
называется средней (стандартной) ошибкой среднего, или средней (стандартной) ошибкой выборки для признака Х. Таким образом, стандартная ошибка среднего – это стандартное (среднее квадратическое) отклонение выборочного распределения средних значений Х, отвечающих бесконечному числу разных мыслимых выборок объема n из изучаемой генеральной совокупности с дисперсией s2. Подчеркнём, что средняя ошибка выборки говорит о порядке величины случайного отклонения выборочной оценки среднего от "истинного" значения параметра генеральной совокупности (в данном случае «истинное» значение – это mx). Ясно, что упомянутая ошибка уменьшается с увеличением объёма выборки и с уменьшением среднего квадратического отклонения самого признака, т.е. с увеличением однородности совокупности по этому признаку (можно показать, что та же ошибка увеличивается с увеличением объёма генеральной совокупности; однако генеральную совокупность в большинстве интересующих социолога случаев имеет смысл считать бесконечной, а в таком случае очевидно, что об увеличении ее объема говорить нет смысла). Распределение, аналогичное описанному распределению выборочных средних, можно строить для значений любой статистики (т.е. для точечных оценок любого параметра заданного распределения). Далее мы этим будем активно пользоваться при обсуждении вопроса о том, что такое «хорошая» точечная оценка («хорошая» статистика). Все, что было сказано относительно математического ожидания и среднего арифметического, можно обобщить на любой параметр и отражающую его статистику. Рассмотрим некоторый параметр t (в качестве такового может выступать математическое ожидание, дисперсия, коэффициент корреляции и т.д.). Пусть имеется какая-то выборка, содержащая информацию о нашем параметре, и мы выбрали некую статистику t, значение которой для выборки служит точечной оценкой нашего параметра. Чтобы подобные точечные оценки были «хорошими», требуется, чтобы они удовлетворяли некоторым свойствам. Для понимания смысла этих свойств представим себе картину, аналогичную изображенной на рис. 3.1, т.е. представим, что мы осуществляем огромное количество выборок, для каждой из которых рассчитываем значение рассматриваемой статистики. Этим значениям отвечает некоторое распределение. Опр. Указанное распределение обычно называется выборочным распределением рассматриваемой статистики t ( точнее, следовало бы говорить о распределении оценок, получаемых с помощью выбранной статистики). Для большей ясности заметим, что распределение среднего арифметического (точнее, средних арифметических), представленное на рисунке 1, - частный случай такого выборочного распределения. Каждое выборочное распределение любой статистики t (оценивающей любой генеральный параметр t) имеет свои параметры – в частности, свое математическое ожидание и дисперсию (как выше это имело место для выборочного распределения среднего арифметического). Для многих параметров t подобные распределения изучены, определен соответствующий закон, найдены основные его характеристики. Ниже в соответствии со сложившейся в литературе традицией, термины статистика и оценка иногда будем использовать как синонимы (до сих пор оценками у нас служили конкретные выборочные значения статистики). А именно, введем следующее определение. Опр. Иногда будем называть оценкой параметра t самое статистику t (а не ее отдельное значение, как раньше). Соответственно, будем говорить о выборочном распределении оценки (вместо выборочного распределения статистики). Вместо t иногда будем использовать обозначение tn в знак того, что при вычислении значений t используются выборки объема n. Надеемся, что предлагаемое смешение понятий “оценка” и “статистика” не приведет к недоразумениям. Итак, рассмотрим свойства «хороших» точечных оценок (Гласс и Стэнли, 1976, с. 228-232; Калинина, Панкин,1998,с.162-174). Опр. Оценка t параметра t называется несмещенной, если среднее выборочного распределения оценки t (при любом фиксированном объеме выборок n) равно величине оцениваемого параметра: M t = t. Несмещенность статистики требуется для повышения вероятности того, что наше единственное выборочное значение этой статистики будет достаточно близко к генеральному значению соответствующего параметра. Для смещенных оценок повышается вероятность большой ошибки.
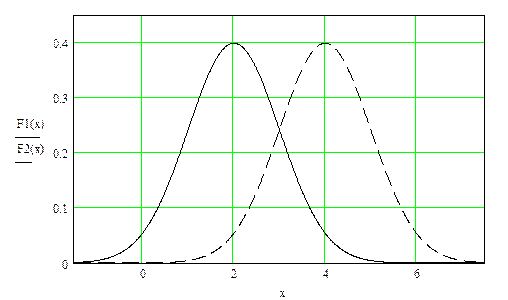
Mt t Рис. 5.2. Иллюстрация того, что смещенность оценки повышает вероятность того, что ее выборочное значение будет далеко отстоять от генерального (Mt - математическое ожидание выборочных оценок параметра t, полученных с помощью смещенной статистики t; t - генеральное значение параметра; неравенство Mt ¹ t означает смещенность статистики t; сплошной линией F1(x) обозначено распределение упомянутых выборочных оценок;пунктирной F2(x)– то распределение гипотетических оценок, которые были бы получены с помощью несмещенной статистики).
Для пояснения обратимся к рис. 5.2. Предположим, что для оценки некоторого параметра t используется значение нормально распределенной статистики t, распределение которой представлено на рисунке кривой F1 (x) (сплошная линия). В нашем распоряжении имеется только одно значение статистики t – то, которое мы вычислили для нашей единственной выборки. Очевидно, с относительно большой вероятностью это значение попадет в ближайшую окрестность точки x = 2 (поскольку Mt = 2). Вероятность же попасть в ближайшую окрестность точки x = 4 относительно мала. А ведь генеральное значение параметра t равно именно 4. Это и означает смещенность статистики t: Mt ¹t. Ясно, что у нас резко возросла бы вероятность попадания выборочной оценки параметра в окрестность точки x=4, если бы мы пользовались другой статистикой, расределение которой представлено на рис. 5.2 кривой F2 (x) (пунктирная линия).
Выборочное среднее является несмещенной оценкой генерального математического ожидания (точнее, следовало бы говорить, что среднее арифметическое дает несмещенные оценки, если полагать, что оценка – это конкретное значение статистики для выборки). Это следует из центральной предельной теоремы. Если исходная совокупность симметрична, то несмещенной оценкой того же математического ожидания является и выборочное значение медианы. Если совокупность будет не только симметричной, но и унимодальной, то несмещенной оценкой математического ожидания явится и мода[45]. Для несмещенных оценок имеют смысл следующие определения. Опр. Среднее квадратическое отклонение выборочного распределения статистики, отвечающей некоторому рассматриваемому параметру, будем называть средней ошибкой выборки для оцениваемого параметра. Таким образом, для каждого оцениваемого параметра существует своя средняя ошибка выборки. Если же говорят о средней ошибке выборки вообще, то имеют в виду среднюю ошибку выборки для математического ожидания.
Известно много представляющихся естественными, но смещенных оценок. Так, вообще говоря, смещенной является оценка генерального коэффициента корреляции r между двумя случайными величинами, когда в качестве оценивающей статистики фигурирует выборочный коэффициент корреляции r между соответствующими признаками, определяемый по знакомой нам формуле
r =
Несмещенной эта оценка является только в том случае, когда r = 0. Смещенной является и оценка генеральной дисперсии с помощью расчета известной формулы:
D2 = Именно для того, чтобы сделать эту оценку несмещенной, в знаменателе указанной формулы пишут не n, а (n – 1) (несмещенной такая оценка будет для любой исходной совокупности). Чтобы еще раз показать, зачем же нужно стремиться к тому, чтобы используемая статистика давала нам именно несмещенную оценку параметра, рассмотрим распределения только что упомянутых оценок дисперсии. Рассмотрим рис. 5. 3.
Рис. 5.3. Выборочные распределения величин Снова «частоту» надо заменить на «вероятность»!!!!!!!!!!!!!!!!!! И убрать точку около икса с чертой (s¢x)2 = для случайных выборок объема 6 из нормального распределения с дисперсией s2 = 100[46]
Среднее, отвечающее распределению величины sx2, равно 100, т.е. интересующему нас значению генерального параметра. Среднее, отвечающее величине (s¢x)2, смещено относительно значения генерального параметра: оно равно 83,3. Величина подобного смещения может быть измерена с помощью коэффициента
.В данном случае величина смещения довольно большая: она равна
Опр. Оценка параметра называется состоятельной, если при увеличении объема выборки ее значение приближается к значению генерального параметра, который она оценивает:
Нетрудно понять смысл требования состоятельности. Если оценка не является состоятельной, то у нас не будет гарантии того, что увеличение объема выборочной совокупности приближает нашу оценку к «генеральному» значению изучаемого параметра (должно быть справедливым положение: чем больше объем выборки, тем ближе наша выборочная оценка генерального параметра к его истинному значению). Среднее арифметическое – состоятельная оценка математического ожидания. И следует это из закона больших чисел (см. приведенную выше формулировку частного случая теоремы Чебышева).
Если несмещенность и состоятельность – понятия абсолютные (относительно каждой статистики в принципе можно сказать, смещена она или не смещена, состоятельна или нет), то эффективность – понятие относительное: можно говорить только о том, что одна статистика более эффективна, чем другая. Более эффективной обычно считается та статистика, которая имеет меньшую дисперсию своего выборочного распределения.
Для примера упомянем, что выборочные мода и медиана являются несмещенными и состоятельными оценками математического ожидания (более точно, для медианы несмещенность имеет место только в случае симметричности генерального распределения, а для моды – для симметричного и унимодального)[47]. Но они менее эффективны, чем среднее арифметическое. Так, дисперсия ошибки выборочной медианы (т.е. дисперсия выборочного распределения медианы) равна
Рис. 5.4. Выборочное распределение среднего (см. [Гласс и Стэнли, 1976, с. 232]) Md заменить на Mе!!!!!!!!!!! Убрать точку около икса с чертой
Смысл требования эффективности тоже представляется очевидным. Если одна оценка (статистика) менее эффективна, чем другая, то, взяв значение первой (вычисленное для нашей одной - единственной выборки), мы имеем больший шанс «промахнуться», получить значение, сильно отличающееся от значения соответствующего генерального параметра. Заметим, что, пользуясь вычисленной для выборки относительной частотой встречаемости того или иного интересующего нас события (скажем, тем, что в выборке мы имеем 40% женщин) мы фактически полагаем, что эта частота является хорошей точечной оценкой соответствующей генеральной вероятности (в нашем случае – полагаем, что эта вероятность близка к 0,4). О том, какова средняя ошибка выборки для доли (т.е. какова дисперсия выборочного распределения этой статистики) см. ниже.
ТЕМА 6
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 579; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.208.127 (0.009 с.) |

 В качестве статистики, отвечающей в вышеприведенном смысле математическому ожиданию, выступает среднее арифметическое. Другими словами, мы считаем, что, если Х1, Х2, Х 3,..., Х n - выборочные значения некоторой случайной величины x (n – объем выборки), то точечной оценкой математического ожидания Mx (mx) этой случайной величины мы считаем число
В качестве статистики, отвечающей в вышеприведенном смысле математическому ожиданию, выступает среднее арифметическое. Другими словами, мы считаем, что, если Х1, Х2, Х 3,..., Х n - выборочные значения некоторой случайной величины x (n – объем выборки), то точечной оценкой математического ожидания Mx (mx) этой случайной величины мы считаем число = (Х1 + Х 2+ Х 3 +... + Х n)/ n
= (Х1 + Х 2+ Х 3 +... + Х n)/ n

 5
5



 ). Это следует из рассмотренной в предыдущей лекции теоремы Ляпунова (второй ее формулировки).
). Это следует из рассмотренной в предыдущей лекции теоремы Ляпунова (второй ее формулировки). =
= 
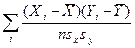


 и (s x )2 =
и (s x )2 = 
 , поскольку именно с помощью этого коэффициента (s¢x)2 выражается через sx2:
, поскольку именно с помощью этого коэффициента (s¢x)2 выражается через sx2: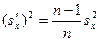
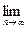 P (|tn - t| < e) = 1.
P (|tn - t| < e) = 1. 
 , т.е. примерно в 1,57 раз больше дисперсии среднего арифметического.
, т.е. примерно в 1,57 раз больше дисперсии среднего арифметического.



