
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследовать на непрерывность и построить график функции f(x). Найти скачок функции в точках разрыва.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Контрольные вопросы: 1. Что называется функцией? 2. Что называется пределом функции в точке? 3. Перечислите свойства пределов. 4. Какое необходимое условие существования предела функции вы знаете? 5. Что называется пределом функции на бесконечности? 6. Сформулируйте первый замечательный предел функции и следствия из него. 7. Сформулируйте второй замечательный предел функции и следствия из него. 8. Какая функция называется непрерывной? 9. Перечислите виды точек разрыва. 10. Дайте определения каждого вида точек разрыва.
ПРАКТИЧЕСКАЯ РАБОТА №2
«Правила дифференцирования. Производная сложной функции» Цель: сформировать навыки нахождения производных элементарных и сложных функций,применять основные правила дифференцирования.
Теоретическая часть Понятие производной является основным понятием дифференциального исчисления. Метод дифференциального исчисления был создан в 17 и 18вв. С возникновением этого метода связаны имена двух великих математиков—И. Ньютона и Г.В. Лейбница. Возникло дифференциальное исчисление при решений задач о мгновенной скорости движения материальной точки. Рассмотрим неравномерное движение материальной точки. Средняя скорость ее за промежуток времени Δt равна Эта и другие задачи приводят к понятию производной функции. Отношение
Определение. Производной функции y=f(x) в точке х называется предел отношения приращения функции ∆y к приращению аргумента ∆x, когда приращение аргумента стремится к нулю:
Функция может иметь производную в точке х0 только тогда, когда функция определена и непрерывна во всех точках некоторой окрестности х0 и говорим, что функция дифференцируема в этой точке. Правила дифференцирования. Пусть даны функции u, v и w. 1. Производная суммы (разности) равна сумме (разности) производных: (u+v-w)/ = u/+v/-w/ . 2. Производная произведения: (uv)/ =u/v+uv/. 3. Производная частного: 4. Постоянный множитель можно вынести за знак производной: (Cu)/=Cu/. 5. Производная постоянной равна нулю: C/=0,
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |

 2)
2)  3)
3) 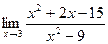 4)
4) 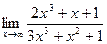 5)
5)  6)
6) 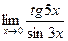 7)
7) 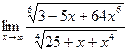 8)
8) 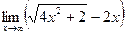 9)
9) 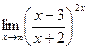 2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертеж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертеж.
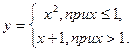
 2)
2)  .
2)
.
2)  .
3)
.
3)  4)
4) 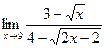 .
5)
.
5) 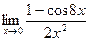 6)
6) 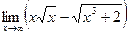 7)
7)  9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертеж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертеж.
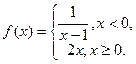
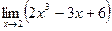 2)
2) 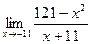 .
3)
.
3) 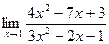 4)
4) 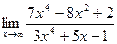 5)
5)  6)
6)  7)
7)  8)
8)  9)
9) 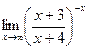 2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
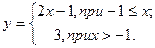
 2)
2) 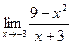 3)
3) 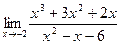 4)
4) 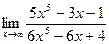 5)
5)  6)
6) 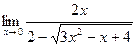 7)
7) 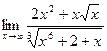 8)
8)  9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.

 .
2)
.
2)  3)
3) 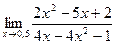 .
4)
.
4) 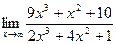 5)
5) 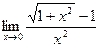 6)
6)  7)
7)  8)
8)  9)
9) 
 .
2)
.
2)  3)
3)  .
4)
.
4)  5)
5)  6)
6)  7)
7)  8)
8)  9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж. 
 .
2)
.
2)  3)
3) 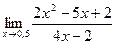 .
4)
.
4) 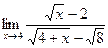 6)
6) 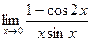 7)
7)  8)
8) 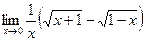 9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
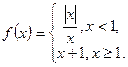
 (x2-7x+10).
2)
(x2-7x+10).
2)  3)
3) 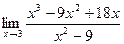 .
4)
.
4)  5)
5)  6)
6) 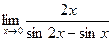 7)
7)  8)
9)
8)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.

 2)
2) 
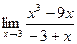 3)
3)  .
4)
.
4)  5)
5)  6)
6)  7)
7)  8)
8)  9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.

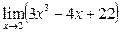 2)
2)  3)
3) 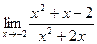 .
4)
.
4)  5)
5) 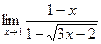 6)
6) 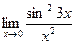 7)
7) 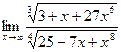 8)
8)  9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
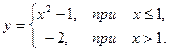
 3)
3) 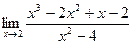 .
4)
.
4) 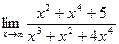 5)
5)  6)
6) 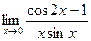 7)
7)  8)
8)  9)
9) 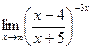 2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.

 (2x2-x+3).
2)
(2x2-x+3).
2)  3)
3)  .
4)
.
4) 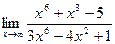 5)
5) 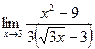 6)
6)  7)
7)  8)
8)  9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж

 .
2)
.
2) 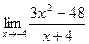 3)
3) 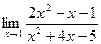 .
4)
.
4) 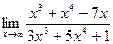 5)
5) 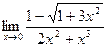 6)
6) 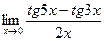 7)
7) 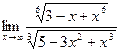 8)
8) 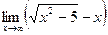 9)
9)  2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.

 3)
3) 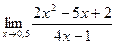 .
4)
.
4)  5)
5) 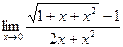 6)
6) 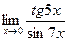 7)
7)  8)
8)  9)
9) 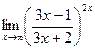 2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.
2. Для данной функции у требуется:
-найти точки разрыва, их тип;
-найти скачок функции (если есть);
-сделать чертёж.

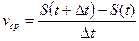 . Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть
. Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть 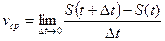 .
.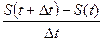 называется разностным отношением, а его предел
называется разностным отношением, а его предел 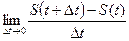 - производной функции S(t) и обозначается S/(t).
- производной функции S(t) и обозначается S/(t).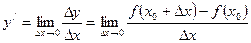 .
.



