
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точек перегиба и участков выпуклости и вогнутости функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1) Сначала находятся критические точки второго рода, т.е. точки, в которых вторая производная равна нулю или не существует. 2) Затем область определения функции разбивается на интервалы критическими точками и точками разрыва функции и определяется знак второй производной Порядок действий при этом рекомендуется следующий. 1. Найти область определения функции. 2. Найти 3. Определить критические точки второго рода и пронумеровать их в порядке возрастания. 4. Составить таблицу II.
Пример 6. Найти интервалы выпуклости, вогнутости и точки перегиба функции 1. ▲ Областью существования функции является весь бесконечный интервал 2. Найдем производные: 3. Вторая производная существует при всех Так как так как так как Вторая производная равна нулю 4. Составим таблицу II.
Замечание. Условимся в дальнейшем выпуклость вверх и выпуклость вниз графика в таблице обозначать так: Пример 7. Найти интервалы выпуклости, вогнутости и точки перегиба функции 1. ▲ Область определения функции 2. Найдем производные:
3. Вторая производная не существует 4. Составим таблицу II, знак второй производной
Пример 8. Найти интервалы выпуклости, вогнутости и точки перегиба функции 1. ▲ Область определения функции 2. Найдем производные: 3. Вторая производная 4. Составим таблицу II, знак второй производной
Пример 9. Найти интервалы выпуклости, вогнутости и точки перегиба функции 1. ▲ Область определения функции 2. Найдем производные:
3. Вторая производная АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Может оказаться, что размеры графика данной функции Определение. Прямая Различают три вида асимптот: вертикальные (параллельные оси Прямая
Для разыскания вертикальных асимптот кривой 1) находим на оси 2) выделяем те из них, в которых хотя бы один из пределов функции Наклонные асимптоты Теорема 4. Для того чтобы график функции
Аналогично для случая Горизонтальная асимптота (частный случай наклонной асимптоты Если Правило отыскания асимптот очевидно из следующего образца. Пример 10. Найти асимптоты кривой 1. ▲ Найдем область определения функции:
Функция не определена в точках
Следовательно, прямые 2. Найдем левую наклонную асимптоту:
Следовательно, имеем слева горизонтальную асимптоту Найдем правую наклонную асимптоту:
Значит, справа имеем горизонтальную асимптоту
Пример 11. Найти асимптоты кривой 1. ▲ Найдем область определения функции:
Аналогично получаем Прямая 2. Для нахождения левой наклонной асимптоты вычислим
Следовательно, прямая Аналогично для правой наклонной асимптоты получаем
Следовательно, прямая
Пример 12. Найти асимптоты кривой 1. ▲ Найдем область определения функции:
Значит, прямая 2. Найдем правую наклонную асимптоту (так как
Следовательно, наклонной асимптоты нет.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 в каждом из полученных интервалов (для чего достаточно определить знак
в каждом из полученных интервалов (для чего достаточно определить знак  , функция выпукла вниз, где
, функция выпукла вниз, где  , – выпукла вверх.
, – выпукла вверх. .
.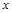

 на интервалах и поведение в к. т. II
на интервалах и поведение в к. т. II

 .
. .
. .
. . Критическая точка II рода
. Критическая точка II рода  . Разобьем область определения функции на интервалы
. Разобьем область определения функции на интервалы  и определим знак
и определим знак  в каждом из них. Для этого достаточно определить знак
в каждом из них. Для этого достаточно определить знак  .
. , то на интервале
, то на интервале  функция выпукла вверх;
функция выпукла вверх; , то на интервале
, то на интервале  функция выпукла вверх;
функция выпукла вверх; , то на интервале
, то на интервале  функция выпукла вниз.
функция выпукла вниз. . При переходе через точку
. При переходе через точку 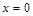 вторая производная не меняет знак, следовательно, в точке
вторая производная не меняет знак, следовательно, в точке  вторая производная меняет знак, следовательно, в точке
вторая производная меняет знак, следовательно, в точке 


 .
. .
. .
. ,
,
 .
. и равна нулю. Вторая производная равна нулю
и равна нулю. Вторая производная равна нулю  . Единственная критическая точка второго рода
. Единственная критическая точка второго рода  области определения не принадлежат. Разобьем область определения функции на интервалы
области определения не принадлежат. Разобьем область определения функции на интервалы  .
.


 .
. .
. .
. 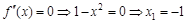 и
и  . Критические точки второго рода
. Критические точки второго рода  . Разобьем область определения функции на интервалы
. Разобьем область определения функции на интервалы  .
.


 .
. ,
,  .
. . Критических точек второго рода нет, поэтому нет точек перегиба (не выполнен необходимый признак). Так как
. Критических точек второго рода нет, поэтому нет точек перегиба (не выполнен необходимый признак). Так как  , то график функции выпуклый вниз. ▼
, то график функции выпуклый вниз. ▼ , не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.
, не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика. называется асимптотой кривой
называется асимптотой кривой  , если расстояние
, если расстояние 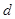 от точки
от точки  кривой
кривой 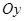 ), горизонтальные (параллельные оси
), горизонтальные (параллельные оси 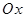 ) и наклонные (не параллельные ни одной из координатных осей).
) и наклонные (не параллельные ни одной из координатных осей).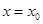 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 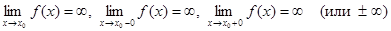 .
.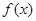 ;
;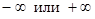 . Пусть это будут точки
. Пусть это будут точки 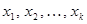 . Тогда прямые
. Тогда прямые 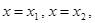
 будут вертикальными асимптотами графика функции
будут вертикальными асимптотами графика функции 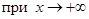 наклонную асимптоту
наклонную асимптоту  , необходимо и достаточно, чтобы существовали оба предела
, необходимо и достаточно, чтобы существовали оба предела .
. .
.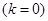 )
)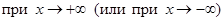 функция
функция  :
:  , то прямая
, то прямая 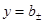 есть горизонтальная асимптота соответственно для правой или левой ветви графика функции
есть горизонтальная асимптота соответственно для правой или левой ветви графика функции 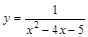 .
.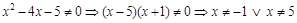 .
.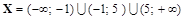 .
.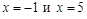 . Определим тип разрыва в этих точках, для чего вычислим пределы
. Определим тип разрыва в этих точках, для чего вычислим пределы 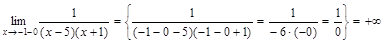 ,
,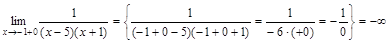 ,
,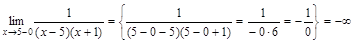 ,
,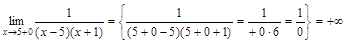 .
.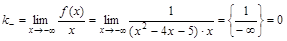 ;
; .
.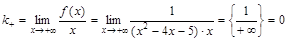 ;
;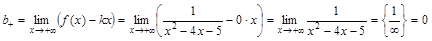 .
.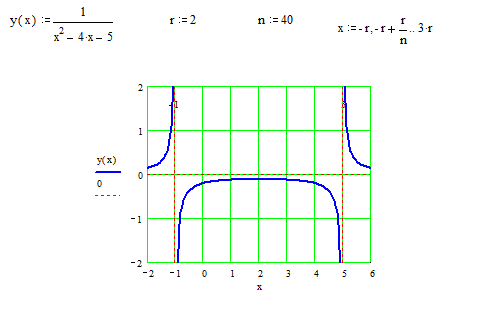 ▼
▼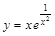 .
.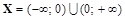 . Функция не определена в точке
. Функция не определена в точке 
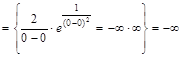
 .
.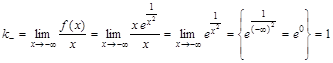 ,
,
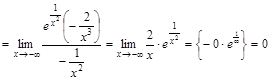 .
. – левая наклонная асимптота.
– левая наклонная асимптота. .
.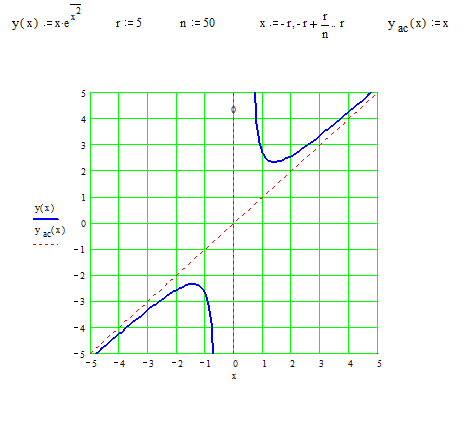 ▼
▼ .
.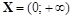 . Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем
. Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем .
.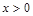 ):
):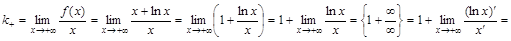
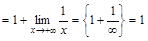 .
. .
. ▼
▼


