
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функции и построения ее графикаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Одна из возможных схем исследования функции и построения ее графика разлагается на следующие этапы решения задачи. Элементарное исследование 1. Найти область определения функции. 2. Найти точки разрыва функции. Их характер. Вертикальные асимптоты. 3. Исследовать функцию на симметричность (определить четность и нечетность функции) и периодичность. 4. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с осями координат. Найти интервалы знакопостоянства. 5. Вычислить предельные значения функции в ее граничных точках. 6. Выяснить существование наклонных асимптот. Исследование функции по первой производной 7. Найти решение уравнений 8. Критические точки, исследовать с помощью достаточного условия экстремума, определить вид экстремума. Вычислить значения функции в точках экстремума. 9. Найти интервалы монотонности функции. Исследование функции по второй производной 10. Найти решение уравнений 11. Критические точки исследовать с помощью достаточного условия. Вычислить значения функции в точках перегиба. 12. Найти интервалы выпуклости вниз и вверх графика функции. 13. Построить график функции. Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. График функции лучше всего строить в таком порядке: 1. Построить все асимптоты, если они есть. 2. Нанести на график характерные точки: точки пересечения с осями координат, точки, в которых есть экстремум, точки перегиба. Построение проводить в интервалах непрерывности с учетом проведенных исследований. Пример 13. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции. · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. В точке
в остальных точках она непрерывна. Прямая Найдем наклонные асимптоты Слева
Уравнение наклонной асимптоты слева Справа
Уравнение наклонной асимптоты справа · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью Точки пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
При переходе через точку Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 14. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции. · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. Вертикальных асимптот нет, так как нет точек разрыва. Найдем наклонные асимптоты Слева
Уравнение наклонной асимптоты слева Справа
Уравнение наклонной асимптоты справа · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью
Точки пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
При переходе через точки
Точки перегиба: Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 15. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции. · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. Вертикальных асимптот нет, так как нет точек разрыва. Найдем наклонные асимптоты Слева
Справа
Справа горизонтальная асимптота: · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью Точки пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
При переходе через точку Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 16. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. В точке
в остальных точках она непрерывна. Прямая Найдем наклонные асимптоты Слева
Уравнение горизонтальной асимптоты слева: Справа
Справа наклонной асимптоты нет. · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью Точки пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
Точек перегиба нет. Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 17. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции. · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. Вертикальная асимптота может существовать лишь на конечных границах области определения. Найдем
Значит, прямая Найдем
Следовательно, прямая Найдем наклонные асимптоты Слева
Уравнение горизонтальной асимптоты слева Справа
Уравнение горизонтальной асимптоты справа · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью
Точка пересечения с осью Точек пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Экстремумов нет. III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
К. т. II нет. Область определения функции разобьем на интервалы
Точек перегиба нет. Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

 .
. .
. и построить ее график.
и построить ее график. . Точка разрыва:
. Точка разрыва: 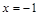 .
.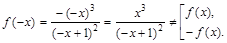 Функция общего вида.
Функция общего вида.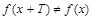 . Функция не периодична.
. Функция не периодична. ;
;  ,
,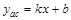 .
.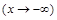 .
.
 .
. .
.
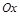 :
: 
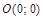 .
.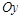 :
: 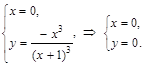
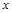
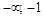
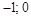
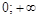


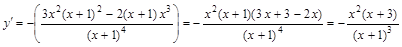 .
.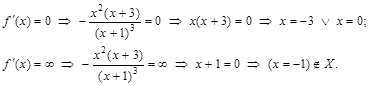
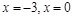 к. т. I.
к. т. I. и определим знак
и определим знак  в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом
в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом  ) с указанием поведения функции на этих интервалах занесем в таблицу:
) с указанием поведения функции на этих интервалах занесем в таблицу: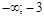

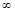
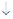
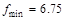


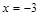 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее  .
.
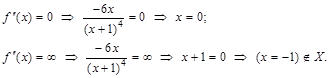
 к. т. II.
к. т. II. и определим знак
и определим знак  в каждом из них. Результат исследования знака функции
в каждом из них. Результат исследования знака функции 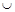

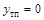
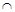
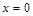 вторая производная меняет знак, следовательно, это точка перегиба функции, причем
вторая производная меняет знак, следовательно, это точка перегиба функции, причем 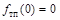 . Точка
. Точка  не является точкой перегиба.
не является точкой перегиба. ▼
▼ и построить ее график.
и построить ее график.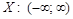 .
. Функция общего вида.
Функция общего вида. ,
,
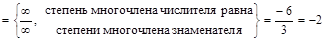 .
.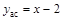 .
. ,
,
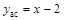 .
.
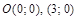 .
.
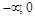


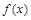
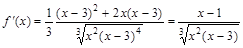 .
.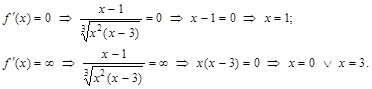
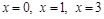 к. т. I.
к. т. I.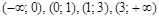 и определим знак
и определим знак 

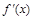
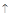
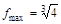
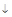
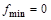
 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее 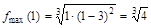 . В точке
. В точке 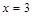 функция определена и непрерывна и при переходе через нее
функция определена и непрерывна и при переходе через нее 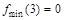 .
.
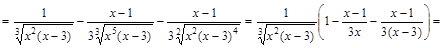

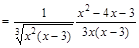 .
.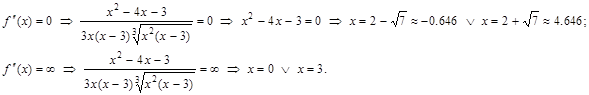
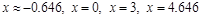 к. т. II.
к. т. II.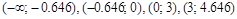 ,
,  и определим знак
и определим знак 
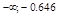
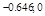


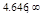
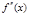
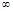
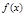

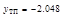

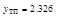
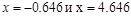 вторая производная меняет знак, следовательно, это точки перегиба функции, причем
вторая производная меняет знак, следовательно, это точки перегиба функции, причем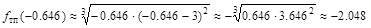 ,
,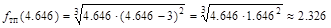 .
. .
.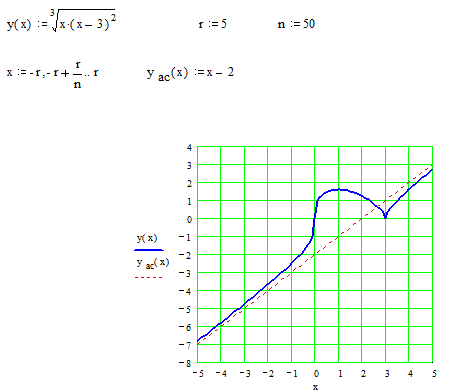 ▼
▼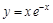 и построить ее график.
и построить ее график. .
.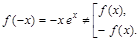 Функция общего вида.
Функция общего вида.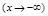 .
.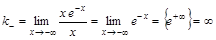 . Слева наклонной асимптоты нет.
. Слева наклонной асимптоты нет.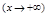 .
.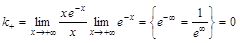 ,
,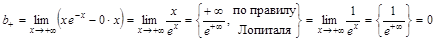 .
.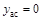 .
.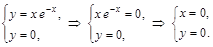
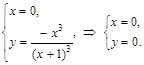
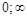
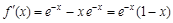 .
.
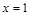 к. т. I.
к. т. I. и определим знак
и определим знак 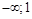

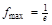
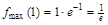 .
.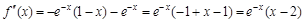 .
.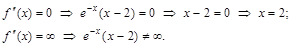
 к. т. II.
к. т. II. и определим знак
и определим знак 
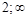
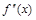

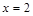 вторая производная меняет знак, следовательно, это точка перегиба функции, причем
вторая производная меняет знак, следовательно, это точка перегиба функции, причем 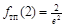 . Точка перегиба:
. Точка перегиба: 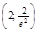 .
.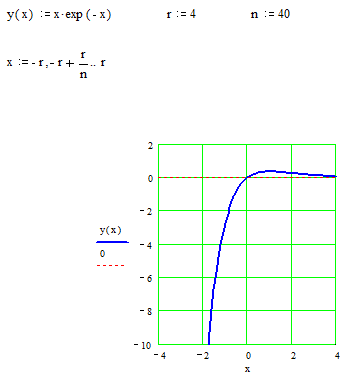 ▼
▼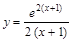 и построить ее график.
и построить ее график.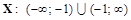 . Точка разрыва:
. Точка разрыва: 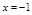 .
.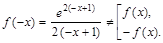 Функция общего вида.
Функция общего вида.
 ,
,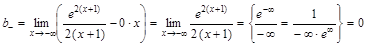 .
.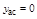 .
.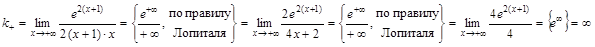 .
. Точек пересечения с осью
Точек пересечения с осью 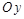 :
:  Точка пересечения с осью
Точка пересечения с осью  :
:  .
.
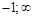

 .
.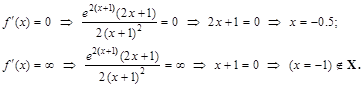
 к. т. I.
к. т. I. и определим знак
и определим знак 


 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее  .
.
 .
.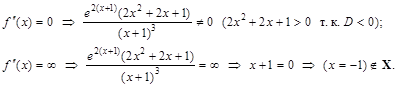 к. т. II нет.
к. т. II нет. и определим знак
и определим знак 
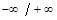

 и построить ее график.
и построить ее график. .
. Функция общего вида.
Функция общего вида. .
. .
. ,
, .
. .
. ,
,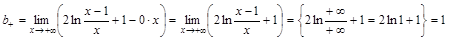 .
.
 .
.



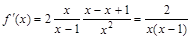 .
. к. т. I нет.
к. т. I нет. и определим знак
и определим знак  .
. ;
; .
.

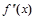

 ▼
▼


