
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К исследованию поведения функцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Р Г Г М У
Санкт-Петербург Одобрено Научно-методическим советом РГГМУ УДК 51 Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Применение дифференциального исчисления к исследованию поведения функций. – СПб.: Изд. РГГМУ. 2007. – 36 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок. Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н. © Российский государственный гидрометеорологический университет (РГГМУ), 2007.
ПРЕДИСЛОВИЕ
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями. Целью математического образования является: 1. Воспитание достаточно высокой математической культуры. 2. Привитие навыков современных видов математического мышления. 3. Привитие навыков использования математических методов и основ математического моделирования в практической деятельности. Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений. В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Применение дифференциального исчисления к исследованию поведения функций"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ПОВЕДЕНИЯ ФУНКЦИЙ Одной из важнейших прикладных задач дифференциального исчисления является разработка общих приемов исследования поведения функций. Основные теоретические сведения ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ Определение 1. Функция Определение 2. Функция Промежутки, на которых функция возрастает (убывает), называются промежутками монотонности. ПРИЗНАКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ Следующая теорема выражает важный для практических целей признак возрастания и убывания функции и указывает правило для определения интервалов, в которых функция возрастает и убывает (иначе, интервалов монотонности функций). При решении задач, в которых требуется определить интервалы возрастания и убывания функции, следует, прежде всего, определить область существования этой функции. Теорема 1 (достаточный признак возрастания и убывания функции на интервале). Если во всех точках некоторого интервала первая производная
|
||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.35.234 (0.007 с.) |


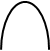


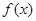 называется возрастающей в некотором интервале, если для любых двух чисел
называется возрастающей в некотором интервале, если для любых двух чисел 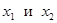 из этого интервала из неравенства
из этого интервала из неравенства 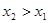 следует неравенство
следует неравенство  .
.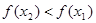 .
.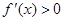 , то функция
, то функция  , то функция в этом интервале убывает.
, то функция в этом интервале убывает.


