
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение дифференциального исчисленияСодержание книги Поиск на нашем сайте УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ПОВЕДЕНИЯ ФУНКЦИЙ
Р Г Г М У
Санкт-Петербург Одобрено Научно-методическим советом РГГМУ УДК 51 Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Применение дифференциального исчисления к исследованию поведения функций. – СПб.: Изд. РГГМУ. 2007. – 36 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок. Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н. © Российский государственный гидрометеорологический университет (РГГМУ), 2007.
ПРЕДИСЛОВИЕ
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями. Целью математического образования является: 1. Воспитание достаточно высокой математической культуры. 2. Привитие навыков современных видов математического мышления. 3. Привитие навыков использования математических методов и основ математического моделирования в практической деятельности. Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений. В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Применение дифференциального исчисления к исследованию поведения функций"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ПОВЕДЕНИЯ ФУНКЦИЙ Одной из важнейших прикладных задач дифференциального исчисления является разработка общих приемов исследования поведения функций. Основные теоретические сведения ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИЙ Определение 1. Функция Определение 2. Функция Промежутки, на которых функция возрастает (убывает), называются промежутками монотонности. ЭКСТРЕМУМЫ ФУНКЦИИ Рассмотрим функцию Определение 3. Точка Определение 4. Точка Точки локального максимума и минимума называются точками локального экстремума, а значения в них – локальными экстремумами функции. Необходимое условие существования точек экстремума функции. Теорема 2.1. Для того чтобы точка Такие точки называются критическими, и они являются точками, подозрительными на экстремум. Достаточные условия экстремума. I. Теорема 2.2. Пусть функция 1) если 2) если 3) если II. Теорема 2.3. Пусть функция 1) минимум, если 2) максимум, если
y y
Проследите за изменением производной в зоне
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ Может оказаться, что размеры графика данной функции Определение. Прямая Различают три вида асимптот: вертикальные (параллельные оси Прямая
Для разыскания вертикальных асимптот кривой 1) находим на оси 2) выделяем те из них, в которых хотя бы один из пределов функции Наклонные асимптоты Теорема 4. Для того чтобы график функции
Аналогично для случая Горизонтальная асимптота (частный случай наклонной асимптоты Если Правило отыскания асимптот очевидно из следующего образца. Пример 10. Найти асимптоты кривой 1. ▲ Найдем область определения функции:
Функция не определена в точках
Следовательно, прямые 2. Найдем левую наклонную асимптоту:
Следовательно, имеем слева горизонтальную асимптоту Найдем правую наклонную асимптоту:
Значит, справа имеем горизонтальную асимптоту
Пример 11. Найти асимптоты кривой 1. ▲ Найдем область определения функции:
Аналогично получаем Прямая 2. Для нахождения левой наклонной асимптоты вычислим
Следовательно, прямая Аналогично для правой наклонной асимптоты получаем
Следовательно, прямая
Пример 12. Найти асимптоты кривой 1. ▲ Найдем область определения функции:
Значит, прямая 2. Найдем правую наклонную асимптоту (так как
Следовательно, наклонной асимптоты нет.
Элементарное исследование 1. Найти область определения функции. 2. Найти точки разрыва функции. Их характер. Вертикальные асимптоты. 3. Исследовать функцию на симметричность (определить четность и нечетность функции) и периодичность. 4. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с осями координат. Найти интервалы знакопостоянства. 5. Вычислить предельные значения функции в ее граничных точках. 6. Выяснить существование наклонных асимптот. Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
При переходе через точку Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 14. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции. · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. Вертикальных асимптот нет, так как нет точек разрыва. Найдем наклонные асимптоты Слева
Уравнение наклонной асимптоты слева Справа
Уравнение наклонной асимптоты справа · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью
Точки пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
При переходе через точки
Точки перегиба: Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 15. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции. · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. Вертикальных асимптот нет, так как нет точек разрыва. Найдем наклонные асимптоты Слева
Справа
Справа горизонтальная асимптота: · Определим точки пересечения графика функции с координатными осями, найдем интервалы знакопостоянства функции. Точки пересечения с осью Точки пересечения с осью Промежутки знакопостоянства
II. Исследование графика функции по первой производной. Для нахождения участков монотонности и экстремальных точек найдем первую производную функции:
Область определения функции разобьем на интервалы
Так как функция в точке III. Исследование графика функции по второй производной. Для нахождения участков выпуклости вверх и вниз найдем вторую производную функции
Область определения функции разобьем на интервалы
При переходе через точку Построение графика начнем с нанесения асимптот, точек пересечения с осями координат, экстремума, перегиба и фрагментов графика функции вблизи этих точек и асимптот. В окончательном виде график изображен на следующем рисунке.
Пример 16. Провести полное исследование функции ▲ Исследование функции будем проводить, придерживаясь приведенной выше схемы. I. Элементарное исследование · Область определения функции · Исследуем функцию на симметричность (определить четность и нечетность функции) и периодичность.
· Выясним существование асимптот. В точке
в остальных точках она непрерывна. Прямая Найдем наклонные асимптоты Слева
Уравнение горизонтальной асимптоты слева: Справа
Справа наклонной асимптоты нет. · Определим точки пересечения графика функции с координатными осями, найдем интервалы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 2302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |




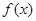 называется возрастающей в некотором интервале, если для любых двух чисел
называется возрастающей в некотором интервале, если для любых двух чисел 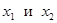 из этого интервала из неравенства
из этого интервала из неравенства 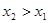 следует неравенство
следует неравенство  .
.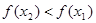 .
.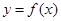 , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки  , включая и саму точку
, включая и саму точку 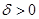 , что для всех
, что для всех 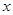 , удовлетворяющих условию
, удовлетворяющих условию  , верно неравенство
, верно неравенство  .
.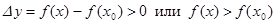 .
.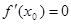 ; либо производная
; либо производная  не существует в точке
не существует в точке 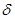 – окрестности точки
– окрестности точки 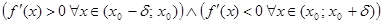 (т. е. при переходе
(т. е. при переходе  (т. е. при переходе
(т. е. при переходе  , то функция
, то функция 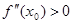 ,
,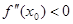 .
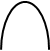
. Геометрический смысл необходимых и достаточных условий экстремумов
Геометрический смысл необходимых и достаточных условий экстремумов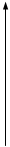
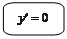



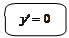

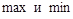 :
: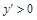 .
В точке
.
В точке 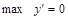 .
Справа функция убывает, т. е.
.
Справа функция убывает, т. е. 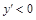 .
.
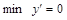 .
Справа функция возрастает, т. е.
.
Справа функция возрастает, т. е. 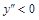
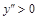
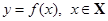 , не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.
, не ограничены. Это бывает, когда функция не ограничена или когда она задана на неограниченном промежутке. В таких случаях часто представление о графике функции вне рамок чертежа дают асимптоты графика.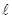 называется асимптотой кривой
называется асимптотой кривой 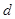 от точки
от точки  кривой
кривой 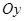 ), горизонтальные (параллельные оси
), горизонтальные (параллельные оси 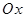 ) и наклонные (не параллельные ни одной из координатных осей).
) и наклонные (не параллельные ни одной из координатных осей).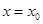 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 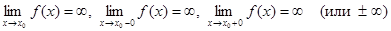 .
.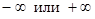 . Пусть это будут точки
. Пусть это будут точки 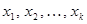 . Тогда прямые
. Тогда прямые 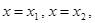
 будут вертикальными асимптотами графика функции
будут вертикальными асимптотами графика функции 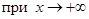 наклонную асимптоту
наклонную асимптоту  , необходимо и достаточно, чтобы существовали оба предела
, необходимо и достаточно, чтобы существовали оба предела .
. .
.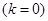 )
)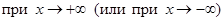 функция
функция  :
:  , то прямая
, то прямая 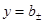 есть горизонтальная асимптота соответственно для правой или левой ветви графика функции
есть горизонтальная асимптота соответственно для правой или левой ветви графика функции 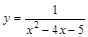 .
.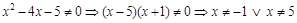 .
.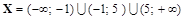 .
.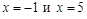 . Определим тип разрыва в этих точках, для чего вычислим пределы
. Определим тип разрыва в этих точках, для чего вычислим пределы 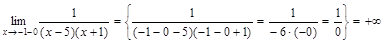 ,
,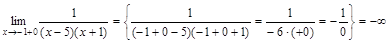 ,
,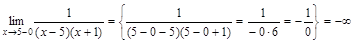 ,
,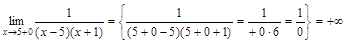 .
.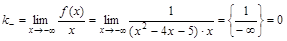 ;
; .
.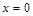 .
.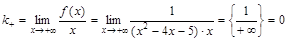 ;
;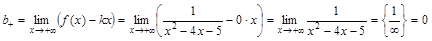 .
.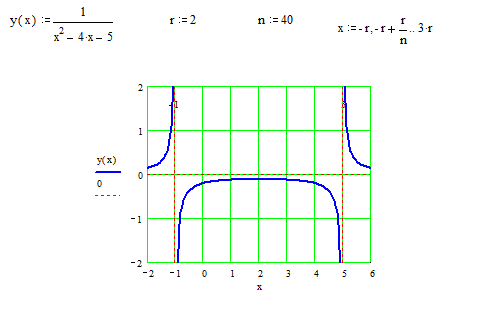 ▼
▼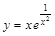 .
.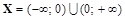 . Функция не определена в точке
. Функция не определена в точке 
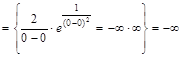
 .
.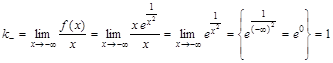 ,
,
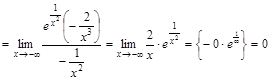 .
.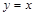 – левая наклонная асимптота.
– левая наклонная асимптота. .
.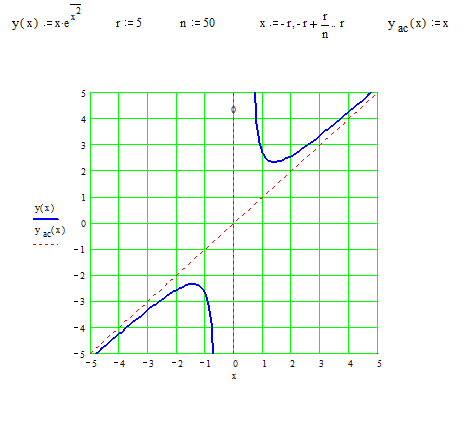 ▼
▼ .
.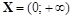 . Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем
. Поэтому вертикальная асимптота может существовать лишь на конечной границе области определения. Найдем .
.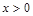 ):
):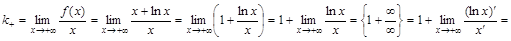
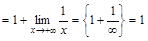 .
. .
.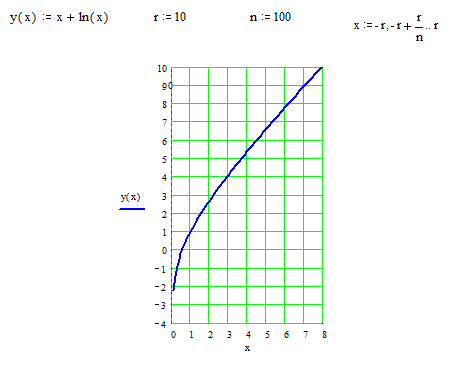 ▼
▼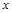
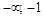
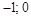
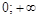


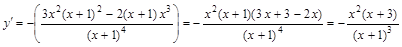 .
.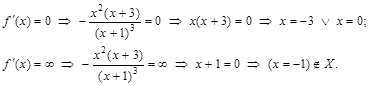
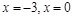 к. т. I.
к. т. I. и определим знак
и определим знак  в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом
в каждом из них (для удобства вычислений в каждом интервале выбираем фиксированную точку). Результаты исследования знака производной на интервалах между критическими точками (с учетом  ) с указанием поведения функции на этих интервалах занесем в таблицу:
) с указанием поведения функции на этих интервалах занесем в таблицу: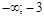

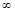
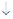
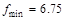


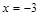 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее  .
.
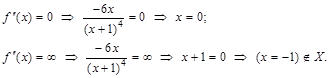
 к. т. II.
к. т. II. и определим знак
и определим знак  в каждом из них. Результат исследования знака функции
в каждом из них. Результат исследования знака функции 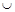

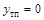
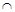
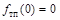 . Точка
. Точка  не является точкой перегиба.
не является точкой перегиба. ▼
▼ и построить ее график.
и построить ее график.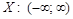 .
. Функция общего вида.
Функция общего вида.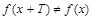 . Функция не периодична.
. Функция не периодична.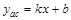 .
.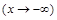 .
. ,
,
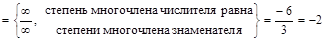 .
.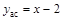 .
. .
. ,
,
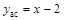 .
.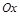 :
: 
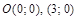 .
.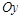 :
: 
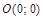 .
.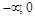


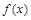
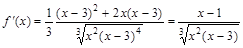 .
.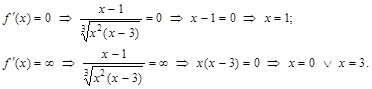
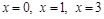 к. т. I.
к. т. I. и определим знак
и определим знак 

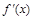
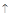
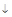
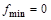
 определена и непрерывна и при переходе через нее
определена и непрерывна и при переходе через нее 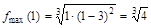 . В точке
. В точке 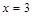 функция определена и непрерывна и при переходе через нее
функция определена и непрерывна и при переходе через нее 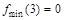 .
.
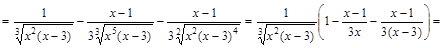

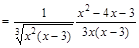 .
.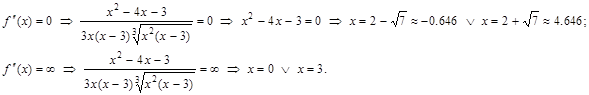
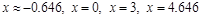 к. т. II.
к. т. II.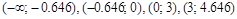 ,
,  и определим знак
и определим знак 
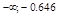
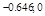


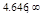
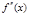
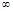
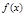

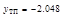

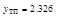
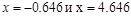 вторая производная меняет знак, следовательно, это точки перегиба функции, причем
вторая производная меняет знак, следовательно, это точки перегиба функции, причем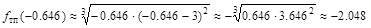 ,
,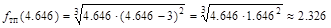 .
. .
.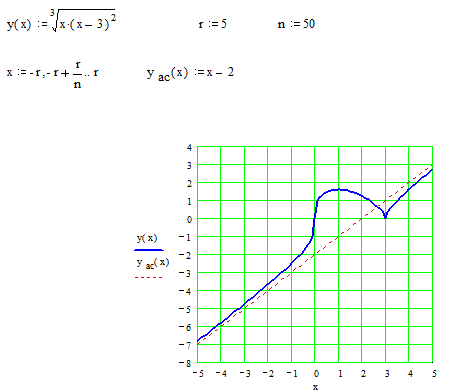 ▼
▼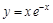 и построить ее график.
и построить ее график. .
.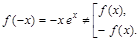 Функция общего вида.
Функция общего вида.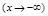 .
.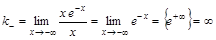 . Слева наклонной асимптоты нет.
. Слева наклонной асимптоты нет.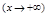 .
.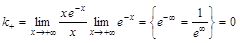 ,
,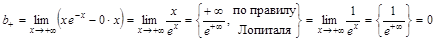 .
.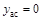 .
.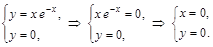
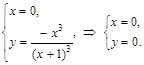
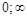
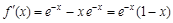 .
.
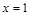 к. т. I.
к. т. I. и определим знак
и определим знак 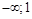

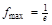
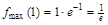 .
.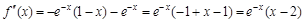 .
.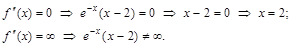
 к. т. II.
к. т. II. и определим знак
и определим знак 
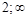
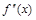

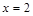 вторая производная меняет знак, следовательно, это точка перегиба функции, причем
вторая производная меняет знак, следовательно, это точка перегиба функции, причем 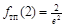 . Точка перегиба:
. Точка перегиба: 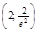 .
.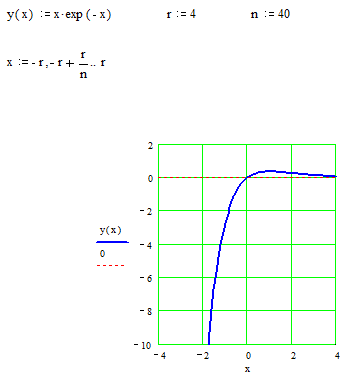 ▼
▼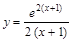 и построить ее график.
и построить ее график.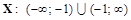 . Точка разрыва:
. Точка разрыва: 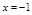 .
.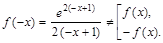 Функция общего вида.
Функция общего вида.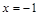 функция имеет разрыв II рода, ибо,
функция имеет разрыв II рода, ибо,
 ,
,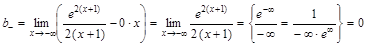 .
.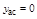 .
.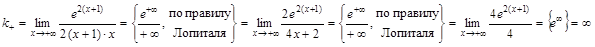 .
.


