Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический смысл условий монотонности.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Известно:
Практическое правило для нахождения промежутков монотонности функции. Для нахождения промежутков монотонности функции достаточно 1) разбить область существования функции 2) определить ее знак в каждом из этих интервалов. Для чего достаточно вычислить значение производной в какой-либо одной точке каждого интервала, ибо внутри каждого интервала производная Пример 1. Определить промежутки монотонности функции ▲ Функция определена на всей числовой оси Найдем ее первую производную: Эти точки разбивают область определения функции на интервалы Определим знак производной в каждом из интервалов, для чего достаточно вычислить знак Результаты исследования приведены в таблице.
Замечание. Условимся в дальнейшем возрастание, убывание функции на интервале обозначать так: Пример 2. Определить промежутки монотонности функции ▲ Функция определена на всей числовой оси Найдем ее первую производную: Этими точками разобьем область существования функции на интервалы Для определения знака производной в каждом интервале удобно взять точки
Пример 3. Определить промежутки монотонности функции ▲ Функция не определена Найдем ее первую производную: Этими точками разобьем область существования функции на интервалы Для определения знака производной в каждом интервале удобно взять точки
ЭКСТРЕМУМЫ ФУНКЦИИ Рассмотрим функцию Определение 3. Точка Определение 4. Точка Точки локального максимума и минимума называются точками локального экстремума, а значения в них – локальными экстремумами функции. Необходимое условие существования точек экстремума функции. Теорема 2.1. Для того чтобы точка Такие точки называются критическими, и они являются точками, подозрительными на экстремум. Достаточные условия экстремума. I. Теорема 2.2. Пусть функция 1) если 2) если 3) если II. Теорема 2.3. Пусть функция 1) минимум, если 2) максимум, если
y y
Проследите за изменением производной в зоне
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 2863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 – геометрический смысл производной (
– геометрический смысл производной ( угол между касательной и осью
угол между касательной и осью 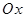 ).
).


 y y
y y
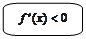






 O x0 x O x0 x
O x0 x O x0 x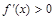 , так как касательная наклонена к оси
, так как касательная наклонена к оси  под острым углом
под острым углом  .
.
 , так как
касательная наклонена к оси
, так как
касательная наклонена к оси  .
.
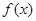 на интервалы точками, в которых ее первая производная
на интервалы точками, в которых ее первая производная  равна нулю или не существует,
равна нулю или не существует, ).
).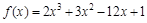 .
.
 . Она определена на всей числовой оси и равна нулю в точках
. Она определена на всей числовой оси и равна нулю в точках  (решается уравнение
(решается уравнение  ).
). .
. в какой-либо одной точке каждого интервала. Для первого интервала удобно взять
в какой-либо одной точке каждого интервала. Для первого интервала удобно взять  , следовательно, в интервале
, следовательно, в интервале  функция возрастает. Для второго интервала удобно взять
функция возрастает. Для второго интервала удобно взять 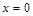 ,
,  , следовательно, в интервале
, следовательно, в интервале  функция убывает. Для третьего интервала
функция убывает. Для третьего интервала 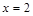 ,
, 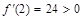 , следовательно, в интервале
, следовательно, в интервале  функция возрастает.
функция возрастает.



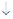
 .
. .
. . Производная не существует
. Производная не существует  и равна нулю
и равна нулю  .
. ,
,  .
. и
и  . Тогда
. Тогда 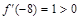 , следовательно, на интервале
, следовательно, на интервале  функция возрастает;
функция возрастает;  , значит, на интервале
, значит, на интервале  функция убывает;
функция убывает;  , значит, на интервале
, значит, на интервале  .
. , т. е. область определения функции
, т. е. область определения функции  .
. . Производная не существует
. Производная не существует  .
. ,
,  ,
,  . Тогда
. Тогда  , следовательно, на интервалах
, следовательно, на интервалах  , следовательно, на интервалах
, следовательно, на интервалах  функция убывает.
функция убывает.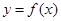 , определенную в некоторой окрестности точки
, определенную в некоторой окрестности точки  , включая и саму точку
, включая и саму точку 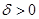 , что для всех
, что для всех 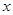 , удовлетворяющих условию
, удовлетворяющих условию  , верно неравенство
, верно неравенство  .
.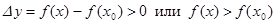 .
.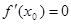 ; либо производная
; либо производная 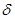 – окрестности точки
– окрестности точки 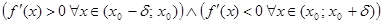 (т. е. при переходе
(т. е. при переходе  (т. е. при переходе
(т. е. при переходе  , то функция
, то функция 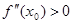 ,
,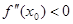 .
. Геометрический смысл необходимых и достаточных условий экстремумов
Геометрический смысл необходимых и достаточных условий экстремумов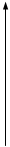
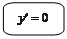



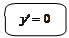

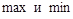 :
: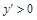 .
В точке
.
В точке 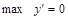 .
Справа функция убывает, т. е.
.
Справа функция убывает, т. е. 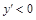 .
.
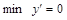 .
Справа функция возрастает, т. е.
.
Справа функция возрастает, т. е.