
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 2 Дифференциальное исчисление функций одного переменногоСодержание книги
Поиск на нашем сайте 1. Производная функции в точке. Касательная к графику функции, геометрический смысл производной. Вывод уравнений касательной и нормали к графику функции. 2. Дифференцируемость функции в точке. Теорема о связи дифференцируемости функции с существованием конечной производной (с доказательством). Связь дифференцируемости и непрерывности функции (с доказательством). 3. Основные правила дифференцирования. Вывод формул для вычисления производных суммы, произведения, частного. 4. Теорема о дифференцируемости сложной функции (формулировка). 5. Теорема о дифференцируемости обратной функции (формулировка). 6. Дифференциал функции (определение, геометрический смысл). Инвариантность формы записи дифференциала первого порядка (с доказательством) 7. Формулировки теорем Ферма, Ролля, Лагранжа, Коши. 8. Формулировка теоремы Бернулли – Лопиталя для предела отношения двух бесконечно малых функций. 9. Сравнение на бесконечности порядков роста показательной, степенной и логарифмических функций. 10. Формулы Тейлора с остаточным членом в форме Пеано и в форме Лагранжа (формулировка соответствующих теорем). 11. Формула Маклорена. Разложение по формуле Маклорена основных элементарных функций: 12. Необходимое и достаточное условия возрастания и убывания дифференцируемой функции (формулировка). 13. Понятие экстремума. Формулировка необходимого условия существования экстремума дифференцируемой функции. Формулировка достаточного условия существования экстремума функции по ее первой производной. Формулировка достаточного условия существования экстремума функции по ее второй производной. 14. Понятие выпуклой (вверх, вниз) функции (ее графика). Формулировка достаточного условия выпуклости дважды дифференцируемой функции. 15. Определение точек перегиба функции. Формулировка необходимого и достаточного условий для точек перегиба функции. 16. Асимптоты функции. Вывод уравнения наклонной асимптоты. Модуль 3 Итоговый контроль Формулировки определений и теорем, перечисленных выше в п. 1-35. Теоремы с изложением доказательства: 1. Теорема о единственности предела сходящейся последовательности. 2. Теорема о локальной ограниченности функции, имеющей конечный предел. 3. Теоремы о пределе суммы, произведения и частного функций (доказательство для функций или последовательностей по выбору). 4. Теорема о пределе сложной функции. 5. Теорема о знакопостоянстве функции, имеющей ненулевой предел. 6. Теорема о предельном переходе в неравенстве (доказательство для функций или последовательностей по выбору). 7. Теорема о пределе промежуточной функции (доказательство для функций или последовательностей по выбору). 8. Теорема о дифференцируемости сложной функции. 9. Теорема о дифференцируемости обратной функции. 10. Теорема Ферма. 11. Теорема Ролля. 12. Теорема Лагранжа. 13. Теорема Коши. 14. Теорема Бернулли – Лопиталя для предела отношения двух бесконечно малых функций. 15. Вывод формулы Тейлора с остаточным членом в форме Пеано и в форме Лагранжа (формулировка и доказательство соответствующих теорем). 16. Необходимое и достаточное условия возрастания и убывания дифференцируемой функции. 17. Достаточное условие локального экстремума функции по ее первой производной. 18. Достаточное условие локального экстремума функции по ее второй производной. 19. Достаточное условие выпуклости дважды дифференцируемой функции. 20. Необходимое условие для существования точек перегиба графика функции. 21. Достаточное условие для существования точек перегиба графика функции.
|
||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 ,
,  ,
,  ,
,  ,
, 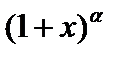 .
.


