
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовой экзаменационный билетСодержание книги
Поиск на нашем сайте 1. Докажите теорему о единственности предела сходящейся последовательности. 2. Докажите теорему Бернулли – Лопиталя для предела отношения двух бесконечно малых функций. 3. Вычислите предел 4. Исследуйте функцию Литература Основная литература (ОЛ) 1. Морозова В.Д. Введение в анализ. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 408 с. 2. Иванова Е.Е. Дифференциальное исчисление функций одного аргумента. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 408 с. 3. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. – 416 с. 4. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с Дополнительная литература (ДЛ)) 1. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч. 1. – 4-е изд., перераб. и доп. – М.: Наука, 1982. – 616 с. 2. Кудрявцев Л.Д. Курс математического анализа. В 3-х т. Т. 1. – М.: Высшая школа, 1988. – 718 с. 3. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – 431 с. 4. Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Астрель, 2003. – 472 с. 5. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. – М.: Эдиториал УРСС, 2000. – 328 с.
Методические пособия 1. Галкин С.В. Математический анализ. Методические указания по материалам лекций для подготовки к экзамену в первом семестре. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 116 с. 2. Грибов А.Ф., Котович А.В., Минеева О.М. Кривые на плоскости, заданные параметрически и в полярной системе координат. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 3. Казанджан Э.П. Исследование функций и построение графиков. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1995. 4. Ильичев А.Т., Кузнецов В.В., Фаликова И.Д. Графики элементарных функций. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 5. Соболев С. К., Ильичев А. Т. Исследование и построение плоских кривых, заданных параметрически и в полярных координатах. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 80 с. 6. Казанджан Э.П., Казанджан Г.П. Вычисление пределов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1995. 7. Кузнецов В.В., Коньков А.А., Соболев С.К. Множества и элементы математической логики. – М.: МГТУ, 1989. – 48 с. 8. Под ред. Ивановой Е.Е. Введение в анализ.-М., МГТУ, 1990.-85с. 9. Казанджан Г.П., Казанджан Э.П. Рабочий справочник по математике. – М., МГТУ, 2002. 10. Михайлова Т.Ю., Поляшова Р.Г., Титов К.В. Исследование свойств функций и построение графиков. Формула Тейлора и ее приложения. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 11. Казанджан Э.П. Графики. Сборник задач с примерами решений по исследованию функций и построению графиков. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 12. Дуров В.В., Мастихин А.В., Савин А.С. Пределы и непрерывность функций. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. – 62 с. Рекомендуемые Интернет-сайты: 1. Иванков П.Л. Конспект лекций по математическому анализу // http://mathmod.bmstu.ru/
МАТЕМАТИЧЕСКИЙ АНАЛИЗ для студентов, обучающихся по направлению 231300 (ФН2) ЛИТЕРАТУРА Основная литература (ОЛ) 1. Морозова В.Д. Введение в анализ. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2005. – 408 с. 2. Иванова Е.Е. Дифференциальное исчисление функций одного аргумента. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 408 с. 3. Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Астрель, 2003. – 472 с.
Дополнительная литература (ДЛ) 1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. – 416 с. 2. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1. – М.: ФИЗМАТЛИТ, 2003. – 680 с. 3. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с. 4. Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.1. – М.: Наука, 1982. – 616 с. 5. Кудрявцев Л.Д. Курс математического анализа. Т. 1. – М.: Высш. школа, 1988. – 718 с. 6. Вся высшая математика: Учебник для втузов / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко и др. Т. 1. – М.: Эдиториал УРСС, 2000. – 328 с. 7. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1988. – 431 с.
|
||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

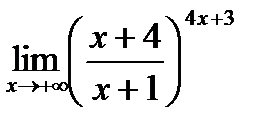 .
. и постройте ее график.
и постройте ее график.


