
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые задачи, используемые при формированииСодержание книги
Поиск на нашем сайте вариантов текущего контроля 1. Домашнее задание №1. «Векторная алгебра и аналитическая геометрия» Дано: точки Задание: Часть 1: 1. Найти длину вектора 2. Найти координаты точки М, делящей вектор 3. Проверить, можно ли на векторах 4. Найти углы между диагоналями параллелограмма ABCD. 5. Найти площадь параллелограмма ABCD. 6. Убедиться, что на векторах 7. Найти координаты вектора 8. Найти разложение вектора 9. Найти проекцию вектора Часть 2: 10. Написать уравнения плоскостей: а) P, проходящей через точки A, B, D; б) P1, проходящей через точку A и прямую A1B1; в) P2, проходящей через точку A1 параллельно плоскости P; г) P3, содержащей прямые AD и AA1; д) P4, проходящей через точки A и C1, перпендикулярно плоскости P. 11. Найти расстояние между прямыми, на которых лежат ребра AB и CC1; написать канонические и параметрические уравнения общего к ним перпендикуляра. 12. Найти точку A2, симметричную точке A1 относительно плоскости основания ABCD. 13. Найти угол между прямой, на которой лежит диагональ A1C, и плоскостью основания ABCD. 14. Найти острый угол между плоскостями ABC1D (плоскость P) и ABB1A1 (плоскость P1). 2. Домашнее задание №2. «Кривые и поверхности второго порядка» В задачах 1–2 заданное уравнение линии второго порядка привести к каноническому виду и построить кривую в системе координат OXY. В задаче 3 по приведенным данным найти уравнение кривой в системе координат OXY. Для задач 1–3 указать: 1) канонический вид уравнения линии; 2) преобразование параллельного переноса, приводящее к каноническому виду; 3) в случае эллипса: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов; в случае гиперболы: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов, уравнения асимптот; в случае параболы: параметр, вершину, фокус, уравнение директрисы, расстояния от точки C до фокуса и директрисы; 4) для точки C проверить свойство, характеризующее данный тип кривых как геометрическое место точек. В задаче 4 указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат OXYZ. 1) 3) Парабола симметрична относительно прямой 4) Контроль по модулю №1 “Векторная алгебра. Аналитическая геометрия” 1. Правые и левые тройки векторов. Определение векторного произведения векторов. Сформулировать свойства векторного произведения векторов. Вывести формулу вычисления векторного произведения двух векторов, заданных своими координатами в ортонормированном базисе. 2. Найти угол 3. Найти, если это возможно, разложение вектора 4. Составить уравнение плоскости, проходящей через точки
|
||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 1068; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 ,
, 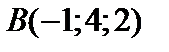 ,
,  ,
,  ; числа
; числа 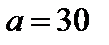 ,
,  ; угол
; угол  .
.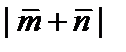 , если
, если 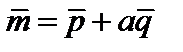 ,
,  и
и 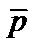 ,
,  — единичные векторы, угол между которыми равен
— единичные векторы, угол между которыми равен  .
. в отношении
в отношении  .
. и
и 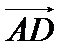 построить параллелограмм. Если да, то найти длины сторон параллелограмма.
построить параллелограмм. Если да, то найти длины сторон параллелограмма. ,
,  ,
,  можно построить параллелепипед. Найти объем этого параллелепипеда и длину его высоты.
можно построить параллелепипед. Найти объем этого параллелепипеда и длину его высоты. , направленного по высоте параллелепипеда
, направленного по высоте параллелепипеда  , проведенной из точки A к плоскости основания
, проведенной из точки A к плоскости основания  , координаты точки H и координаты единичного вектора, совпадающего по направлению с вектором
, координаты точки H и координаты единичного вектора, совпадающего по направлению с вектором  .
. по векторам
по векторам  ,
,  ,
,  .
. на вектор
на вектор  .
. ,
,  ; 2)
; 2)  ,
,  .
. , имеет фокус
, имеет фокус 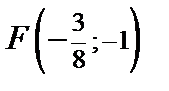 , пересекает ось OX в точке
, пересекает ось OX в точке  , а ее ветви лежат в полуплоскости
, а ее ветви лежат в полуплоскости  .
. .
. между векторами
между векторами 
 если
если 
 по векторам
по векторам  и
и 
 ,
,  и перпендикулярной плоскости
и перпендикулярной плоскости  Составить канонические уравнения прямой, проходящей через точку
Составить канонические уравнения прямой, проходящей через точку  и ортогональной к найденной плоскости.
и ортогональной к найденной плоскости.


