Модуль 1. Элементарные функции и пределы

 

Лекция 1-2. Введение в курс. Элементы логики. Высказывания и предикаты, операции над ними. Кванторы. Построение отрицания сложного высказывания. Теорема как импликация. Необходимость и достаточность. Прямая, обратная и противоположная теоремы, связь между ними. Доказательство от противного. Метод математической индукции. Неравенство Бернулли. Бином Ньютона. Множества, операции над ними, их свойства. Множество R действительных чисел и его аксиоматика. Полнота множества R. Промежутки. Окрестности конечной точки и бесконечности. Принцип вложенных отрезков (Коши-Кантора). Ограниченные и неограниченные множества в R. Точные верхняя и нижняя грани множества. Принцип Архимеда и следствия из него.

ОЛ-1 гл. 1;

ДЛ-2 Введение.

 

Лекция 3. Отображение и функция. График функции. Виды отображений: сюръективное, инъективное, биективное. Обратное отображение. Понятие мощности множества. Счетные множества. Несчетность множества R. Композиция функций. Числовые функции одного действительного переменного и их свойства: ограниченность, монотонность, четность, периодичность. Основные элементарные функции и их свойства.

ОЛ-1 гл. 2, 3;

ДЛ-1 гл. I §§ 6–9;

ДЛ-2 гл. 2 § 1.

 

Лекция 4. Числовая последовательность, ее ограниченность и монотонность. Предел последовательности. Бесконечно малая и бесконечно большая последовательности. Свойства сходящихся последовательностей. Теорема Вейерштрасса.

ОЛ-1 пп. 6.1–6.5, 6.7;

ДЛ-2 гл. 1 § 1, § 3 (п. 34, 35).

 

Лекции 5. Теорема об арифметических операциях под знаком предела. Число е как предел числовой последовательности. Гиперболические функции. Предельные точки множества. Принцип Больцано-Вейерштраса. Предельные точки последовательности. Фундаментальная числовая последовательность. Критерий Коши сходимости числовой последовательности.

ОЛ-1 пп. 6.6, д.6.1, д.6.2.;

ДЛ-2 гл. 1 § 2 (п. 30), § 3 (п. 36, 37), § 4.

 

Лекция 6. Определение предела функции по Коши. Теорема о связи двустороннего предела с односторонними. Определение предела функции по Гейне. Эквивалентность определений предела по Гейне и Коши (без доказательства). Теорема о единственности предела функции. Теорема о локальной ограниченности функции, имеющей конечный предел.

ОЛ-1 пп. 7.1–7.4;

ДЛ-1 гл. II, §§ 2–3;

ДЛ-2 гл. 2 § 2 (п. 52–56).

 

Лекция 7. Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой. Свойства бесконечно малых функций. Теорема об арифметических операциях над функциями, имеющими предел. Теорема о пределе сложной функции (замена переменной в пределе). Теорема о знакопостоянстве функции, имеющей отличный от нуля предел. Предельный переход в неравенстве. Теорема о пределе промежуточной функции (теорема «о двух милиционерах»).

ОЛ-1 пп. 7.5–7.6;

ДЛ-1 гл. II §§ 4–5;

ДЛ-2 гл. 2 § 2 (п. 55–56).

 

Лекция 8. Бесконечно большие функции. Теорема о связи бесконечно больших и бесконечно малых функций. Первый замечательный предел и следствия из него. Второй замечательный предел и следствия из него. Теорема Вейерштрасса о пределе монотонной и ограниченной функции.

ОЛ-1 пп. 7.5, 7.7, 7.8;

ДЛ-1 гл. II §§ 6–7;

ДЛ-2 гл. 2 § 3 (п. 65), гл. 2 § 2 (п. 54–57).

 

Лекция 9. Сравнение бесконечно малых. Порядок малости, эквивалентные бесконечно малые, несравнимые бесконечно малые. Таблица эквивалентных бесконечно малых. Свойства эквивалентных бесконечно малых. Правила работы с «о малое». Сравнение бесконечно больших. Теоремы об эквивалентных бесконечно больших.

ОЛ-1 гл. 10;

ДЛ-1 гл. II § 11;

ДЛ-2 гл. 2 § 3 (п. 60–64).

 

Лекция 10. Непрерывность функции в точке. Различные определения непрерывности и их эквивалентность. Приращение аргумента, приращение функции. Непрерывность функции в интервале. Односторонняя непрерывность в точке. Непрерывность функции на отрезке. Свойства функций, непрерывных в точке (связь непрерывности с односторонней непрерывностью, локальная ограниченность, знакопостоянство, арифметические операции с непрерывными функциями, предельный переход, непрерывность сложной функции). Точки разрыва и их классификация.

ОЛ-1 пп. 9.1–9.3;

ДЛ-1 гл. II §§ 9–10;

ДЛ-2 гл. 2 § 4 (п. 66–70).

 

Лекция 11. Свойства функций, непрерывных на отрезке (теоремы о нулях, о промежуточных значениях, об ограниченности, о достижении точных граней непрерывной на отрезке функции). Непрерывность на отрезке монотонной функции, связь непрерывности, инъективности и строгой монотонности. Теорема о существовании обратной функции. Точки разрыва монотонной функции. Критерий непрерывности монотонной функции. Теорема о непрерывности обратной функции.

ОЛ-1 пп. 9.4–9.5, д.9.1, д.9.2;

ДЛ-2 гл. 2 § 5 (п. 80–85), § 4 (п. 71).

 

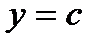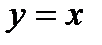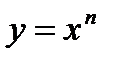Лекция 12. Непрерывность основных элементарных функций (, , , многочлен, дробно-рациональная функция, 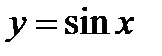, , , , 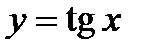, , 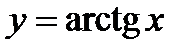, 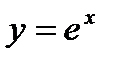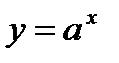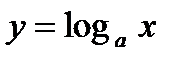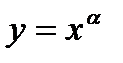). Равномерная непрерывность функций. Связь между равномерной непрерывностью на множестве и непрерывностью в точке этого множестве. Теорема Кантора о равномерной непрерывности функции на отрезке.

ОЛ-1 пп. 9.5, 5.9;

ДЛ-2 гл. 2 § 5 (п. 86–87), § 4 (п. 72–73).