
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая схема исследования функции иСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Построения ее графика Для качественного исследования графика функции y=f (x) целесообразно провести следующие исследования: 1. Найти область определения функции. 2. Выяснить вопрос о существовании асимптот (вертикальных и наклонных). 3. Найти области возрастания и убывания функции и точки экстремума. 4. Найти области сохранения направления выпуклости и точки перегиба графика. 5. Найти точки пересечения с осью Оx. Обычно по полученным данным легко строится эскиз графика.
В качестве примера построим график функции
1. Наша функция представляет собой рациональную дробь. Она определена при всех значениях х, при которых знаменатель не обращается в нуль. Область определения функции
2. Выясним, есть ли асимптоты.
Таким образом, имеется вертикальная асимптота х=0. А есть ли наклонная асимптота?
Итак, при
3. Для нахождения области возрастания и убывания вычислим первую производную
Имея в виду, что при х=0 функция и ее первая производная не существуют, составим таблицу, в которой отразим области сохранения знака первой производной
Из приведенной таблицы очевидно, что функция имеет следующие точки экстремума: 1) максимум при х= –3, при этом 2) максимум при х=1, 3) минимум при х=2, 4. Для нахождения областей сохранения выпуклости вычислим вторую производную
Составим таблицу сохранения знака
Из этой таблицы очевидно, что график функции имеет перегиб в точке
5. Найдем точки пересечения графика с осью Оx. Эти точки соответствуют вещественным корням уравнения
Наибольшее и наименьшее значение функции,
Непрерывной на отрезке Если функция y=f (x) непрерывна на замкнутом отрезке [ a,b ], то она достигает на нем своего наибольшего и наименьшего значений (в соответствии с теоремой Вейерштрасса). Наибольшее М и наименьшее m значения функции достигаются либо в критических точках, лежащих внутри отрезка (рис.1), либо на его концах (рис.2).
Возможны различные комбинации указанных случаев. Важно понять следующее: чтобы найти максимальное М и минимальное m значения при
Пример. Найти наибольшее и наименьшее значения функции
Ищем значения y (x) в трех точках: на концах интервала, т.е. при х= –1, х=2 и в критической точке х=1: y (–1)= –7; y (1)= 1; y (2)= 2. Итак: m= –7; M=2.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Примеры функций нескольких переменных
При изучении многих явлений приходится иметь дело с функциями двух и более переменных. Примеры: S=xy. S – площадь прямоугольника, х и у – длины его сторон. S есть функция двух переменных. V=xyz – объем прямоугольного параллелепипеда, длины ребер которого равны x, y, z. V – функция трех переменных.
x, y, z, t.
В дальнейшем мы будет рассматривать в основном функции двух переменных. Принципиальной разницы между функциями двух, трех и т.д. переменных нет, хотя технические трудности при вычислениях, безусловно, возрастают с ростом числа переменных.
3.2. Определение функции двух переменных. Область определения функции двух переменных
Определение 1. Если каждой паре (х, у) значений двух, независимых друг от друга переменных величин х и у из некоторой области их изменения D, соответствует определенное значение величины z, то z есть функция двух независимых переменных х и у, определенная в области D. Обозначение: z = f (x, y), z = F (x, y) и т.д.
Определение 2. Совокупность пар (х, у) значений х и у, при которых определена функция z = f (x, y), называется областью определения или областью существования этой функции.
Примеры. Найти область определения функций:
1. z = 2x – y. Выражение 2х – у имеет смысл при всех х и у. Следовательно, область определения D – вся плоскость хОу.
2. Область определения определяется неравенством 3. z = ln(x + y). Очевидно, х + у > 0, y >– x. Это полуплоскость над прямой у =– х (см. рис.).
Точки прямой у=–х в область D не входят.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.217.232 (0.009 с.) |


 (определена везде кроме точки х=0).
(определена везде кроме точки х=0).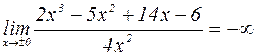

 и при
и при 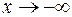 график имеет наклонную асимптоту
график имеет наклонную асимптоту 



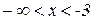






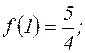


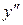 (заметим, что при х=0
(заметим, что при х=0  не существует).
не существует).



 При этом
При этом 
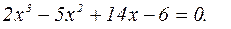 (*)
(*) а квадратный трехчлен
а квадратный трехчлен  имеет только комплексные корни
имеет только комплексные корни , то уравнение (*) имеет единственный вещественный корень
, то уравнение (*) имеет единственный вещественный корень  , т.е. график пересекает ось Оx только в точке
, т.е. график пересекает ось Оx только в точке  . По полученным данным строим эскиз графика.
. По полученным данным строим эскиз графика.

 , следует найти все критические точки внутри отрезка, а затем присоединить к ним две крайние точки отрезка: x=a и x=b, во всех точках вычислить значения функции и отобрать среди них наибольшее и наименьшее.
, следует найти все критические точки внутри отрезка, а затем присоединить к ним две крайние точки отрезка: x=a и x=b, во всех точках вычислить значения функции и отобрать среди них наибольшее и наименьшее.
 – функция четырех переменных
– функция четырех переменных
 или х2 + у2£1. Очевидно, D – точки круга радиуса 1 с центром в начале координат. Граница круга входит в область определения.
или х2 + у2£1. Очевидно, D – точки круга радиуса 1 с центром в начале координат. Граница круга входит в область определения.



