
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые множества вещественных чиселСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В математике множество относится к так называемым первичным, неопределяемым понятиям (в школьной математике такими первичными понятиями являются понятия числа, точки, прямой и т.д.). Под множеством понимается собрание или совокупность каких-либо предметов. Примеры: множество деревьев на поляне; множество всех целых чисел. Обозначаются множества обычно большими латинскими буквами: A, B,U и т.д. Если x – один из предметов множества A, то записывают так: В дальнейшем мы будем иметь дело с различными множествами действительных чисел. Наиболее часто используются следующие числовые множества, задаваемые с помощью неравенств:
1. 2. a<x<b, (a,b) – интервал; 3. 4. Любой интервал, содержащий точку C, называют ее окрестностью; 5. Интервал 6. Множество всех вещественных чисел будем называть бесконечной числовой прямой, обозначение: 7. 8.
Основные операции над множествами 1. Объединением множеств A и B называется множество 2. Пересечением множеств A и B называется множество 3. Разностью множеств A и B называется множество Запись Множества A и B называются равными, если
Множества вещественных чисел, ограниченные Сверху или снизу Рассмотрим произвольное множество
Определение. Множество вещественных чисел При этом число M (число m) называется верхней гранью (нижней гранью) множества Естественно, возникают вопросы: имеется ли среди верхних граней множества наименьшая? Или имеется ли среди нижних граней наибольшая?
Определение. Наименьшая из всех верхних граней ограниченного сверху множества Это определение можно сформулировать по другому. Число 1) Каждый элемент множества 2) Каково бы ни было вещественное число
Теорема. Если множество вещественных чисел содержит хотя бы один элемент и ограничено сверху (снизу), то существует вещественное число Формулировка этой теоремы дается без доказательства.
Понятие о функции Если каждому значению переменной x, принадлежащей некоторой области, соответствует одно определенное значение другой переменной y, то y есть функция от x. Символьная запись:
Определение. Совокупность значений x, для которых определяются значения y в силу правила f(x), называется областью определения (ОДЗ аргумента функции). Обозначается
Функцию можно задать: 1) таблицей:
Существуют, например, таблицы тригонометрических, логарифмических, показательных функций и т.д.
2) графически:
3) аналитически (формулой):
Теперь я напомню вам про основные элементарные функции, которые изучались в школьном курсе математики.
1. Степенная функция 2. Показательная функция 3. Логарифмическая функция 4. Тригонометрические функции 5. Обратные тригонометрические функции
Рассмотрим области определения и графики этих функций. Степенная функция 1. Область определения:
Примеры:
y
x
2.
2. Если а) Если q – нечетное, то область определения:
Примеры:
б) Если q – четное, то область определения:
Пример:
3. Если
а) Если q – нечетное, то область определения: Примеры:
б) Если q – четное, то область определения: x>0. Пример:
4. Если
Примеры:
6. Если Пример:
Показательная функция
Область определения:
а) 0<a<1 б) a>1
Логарифмическая функция Область определения x>0.
а) a>1 б) 0<a<1
Тригонометрические функции Аргумент x в тригонометрических функциях y=sinx, y=cosx и т.д. выражается в радианах. Углу в
Определение. Функция
Функция y=sinx определена при всех x. Ее график имеет вид:
Функция y=cosx также определена при всех x, а график ее изображен ниже:
Функция y=tgx определена при всех x, кроме точек
График имеет вид:
Функция y=ctgx определена при всех x, за исключением График имеет вид:
Обратные тригонометрические функции Функция y=arcsinx; область определения: График имеет вид:
Значения функции заполняют отрезок
Функция y=arccosx; область определения: График имеет вид:
Значения функции находятся на отрезке
Функция y=arctgx; область определения: График имеет вид:
Значения функции заполняют интервал Функция y=arcсtgx определена при всех x.
График имеет вид:
Значения функции находятся в интервале
Мы с вами рассмотрели основные элементарные функции. Все эти функции вы изучали в школе. Кроме основных элементарных функций в математике имеется понятие об элементарных функциях. Прежде, чем мы с ним познакомимся, введем вначале понятие сложной функции. Если y является функцией от u,
Пример:
Операция “функция от функции” может производиться не один, а любое число раз. Например, функция Теперь дадим определение элементарной функции.
Определение. Элементарной функцией называется функция, которая составлена из основных элементарных функций при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. На основании этого определения ясно, что элементарные функции задаются аналитически.
Пример элементарной функции:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 741; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

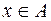 (x принадлежит A). Если какой-то элемент не принадлежит множеству A, то пишут так:
(x принадлежит A). Если какой-то элемент не принадлежит множеству A, то пишут так: 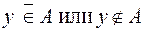 .
.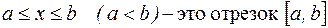 ; a и b – граничные точки отрезка; любое число a<x<b – это внутренняя точка отрезка;
; a и b – граничные точки отрезка; любое число a<x<b – это внутренняя точка отрезка; – полуинтервалы;
– полуинтервалы; называется
называется  -окрест-ностью точки C;
-окрест-ностью точки C; ;
;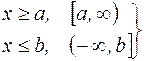 – полупрямые;
– полупрямые; – открытые полупрямые.
– открытые полупрямые. .
.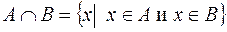 .
. .
. означает, что каждый элемент множества A является элементом множества B.
означает, что каждый элемент множества A является элементом множества B. (состоят из одних и тех же элементов).
(состоят из одних и тех же элементов). вещественных чисел, содержащее хотя бы одно число. Отдельные числа этого множества будем называть его элементами.
вещественных чисел, содержащее хотя бы одно число. Отдельные числа этого множества будем называть его элементами.
 , так же, как и M, является верхней гранью. Аналогичное замечание можно сделать относительно нижней грани.
, так же, как и M, является верхней гранью. Аналогичное замечание можно сделать относительно нижней грани. – супремум. Наибольшая из всех нижних граней ограниченного снизу множества
– супремум. Наибольшая из всех нижних граней ограниченного снизу множества  – инфинум.
– инфинум.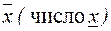 называется точной верхней (точной нижней) гранью множества
называется точной верхней (точной нижней) гранью множества 
 , меньшее
, меньшее 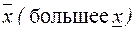 , найдется хотя бы один элемент x множества
, найдется хотя бы один элемент x множества  (
( ).
).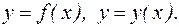
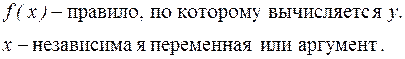
 .
.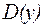 – множество значений, которые принимает функция
– множество значений, которые принимает функция 
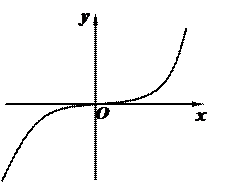
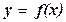
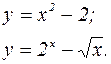
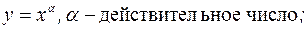

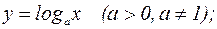
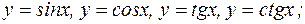
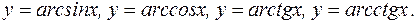
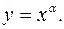
 целое положительное число.
целое положительное число.
 (парабола)
(парабола) 
 y y
y y
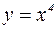


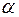 – целое отрицательное число. Область определения:
– целое отрицательное число. Область определения: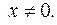

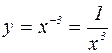




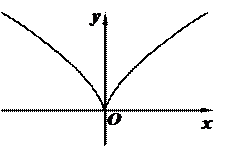
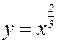





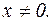








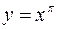



 . Напомню, что a>0,
. Напомню, что a>0, 





 Все тригонометрические функции – периодические. Дадим общее определение периодической функции.
Все тригонометрические функции – периодические. Дадим общее определение периодической функции. называется периодической, если существует такое постоянное число T, от прибавления (вычитания) которого к аргументу x значение функции не меняется:
называется периодической, если существует такое постоянное число T, от прибавления (вычитания) которого к аргументу x значение функции не меняется:  Наименьшее такое число называется периодом функции. Напомню, что период функций y=sinx и y=cosx
Наименьшее такое число называется периодом функции. Напомню, что период функций y=sinx и y=cosx 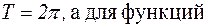 y=tgx и y=ctgx
y=tgx и y=ctgx 


 Z – множество всех целых чисел.
Z – множество всех целых чисел.
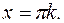











 , а u в свою очередь зависит от переменной x,
, а u в свою очередь зависит от переменной x, 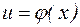 , то y также зависит от x. Эта зависимость записывается так:
, то y также зависит от x. Эта зависимость записывается так: 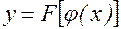 ; y является сложной функцией от x.
; y является сложной функцией от x. – сложная функция.
– сложная функция.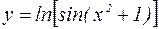 получена в результате следующих операций:
получена в результате следующих операций: 
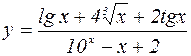 .
.


