
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отыскание точек возможного экстремумаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мы ввели понятия локального экстремума (локального максимума и локального минимума). Напомню: если функция определена в окрестности точки с и f (с) является наибольшим значением в этой окрестности, то точка с – точка локального максимума. Если же f (с) – наименьшее значение в указанной окрестности, то с – точка локального минимума. Если функция дифференцируема и имеет в точке с экстремум (max или min), то Экстремум, однако, может быть, а может его и не оказаться. Достаточным же условием экстремума является смена знака у производной Производная может не изменять знака при переходе через стационарную точку: в этом случае экстремума (максимума или минимума) нет.
Примеры. 1. Возьмем предыдущий пример
х=0 и х=2 – стационарные точки. Мы уже видели, что при Поэтому слева от точки х=0 Аналогично слева от точки х=2 2. Очевидно
График имеет вид:
Если исследовать знак первой производной слева и справа от стационарной точки затруднительно, то можно установить наличие или отсутствие экстремума по второй производной в критической точке (разумеется, если эта вторая производная
Пример. Опять возьмем
В первой критической точке х=0 Во второй критической точке х=2 Экстремум функции, не дифференцируемой в данной точке До сир пор мы решали вопрос о наличии у функции f (x) экстремума в такой точке с, в которой функция f (x) дифференцируема. Теперь изучим вопрос о наличии экстремума в точке с, в которой функция не дифференцируема, но дифференцируема всюду в некоторой окрестности справа и слева от точки с.
Теорема. Пусть функция f (x) дифференцируема всюду в некоторой окрестности точки с, за исключением, быть может, самой точки с, и непрерывна в точке с. Тогда, если в пределах указанной окрестности производная Если же производная имеет слева и справа от с одинаковый знак, то экстремума в точке с нет (без доказательства).
Графическая иллюстрация:
В случаях 1 и 2 производная меняет в точке с знак; в случае 1 с «+» на «–», функция имеет max; в случае 2 с «–» на «+», функция имеет min. В случае 3 Выпуклость и вогнутость кривой. Точки Перегиба Предположим, что функция f (x) дифференцируема в любой точке интервала (a,b). Тогда в каждой точке имеется касательная к графику, причем она не параллельна оси Оy (ибо ее угловой коэффициент
Определение. Будем говорить, что график функции y=f (x) имеет на интервале (a,b) выпуклость, направленную вниз (кривая вогнутая), если график в пределах интервала лежит не ниже любой своей касательной. Если график лежит не выше любой своей касательной, будем говорить, что график имеет выпуклость, направленную вверх (кривая выпуклая).
Вогнутая кривая Выпуклая кривая (выпуклость направлена вниз) (выпуклость направлена вверх) Теорема. Если функция y=f (x) имеет на интервале (a,b) конечную вторую производную и если эта производная не отрицательна (не положительна) всюду на этом интервале, то график функции y=f (x) имеет на интервале (a,b) выпуклость, направленную вниз (вверх). Мнемоническое правило. Если в сосуд набирается вода, то «+»,
Доказательство.
Для определенности рассмотрим случай, когда
Требуется доказать, что график функции f (x) лежит не ниже касательной, проходящей через точку
Разложим f (x) в окрестности точки с по формуле Тейлора, взяв в этой формуле два члена (n=2):
Здесь учтен остаточный член
Поскольку А это и означает, что график функции y=f (x) находится не ниже, чем касательная. Аналогично доказывается случай, когда Итак, что же мы получили? Направление выпуклости графика функции полностью характеризуется знаком второй производной этой функции. Таким образом, первая производная определяет, в каких точках имеется максимум или минимум и на каких интервалах функция возрастает или убывает, а вторая производная определяет те интервалы, на которых функция выпукла вверх или вниз.
Точки перегиба графика функции Определение. Точка Пример. Рассмотрим график y=sinx.
На интервале Оказывается, что для этого графика все точки
Теорема (необходимые условия перегиба) (без доказательства). Если функция f (x) имеет в точке с вторую производную
Пример.
Пример, иллюстрирующий, что условие
В точке х=0 перегиба нет.
Поэтому надо иметь достаточный признак существования перегиба графика. Теорема (достаточное условие перегиба). Пусть функция y=f (x) имеет вторую производную в некоторой окрестности точки с и Теперь все встало на свои места: смена знака первой производной определяет наличие экстремума, а смена знака второй производной определяет наличие перегиба графика.
Асимптоты графика функции
Определение 1.
Пример. 1) х=0 – вертикальная асимптота.
2) y=lnx; х=0 – вертикальная асимптота.
Определение 2. Прямая y=kx+b (*) является наклонной асимптотой графика функции y=f (x) при
Теорема. Для того, чтобы график функции y=f (x) имел при
Аналогично определяется асимптота при
Пример.
При Кроме того, при
Имеется вертикальная асимптота х= –1. График функции
Если оба предела:
Пример.
Таким образом,
левую у= –1 и правую у=1. График выглядит так:
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1071; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.180.236 (0.007 с.) |

 Таким образом, для отыскания у дифференцируемой функции точек возможного экстремума следует найти все корни уравнения
Таким образом, для отыскания у дифференцируемой функции точек возможного экстремума следует найти все корни уравнения  т.е. найти все нули производной
т.е. найти все нули производной  . Эти точки называются точками возможного экстремума (стационарными точками).
. Эти точки называются точками возможного экстремума (стационарными точками).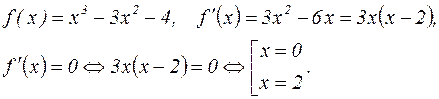
 , при
, при 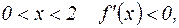

 , справа
, справа 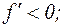 х=0 – точка max.
х=0 – точка max. , а справа
, а справа 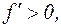 х=2 – точка min (см. график).
х=2 – точка min (см. график).
 при х=2. Если же
при х=2. Если же 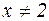 , то
, то  , т.е. слева и справа от точки х=2 производная положительна. Экстремума нет.
, т.е. слева и справа от точки х=2 производная положительна. Экстремума нет.
 существует).
существует). . Тогда
. Тогда
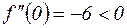 отрицательный знак указывает, что
отрицательный знак указывает, что 
 в точке х=2 возрастает, т.е. меняет знак с «-» на «+». Точка х=2 – точка min.
в точке х=2 возрастает, т.е. меняет знак с «-» на «+». Точка х=2 – точка min. (х) положительна (отрицательна) слева от точки с и отрицательна (положительна) справа от точки с, то функция имеет в точке с локальный максимум (минимум).
(х) положительна (отрицательна) слева от точки с и отрицательна (положительна) справа от точки с, то функция имеет в точке с локальный максимум (минимум).
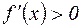 и слева и справа от точки с; экстремума нет. Аналогично в случае 4
и слева и справа от точки с; экстремума нет. Аналогично в случае 4  и слева и справа от точки с; экстремума также нет.
и слева и справа от точки с; экстремума также нет. конечен).
конечен). Примеры.
Примеры. выпуклость направлена вниз. Если вода не набирается,
выпуклость направлена вниз. Если вода не набирается,  то знак «–», выпуклость направлена вверх.
то знак «–», выпуклость направлена вверх.
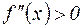 всюду на (a,b). Обозначим через c любую точку интервала (a,b) (см. рис.).
всюду на (a,b). Обозначим через c любую точку интервала (a,b) (см. рис.).
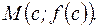 Запишем уравнение касательной, проходящей через точку М:
Запишем уравнение касательной, проходящей через точку М: (1)
(1) (2)
(2) в форме Лагранжа;
в форме Лагранжа; 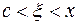 . Поскольку по условию
. Поскольку по условию  существует всюду на (a,b), формула (2) справедлива для любого
существует всюду на (a,b), формула (2) справедлива для любого  . Вычитая из (2) (1), получим:
. Вычитая из (2) (1), получим:
 всюду на (a,b), то
всюду на (a,b), то 

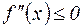 .
. графика функции y=f (x) называется точкой перегиба этого графика, если существует такая окрестность точки с, в пределах которой график слева и справа от точки с имеет разные направления выпуклости.
графика функции y=f (x) называется точкой перегиба этого графика, если существует такая окрестность точки с, в пределах которой график слева и справа от точки с имеет разные направления выпуклости.
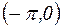 функция y=sinx имеет выпуклость, направленную вниз, на интервале
функция y=sinx имеет выпуклость, направленную вниз, на интервале 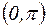 выпуклость направлена вверх, точка х=0 – точка перегиба графика.
выпуклость направлена вверх, точка х=0 – точка перегиба графика. – точки перегиба.
– точки перегиба.
 если x<0, то
если x<0, то  , выпуклость графика направлена вверх. Если x>0, то
, выпуклость графика направлена вверх. Если x>0, то 


 не является достаточным условием перегиба:
не является достаточным условием перегиба: 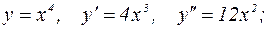
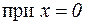
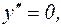 но перегиба нет, т.к.
но перегиба нет, т.к.  при всех х. График имеет вид:
при всех х. График имеет вид:
 но
но Тогда, если в пределах указанной окрестности вторая производная
Тогда, если в пределах указанной окрестности вторая производная  Прямая х=а является вертикальной асимптотой графика функции y=f (x), если хотя бы одно из предельных значений
Прямая х=а является вертикальной асимптотой графика функции y=f (x), если хотя бы одно из предельных значений 


 , если функция f (x) представима в виде
, если функция f (x) представима в виде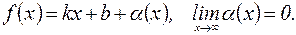
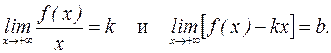
 Если хотя бы один из этих пределов не существует или бесконечен, то соответствующей асимптоты нет.
Если хотя бы один из этих пределов не существует или бесконечен, то соответствующей асимптоты нет.

 имеется наклонная асимптота Y=2x–1.
имеется наклонная асимптота Y=2x–1.

 выглядит так:
выглядит так:
 существуют, но k=0, это означает, что имеет место не наклонная, а горизонтальная асимптота.
существуют, но k=0, это означает, что имеет место не наклонная, а горизонтальная асимптота.

 функция имеет две горизонтальные асимптоты:
функция имеет две горизонтальные асимптоты:



