
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глобальный и условный экстремумыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Множители Лагранжа. Другой способ определения условного экстремума начинается с построения вспомогательной функции Лагранжа, которая в области допустимых решений достигает максимума для тех же значений переменных Пусть решается задача определения условного экстремума функции Составим функцию: Отметим, что множителям Лагранжа можно придать экономический смысл. Если
Определение стационарных точек этой функции приводит к решению системы уравнений: Легко заметить, что Таким образом, определение экстремальных точек методом Лагранжа включает следующие этапы: 1. Составляют функцию Лагранжа. 2. Находят частные производные от функции Лагранжа и приравнивают их нулю. 3. Решая систему уравнений (47.2), находят точки, в которых целевая функция задачи может иметь экстремум. 4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычисляют значение функции в этих точках. Пример. Определить точки экстремума Решение. Составим линейная система уравнений. Применяя метод Крамера, получим: Функция
Задача о потребительском выборе. В теории потребления предполагается, что потребитель всегда стремится максимизировать свою полезность и ограничением для него является величина дохода В общем, задача потребительского выбора (задача рационального поведения потребителя на рынке) записывается следующим образом: найти такой потребительский набор Задачу потребительского выбора (для n- мерного набора) можно записать в виде:
Задача потребительского выбора (для случая набора из двух товаров): найти такой набор
Рис. 48.1 Поиск оптимального набора Таким образом, задача потребительского выбора сводится к задаче на условный экстремум функций двух переменных: найти точку Второе уравнение выражения называется уравнением связи. Для решения задачи используем метод Лагранжа. Составим функцию Лагранжа:
где l - множитель Лагранжа. Из (48.3) следует экономический смысл множителя Лагранжа: если цены и доход меняются в одно и то же число раз l, то функция полезности и решение задачи потребительского выбора не изменятся. Для нахождения максимума функции
Исключив из этих уравнений l, получим систему двух уравнений с неизвестными Из системы находится точка Вернемся к n -мерному набору. Итак, точка
Составим функцию Лагранжа:
Для нахождения максимума функции
Исключив из уравнений множитель l, получим систему:
Решение системы Точка
Условная оптимизация. На первом этапе решения задачи, называемом условной оптимизацией, определяются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего, в соответствии с алгоритмом обратной прогонки. На последнем, n -м шаге оптимальное управление -
в соответствии с которой максимум выбирается из всех возможных значений Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге. В общем виде это уравнение имеет вид:
Этот максимум (или минимум) определяется по всем возможным для k и S значениям переменной управления Безусловная оптимизация. После того, как функция Беллмана и соответствующие оптимальные управления найдены для всех шагов с n- го по первый, осуществляется второй этап решения задачи, называемый безусловной оптимизацией. Пользуясь тем, что на первом шаге (k = 1) состояние системы известно - это ее начальное состояние S0 , можно найти оптимальный результат за все n шагов и оптимальное управление на первом шаге
Рис. 52.1 В задаче имеется ограничение - двигаться по изображенным на схеме маршрутам можно только слева на право, т.е. попав, например, в пункт 7, мы имеем право переместиться только в пункт 10 и не можем возвратиться обратно в 5 -й или 6 -й. Эта особенность транспортной сети дает право отнести каждый из десяти пунктов к одному из поясов. Будем считать, что пункт принадлежит k - му поясу, если из него попасть в конечный пункт ровно за k шагов, т.е. с заездом ровно в (k - 1)-й промежуточный пункт. Таким образом, пункты 7, 8 и 9 принадлежат к первому поясу, 5 и 6 - ко второму, 2, 3 и 4 - к третьему и 1 - к четвертому. Тогда на k -м шаге будем находить оптимальные маршруты перевозки груза из пунктов k -го пояса до конечного пункта. Оптимизацию будем производить с конца процесса, и потому, дойдя до k - го шага, неизвестно, в каком из пунктов k -го пояса окажется груз, перевозимый из первого пункта. Введем обозначения: k - номер шага (k = 1, 2,3,4); i - пункт, из которого осуществляются перевозки (i = 1,2,..., 9); j - пункт, в который доставляется груз (j = 2,3,.., 10); Сi,j - стоимость перевозки груза из пункта i в пункт j.
Очевидно, что минимум затрат на перевозку груза из пунктов k -го пояса до пункта 10 будет зависеть от того, в каком пункте этого пояса мы оказались. Номер i пункта, принадлежащего k -му поясу, будет являться переменной состояния системы на k -м шаге. Поскольку оптимизация осуществляется с конца процесса, то, находясь в некотором пункте i k -го пояса, принимается решение о перемещении груза в один из пунктов (k – 1)-го пояса, а направление дальнейшего движения известно из предыдущих шагов. Номер j пункта (k - 1)-го пояса будет переменной управления на k -м шаге. Для первого шага управления (k - 1) функция Беллмана представляет собой минимальные затраты на перевозку груза из пунктов 1 -го пояса в конечный пункт, т.е. F1(i) = С i,10. Для последующих шагов затраты складываются из двух слагаемых - стоимости перевозки груза Сi,j из пункта i k -го пояса в пункт j (k - 1)-го пояса и минимально возможных затрат на перевозку из пункта j до конечного пункта, т.е. - F k - 1 (i). Таким образом, функциональное уравнение Беллмана будет иметь вид
Минимум затрат достигается на некотором значении j*, которое является оптимальным направлением движения из пункта i в конечный пункт. На четвертом шаге попадаем на 4 -й пояс и состояние системы становится определенным i=1. Функция F4(1) представляет собой минимально возможные затраты по перемещению груза из 1 -го пункта в 10 -й. Оптимальный маршрут определяется в результате анализа всех шагов в обратном порядке, а выбор некоторого управления j на k -м шаге приводит к тому, что состояние системы на (k - 1)-м шаге становится определенным. Пример: решим сформулированную выше задачу, исходные данные которой приведены на рисунке. I этап. Условная оптимизация. 1-й шаг. k = 1.
На первом шаге в пункт 10 груз может быть доставлен из пунктов 7,8 или 9. Таблица 52.1
2-й шаг. k = 2. Функциональное уравнение на втором шаге принимает вид:
Все возможные перемещения груза на втором шаге и результаты расчета приведены в следующей таблице 33.2: Таблица 52.2
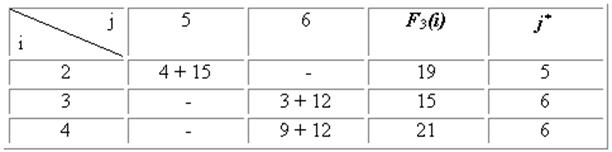
3-й шаг. k = 3.
Таблица 52.3
4-й шаг. k = 4.
Таблица 52.4
II этап. Безусловная оптимизация.
Рис. 52.2 На этапе условной оптимизации получено, что минимальные затраты на перевозку груза из пункта 1 в пункт 10 составляют F4(1) = 20. Данный результат достигается при движении груза из 1 -го пункта в 3 -й. По данным табл.33.3, из пункта 3 необходимо двигаться в пункт 6, затем - в пункт 7 (см. табл.33.2) и из него - в конечный пункт (см. табл.33.1). Таким образом, оптимальный маршрут доставки груза: 1 => 3 => 6 => 7 => 10. На рисунке он показан жирными стрелками.
Теория игр. Игровые модели. Игра – это идеализированная математическая модель коллективного поведения: несколько индивидуумов (участников, игроков) влияют на ситуацию (исход игры), причем их интересы (их выигрыши при различных возможных ситуациях) различны. Математическая теория определяет теорию игр, как раздел математики, ориентированный на построение формальных моделей принятия оптимальных решений в ситуации конкурентного взаимодействия. Данное определение главной задачей теории игр ставит последовательность действий эффективного поведения в условиях конкуренции, конфликтности.). В теории игр участников конкурирующего взаимодействия называют игроками, каждый из них имеет непустое множество допустимых действий, совершаемых им по ходу игры, которые называются ходами или выборами. Набор всех возможных ходов по одному из списка возможных ходов каждого игрока (участвующих в парах, тройках и т.д. ходов) называется стратегией. Грамотно построенные стратегии взаимно исключают друг друга, т.е. взаимно исчерпывают все способы поведения игроков. Исходом игры называется реализация игроком выбранной им стратегии. Каждому исходу игры соответствует определяемое игроками значение полезности (выигрыша), называемое платежом. Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, доступности информации и т.д. 1. В зависимости от количества игроков различают парные игры и игры n игроков. Математический аппарат реализации парных игр наиболее проработан. Игры трёх и более игроков исследовать сложнее из-за трудностей технической реализации алгоритмов решения. 2. По количеству стратегий игры бывают конечные и бесконечные. Конечной называется игра с конечным числом возможных стратегий игроков. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, то игра называется бесконечной. 3. По характеру взаимодействия игры делятся на: · бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции; · коалиционные (кооперативные) – игроки могут вступать в коалиции. В кооперативных играх коалиции жестко заданы на этапе постановки задачи и не могут меняться во время игры. 4. По характеру выигрышей игры делятся на: · игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю); · игры с ненулевой суммой. 5. По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, дуэли и др. Матричная игра – это конечная парная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям). Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования. Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.) Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные. Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. В теории математики доказано, что игры этого класса имеют решения, однако пока не разработано практически приемлемых методов их нахождения. Целью любой игры является максимизация каждым игроком своей выгоды. Смысл математической теории игр, построенной на приведенной выше классификации, состоит в формализации (упрощении) и облегчении оптимального выбора. Множество всех возможных стратегий игр составляет большое число, растущее тем сильнее, чем больше игроков и набор доступных каждому ходов. Так для пары игроков, если условия игры позволяют каждому совершить по n ходов, в игре существует 2n стратегий. Простой перебор и оценка (сравнение) такого числа стратегий представляют собой технически очень сложную задачу и неприемлемы на практике. Математический аппарат позволяет значительно снизить число требующих анализа и сравнения стратегий, отбросив заведомо неэффективные. Когда же получен ограниченный, разумный для анализа набор точек равновесия (одинаково предпочитаемых всеми игроками исходов игры), на основе анализа выигрышей игроков, выбирается наиболее рациональный результат. При выборе результата существуют два основных подхода, которые дают название окончательной стратегии игры: · Минимаксная стратегия (выбор из максимальных (наихудших) проигрышей минимальных (наилучших). · Максиминная стратегия (выбор из минимальных (наихудших) выигрышей максимальных (наилучших). Развитием теории игр с использованием методов вероятностного анализа является математическая теория принятия решений. Эта теория оперирует не действительным (актуальным) решением, а средним, которое есть ожидаемое решение игры в течение ее многократного повторения. Данное свойство актуально для решения правовых задач, поскольку нормативный характер права означает, что оно ориентировано на неопределенного субъекта и предполагает многократное повторение правоотношений. Чтобы не вдаваться в глубокие математические выкладки, отметим лишь, что теория принятия решений предлагает систему критериев (например, критерий Гурвица, Хаджи-Лемана, критерий ожидаемого значения), которые с помощью вероятностного анализа исходов игр позволяют осуществить выбор оптимального решения в условиях риска и неопределенности. Равновесие по Нэшу. В теории игр равновесием Нэша (названным в честь Джона Форбса Нэша, который предложил его) называется тип решений игры двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив своё решение в одностороннем порядке, когда другие участники не меняют решения. Такая совокупность стратегий выбранных участниками и их выигрыши называются равновесием Нэша. Из определения видно, что в ситуациях равновесия и только в них ни один игрок не заинтересован в отклонении от своей стратегии. В частности, если ситуация равновесия оказывается предметом договора между игроками, то ни один из игроков не будет заинтересован в нарушении своих обязательств. Наоборот, если в договоре зафиксирована неравновесная ситуация., то по определению найдется хотя бы один игрок, который будет заинтересован в отклонении от нее и тем самым — в нарушении этого договора. Равновесной стратегией игрока в бескоалиционной игре называется такая его стратегия, которая входит хотя бы в одну из ситуаций равновесия игры. В случае антагонистической игры равновесные стратегии игроков совпадают с их оптимальными стратегиями. Для биматричных игр, напротив, понятие оптимальной стратегии игрока нередко вообще не имеет смысла: в таких играх оптимальными оказываются не стратегии отдельных игроков, а их сочетания, (т.е. ситуации) и притом для множества всех игроков сразу. Поэтому в биматричных играх как оптимальные следует квалифицировать не действия того или иного игрока, а совокупность действий всех игроков, исход игры, ситуацию в ней. Именно в таком смысле следует понимать оптимальность приемлемых ситуаций в биматричной игре и ситуаций равновесия в ней. Значительная часть теории биматричных игр состоит в исследовании свойств их ситуаций равновесия и равновесных стратегий игроков, а также в разработка способов их нахождения. Процесс нахождения ситуаций равновесия в биматричной игре часто называется решением игры. Джорджем Нэшем было доказано существование ситуации равновесия в смешанных стратегиях для любой биматричной игры. Оптимальность по Парето. Как и в случае антагонистических игр, целью теории биматричных игр является выработка принципов оптимальности, а так же установление соответствий между свойствами игр и свойствами их решений. Чаще всего под оптимальностью подразумевают различные варианты формализованных описаний содержательных представлений о выгодности, устойчивости и справедливости. В биматричных играх могут появляться ситуации, приемлемые, (т.е. выгодные и потому устойчивые) для каждого из игроков, могут априори оказываться в том или ином смысле невыгодными (и потому не устойчивыми)для игроков. Один вариант устойчивости ситуации, отражающий черты ее выгодности, состоит в ее оптимальности по Парето. Иными словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш кого-либо из них, не уменьшив при этом выигрыш кого-либо другого. Формальное различие ситуации равновесия от ситуации, оптимальной по Парето: в первой ни один игрок, действуя в одиночку, не может увеличить своего собственного выигрыша; во второй — все игроки, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого. Вопросы об оптимальных по Парето ситуациях решаются в принципе Пример: имеются два продавца, продающие определенный товар на рынке. Оба из них знают, что чем выше цена, тем меньше общий объем продаж. Для простоты предположим, что каждый из них может продать либо 400 единиц некоторого товара, либо 100 единиц. Известно, что при продаже 800 единиц на рынке складывается цена равная 100 фунтам, при 500 единицах - 200 фунтов, а при объеме продаж 200 единиц - 500 фунтов. Матрицы выигрышей продавцов показаны в нижеследующих таблицах. Выигрыш 1 продавца.
Выигрыш 2 продавца.
Если бы игроки имели возможность и желание согласовывать свои действия, то они решили бы продать по 100 единиц и получить прибыль по 50 ООО каждый. Предположим теперь, что по каким-либо причинам они принимают решения независимо друг от друга. Каковы оптимальные стратегии для игроков в этом случае? Пара стратегий (400,100) не является ситуацией равновесия, так как в этом случае второму игроку вьгодно изменить свою стратегию на 400 и тем самым увеличить свой выигрыш с 20000 до 40000. Если рассмотреть пару стратегий (100,100), то она также не является ситуацией равновесия, поскольку каждому отдельному игроку выгодно поменять свою стратегию на 100 и получить вместо 50000 выигрыш в 80000. Если же мы рассмотрим пару стратегий (400,400), то, как легко заметить, отклонение каждого отдельного игрока является для него невыгодным. Такую ситуацию мы называем ситуацией некооперативного равновесия. Таким образом, основным определяющим свойством ситуации некооперативного равновесия является невыгодность для каждого отдельного игрока отклоняться от своей стратегии, входящей в ситуацию равновесия. В этом случае речь не идет о каких-либо договоренностях между игроками и поэтому такое равновесие называется некооперативным (равновесием по Нэшу). Напротив, когда возможность достигать определенные договоренности между игроками существует, игроки стараются найти такую пару стратегий, для которой не существует другой пары, одновременно улучшающей выигрыши обоих игроков. Такая пара стратегий называется ситуацией кооперативного (оптимальность по Парето) равновесия. Таковой является пара стратегий (100,100). 60. Игра двух лиц, в которой одним из игроков является "природа" Выбор наилучших решений в условиях неполной информации - одно из основных занятий людей. К примеру, собираясь в туристический поход, мы укладываем вещи в рюкзак с учетом неизвестной (непредсказуемой) погоды и преследуем цель получения максимума удовольствий, не превращаясь в рекордсмена по переноске тяжестей. Одним из наиболее распространенных видов управленческой деятельности также является принятие решений в условиях неполной или неточной информации, что сопряжено с неизбежным риском (и немалыми убытками) в случае принятия ошибочного решения. При принятии решений в условиях неполной информации следует различать ситуацию риска и ситуацию неопределённости. Собственно разница между риском и неопределённостью касается того, знает ли принимающий решение что-либо о вероятности наступления определённых событий. Риск присутствует тогда, когда вероятности, связанные с различными последствиями принятия решения, могут оцениваться на основе данных предшествующего периода (имеется статистическая информация о подобных ранее принимаемых решениях / о подобных изучаемой ситуациях/ т.п.). Неопределённость существует тогда, когда эти вероятности приходится определять субъективно, т.к. нет данных предшествующего периода (нет соответствующей статистики). Задача выбора решения в условиях неопределённости сводится к следующему. Пусть задан некоторый вектор S=(S1,S2,..,Sn), описывающий n состояний внешней среды, и вектор X=(X1,X2,..,Xm), описывающий m допустимых решений. Требуется найти такой вектор X*=(0,0,..,0,X i ,0,..,0), который бы обеспечивал оптимум некоторой функции полезности W(X,S) по некоторому критерию K. Значение оптимума функции W(X,S) раскрывается, исходя из постановки конкретной задачи (к примеру, если обсуждается получение прибыли, то значение функции стремятся максимизировать, если себестоимость – минимизировать). Информацию об указанной функции полезности (по сути исходные данные задачи такого типа) представляют матрицей размерности m × n c элементами Wij = F(Xi,Sj), где F - решающее правило (определяемое из постановки конкретной задачи). Следует отметить, что формирование решающего правила во многом предопределяет конечный результат расчетов (в случае его неточности даже правильный выбор критерия оптимальности и соответствующие расчеты не дают основания считать принятое решение наилучшим). При достаточно четкой экономической постановке задачи практически не возникает проблем с формированием матрицы { Wij }. Критерий принятия решения в ситуации риска. Предположим, что в нашем распоряжении имеются статистические данные, позволяющие оценить вероятность того или иного состояния внешней среды, и этот опыт может быть использован для оценки будущего. При известных вероятностях Pj для возникновения состояния Sj можно найти математическое ожидание W(X,S,P) и определить вектор X *, обеспечивающий
Глобальный и условный экстремумы
Как правило, в практических задачах необходимо определить наибольшее и наименьшее значения функции (глобальный экстремум) в некоторой области. Говорят, что функция Теорема (Вейерштрасса): если область Чтобы найти наибольшее (наименьшее) значение функции 1. Найти стационарные точки, лежащие внутри области 2. Найти наибольшее (наименьшее) значение функции на границе области 3. Сравнить полученные значения функции: самое большое (меньшее) из них будет наибольшим (наименьшим) значением функции во всей области Замечание. Если граница области определения функции состоит из нескольких частей, например, треугольник или прямоугольник, то находят наибольшее и наименьшее значения функции на каждой части, а затем сравнивают. Пример. Найти наибольшее и наименьшее значения функции Решение. 1. Найдем критические точки функции. Найденная критическая точка 2. Исследуем границу области. На участке AB: y= 1, На участке BC: На участке AC: x+y= 1, или |

 , что и целевая функция
, что и целевая функция  .
.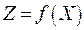 при ограничениях
при ограничениях  ,
, 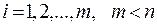 .
.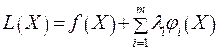 , (47.1) которая называется функцией Лагранжа. Где
, (47.1) которая называется функцией Лагранжа. Где 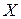 - постоянные множители Лагранжа.
- постоянные множители Лагранжа.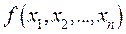 — доход, соответствующий плану
— доход, соответствующий плану 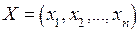 , а функция
, а функция 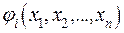 — издержки i -го ресурса, соответствующие этому плану, то
— издержки i -го ресурса, соответствующие этому плану, то 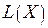 функция n + m переменных
функция n + m переменных 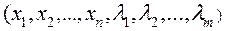 .
. (47.2)
(47.2) , т.е. в (47.1) входят уравнения связи. Таким образом, задача нахождения условного экстремума функции
, т.е. в (47.1) входят уравнения связи. Таким образом, задача нахождения условного экстремума функции 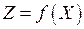 сводится к нахождению локального экстремума функции
сводится к нахождению локального экстремума функции  .
.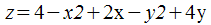 , если уравнение связи
, если уравнение связи 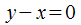 .
.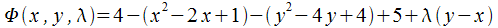 .
.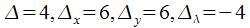 и
и 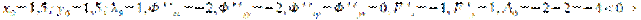 т.
т. 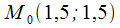 — т. условного максимума
— т. условного максимума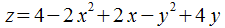 обладает условным экстремумом
обладает условным экстремумом  .
.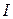 , которую он может потратить на приобретение набора товаров.
, которую он может потратить на приобретение набора товаров.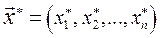 , который максимизирует его функцию полезности при заданном бюджетном ограничении.
, который максимизирует его функцию полезности при заданном бюджетном ограничении.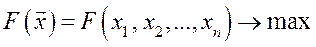
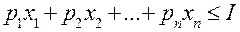 , (48.1)
, (48.1)
 , для которого
, для которого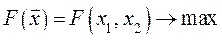
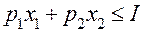 , (48.2)
, (48.2)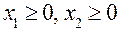 .
. Решение:
Решение: графически можно изобразить как последовательный переход на кривые безразличия более высокого уровня полезности (см. рис. 48.1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством. Из рисунка следует, что искомая точка
графически можно изобразить как последовательный переход на кривые безразличия более высокого уровня полезности (см. рис. 48.1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством. Из рисунка следует, что искомая точка 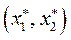 лежит на границе G, т.е. на прямой
лежит на границе G, т.е. на прямой 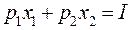 .
.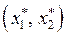 , для которой:
, для которой: 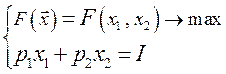 .
.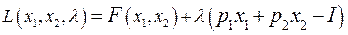 , (48.3)
, (48.3) приравняем к нулю все три частные производные этой функции, получим систему уравнений:
приравняем к нулю все три частные производные этой функции, получим систему уравнений: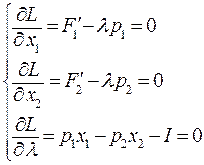 (48.4)
(48.4)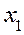 ,
, 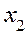 :
: 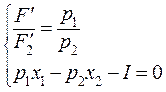 (48.5)
(48.5)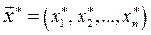 лежит на границе G и удовлетворяет условию
лежит на границе G и удовлетворяет условию 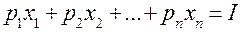 . Поэтому задача потребительского выбора формулируется аналогично в виде задачи на условный экстремум: при заданных функции
. Поэтому задача потребительского выбора формулируется аналогично в виде задачи на условный экстремум: при заданных функции 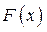 , векторе
, векторе  и величине
и величине 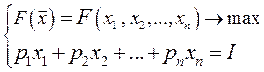 (48.6)
(48.6) (48.7)
(48.7) (48.8)
(48.8) (48.9)
(48.9)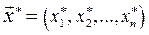 - точка условного экстремума. Это решение общей задачи потребительского выбора.
- точка условного экстремума. Это решение общей задачи потребительского выбора. называется точкой локального рыночного равновесия. Первое выражение системы (48.9) показывает, что отношение предельных полезностей продуктов в точке локального рыночного равновесия, или предельная норма замены i- го продукта j -м продуктом
называется точкой локального рыночного равновесия. Первое выражение системы (48.9) показывает, что отношение предельных полезностей продуктов в точке локального рыночного равновесия, или предельная норма замены i- го продукта j -м продуктом 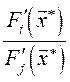 , равно отношению рыночных цен на эти продукты.
, равно отношению рыночных цен на эти продукты.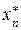 определяется функцией Беллмана:
определяется функцией Беллмана: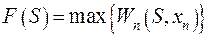 , (51.1)
, (51.1)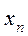 , причем
, причем  .
. ,
,  . (51.2)
. (51.2)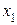 , которое этот результат доставляет. После применения этого управления система перейдет в другое состояние
, которое этот результат доставляет. После применения этого управления система перейдет в другое состояние 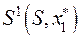 , зная которое, можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге
, зная которое, можно, пользуясь результатами условной оптимизации, найти оптимальное управление на втором шаге 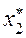 , и так далее до последнего n- го шага. Вычислительную схему динамического программирования можно строить на сетевых моделях, а также по алгоритмам прямой прогонки (от начала) и обратной прогонки (от конца к началу). Рассмотрим примеры решения различных по своей природе задач, содержание которых требует выбора переменных состояния и управления.
, и так далее до последнего n- го шага. Вычислительную схему динамического программирования можно строить на сетевых моделях, а также по алгоритмам прямой прогонки (от начала) и обратной прогонки (от конца к началу). Рассмотрим примеры решения различных по своей природе задач, содержание которых требует выбора переменных состояния и управления.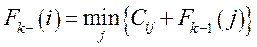 (52.1)
(52.1)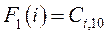




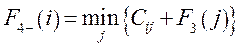


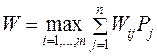 . (60.1)
. (60.1)  имеет в точке
имеет в точке 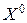 заданной области
заданной области  глобальный максимум (наибольшее значение ) или глобальный минимум (наименьшее значение), если неравенство
глобальный максимум (наибольшее значение ) или глобальный минимум (наименьшее значение), если неравенство 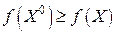 или, соответственно,
или, соответственно, 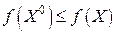 выполняется для любой точки
выполняется для любой точки 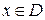 .
. в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми 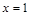 ,
, 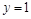 ,
,  .
.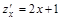
 ;
; 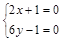
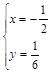 .
. не принадлежит области.
не принадлежит области. . Функция имеет вид
. Функция имеет вид  , то есть
, то есть  ;
;  при всех
при всех 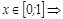 функция монотонно возрастает на этом участке, поэтому
функция монотонно возрастает на этом участке, поэтому 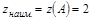 ,
, 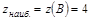 .
.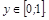 Функция имеет вид
Функция имеет вид  , то есть
, то есть 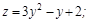
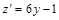 ,
,  при
при 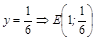 – критическая точка на участке BC.
– критическая точка на участке BC. 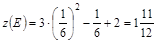 ;
; 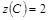 .
.
 , то есть
, то есть  ;
; 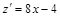 ;
;  –критическая точка на участке AC.
–критическая точка на участке AC. 


