
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о потребительском выборе.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В теории потребления предполагается, что потребитель всегда стремится максимизировать свою полезность и ограничением для него является величина дохода В общем, задача потребительского выбора (задача рационального поведения потребителя на рынке) записывается следующим образом: найти такой потребительский набор Задачу потребительского выбора (для n- мерного набора) можно записать в виде:
Задача потребительского выбора (для случая набора из двух товаров): найти такой набор
Рис. 48.1 Поиск оптимального набора Таким образом, задача потребительского выбора сводится к задаче на условный экстремум функций двух переменных: найти точку Второе уравнение выражения называется уравнением связи. Для решения задачи используем метод Лагранжа. Составим функцию Лагранжа:
где l - множитель Лагранжа. Из (48.3) следует экономический смысл множителя Лагранжа: если цены и доход меняются в одно и то же число раз l, то функция полезности и решение задачи потребительского выбора не изменятся. Для нахождения максимума функции
Исключив из этих уравнений l, получим систему двух уравнений с неизвестными Из системы находится точка Вернемся к n -мерному набору. Итак, точка
Составим функцию Лагранжа:
Для нахождения максимума функции
Исключив из уравнений множитель l, получим систему:
Решение системы Точка
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.161 (0.007 с.) |

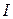 , которую он может потратить на приобретение набора товаров.
, которую он может потратить на приобретение набора товаров.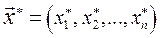 , который максимизирует его функцию полезности при заданном бюджетном ограничении.
, который максимизирует его функцию полезности при заданном бюджетном ограничении.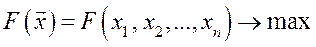
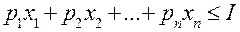 , (48.1)
, (48.1)
 , для которого
, для которого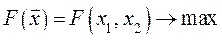
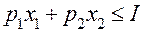 , (48.2)
, (48.2)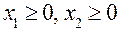 .
. Решение:
Решение: графически можно изобразить как последовательный переход на кривые безразличия более высокого уровня полезности (см. рис. 48.1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством. Из рисунка следует, что искомая точка
графически можно изобразить как последовательный переход на кривые безразличия более высокого уровня полезности (см. рис. 48.1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством. Из рисунка следует, что искомая точка 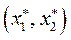 лежит на границе G, т.е. на прямой
лежит на границе G, т.е. на прямой 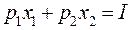 .
.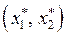 , для которой:
, для которой: 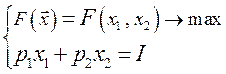 .
.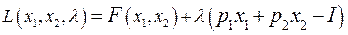 , (48.3)
, (48.3) приравняем к нулю все три частные производные этой функции, получим систему уравнений:
приравняем к нулю все три частные производные этой функции, получим систему уравнений: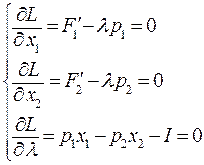 (48.4)
(48.4)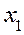 ,
, 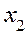 :
: 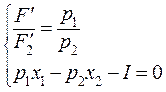 (48.5)
(48.5)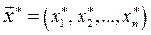 лежит на границе G и удовлетворяет условию
лежит на границе G и удовлетворяет условию 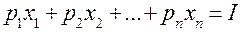 . Поэтому задача потребительского выбора формулируется аналогично в виде задачи на условный экстремум: при заданных функции
. Поэтому задача потребительского выбора формулируется аналогично в виде задачи на условный экстремум: при заданных функции 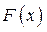 , векторе
, векторе  и величине
и величине 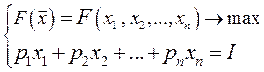 (48.6)
(48.6) (48.7)
(48.7) (48.8)
(48.8) (48.9)
(48.9)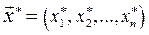 - точка условного экстремума. Это решение общей задачи потребительского выбора.
- точка условного экстремума. Это решение общей задачи потребительского выбора. называется точкой локального рыночного равновесия. Первое выражение системы (48.9) показывает, что отношение предельных полезностей продуктов в точке локального рыночного равновесия, или предельная норма замены i- го продукта j -м продуктом
называется точкой локального рыночного равновесия. Первое выражение системы (48.9) показывает, что отношение предельных полезностей продуктов в точке локального рыночного равновесия, или предельная норма замены i- го продукта j -м продуктом 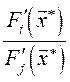 , равно отношению рыночных цен на эти продукты.
, равно отношению рыночных цен на эти продукты.


