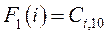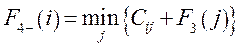Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Беллмана для оптимальных путей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математический аппарат динамического программирования, основанный на методологии пошаговой оптимизации, может быть использован при нахождении кратчайших расстояний, например, на географической карте, представленной в виде сети. Решение задачи по определению кратчайших расстояний между пунктами отправления и пунктами получения продукции по существующей транспортной сети является исходным этапом при решении таких экономических задач, как оптимальное прикрепление потребителей за поставщиками, повышение производительности транспорта за счет сокращения непроизводительного пробега и др. Пусть транспортная сеть состоит из 10 узлов, часть из которых соединены магистралями. На рисунке показана сеть дорог и стоимости перевозки единицы груза между отдельными пунктами сети, которые проставлены у соответствующих ребер. Необходимо определить маршрут доставки груза из пункта 1 в пункт 10, обеспечивающий наименьшие транспортные расходы.
Рис. 52.1 В задаче имеется ограничение - двигаться по изображенным на схеме маршрутам можно только слева на право, т.е. попав, например, в пункт 7, мы имеем право переместиться только в пункт 10 и не можем возвратиться обратно в 5 -й или 6 -й. Эта особенность транспортной сети дает право отнести каждый из десяти пунктов к одному из поясов. Будем считать, что пункт принадлежит k - му поясу, если из него попасть в конечный пункт ровно за k шагов, т.е. с заездом ровно в (k - 1)-й промежуточный пункт. Таким образом, пункты 7, 8 и 9 принадлежат к первому поясу, 5 и 6 - ко второму, 2, 3 и 4 - к третьему и 1 - к четвертому. Тогда на k -м шаге будем находить оптимальные маршруты перевозки груза из пунктов k -го пояса до конечного пункта. Оптимизацию будем производить с конца процесса, и потому, дойдя до k - го шага, неизвестно, в каком из пунктов k -го пояса окажется груз, перевозимый из первого пункта. Введем обозначения: k - номер шага (k = 1, 2,3,4); i - пункт, из которого осуществляются перевозки (i = 1,2,..., 9); j - пункт, в который доставляется груз (j = 2,3,.., 10); Сi,j - стоимость перевозки груза из пункта i в пункт j.
Очевидно, что минимум затрат на перевозку груза из пунктов k -го пояса до пункта 10 будет зависеть от того, в каком пункте этого пояса мы оказались. Номер i пункта, принадлежащего k -му поясу, будет являться переменной состояния системы на k -м шаге. Поскольку оптимизация осуществляется с конца процесса, то, находясь в некотором пункте i k -го пояса, принимается решение о перемещении груза в один из пунктов (k – 1)-го пояса, а направление дальнейшего движения известно из предыдущих шагов. Номер j пункта (k - 1)-го пояса будет переменной управления на k -м шаге.
Для первого шага управления (k - 1) функция Беллмана представляет собой минимальные затраты на перевозку груза из пунктов 1 -го пояса в конечный пункт, т.е. F1(i) = С i,10. Для последующих шагов затраты складываются из двух слагаемых - стоимости перевозки груза Сi,j из пункта i k -го пояса в пункт j (k - 1)-го пояса и минимально возможных затрат на перевозку из пункта j до конечного пункта, т.е. - F k - 1 (i). Таким образом, функциональное уравнение Беллмана будет иметь вид
Минимум затрат достигается на некотором значении j*, которое является оптимальным направлением движения из пункта i в конечный пункт. На четвертом шаге попадаем на 4 -й пояс и состояние системы становится определенным i=1. Функция F4(1) представляет собой минимально возможные затраты по перемещению груза из 1 -го пункта в 10 -й. Оптимальный маршрут определяется в результате анализа всех шагов в обратном порядке, а выбор некоторого управления j на k -м шаге приводит к тому, что состояние системы на (k - 1)-м шаге становится определенным. Пример: решим сформулированную выше задачу, исходные данные которой приведены на рисунке. I этап. Условная оптимизация. 1-й шаг. k = 1.
На первом шаге в пункт 10 груз может быть доставлен из пунктов 7,8 или 9. Таблица 52.1
2-й шаг. k = 2. Функциональное уравнение на втором шаге принимает вид:
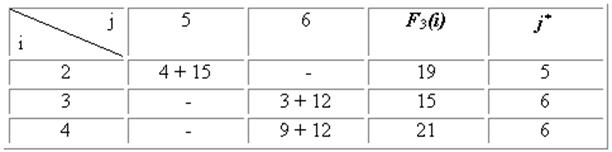
Все возможные перемещения груза на втором шаге и результаты расчета приведены в следующей таблице 33.2: Таблица 52.2
3-й шаг. k = 3.
Таблица 52.3
4-й шаг. k = 4.
Таблица 52.4
II этап. Безусловная оптимизация.
Рис. 52.2 На этапе условной оптимизации получено, что минимальные затраты на перевозку груза из пункта 1 в пункт 10 составляют F4(1) = 20. Данный результат достигается при движении груза из 1 -го пункта в 3 -й. По данным табл.33.3, из пункта 3 необходимо двигаться в пункт 6, затем - в пункт 7 (см. табл.33.2) и из него - в конечный пункт (см. табл.33.1). Таким образом, оптимальный маршрут доставки груза: 1 => 3 => 6 => 7 => 10. На рисунке он показан жирными стрелками.
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.54.147 (0.012 с.) |


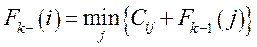 (52.1)
(52.1)