
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ оптимального решения на чувствительность в ExcelСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Проведем анализ чувствительности задачи о мебельном комбинате из лабораторной работы №2 (часть I). Для этого необходимо после запуска в Excel задачи на решениев окне "Результаты поиска решения" выделить с помощью мыши два типа отчетов: "Результаты" и "Устойчивость" (рис.3.5).
Рис.3.5. Выделение типов отчетов требуемых для анализа чувствительности
Отчет по результатам
Отчет по результатам состоит из трех таблиц (рис.3.6): 1) таблица 1 содержит информацию о ЦФ; 2) таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи; 3) таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Рис.3.6. Лист отчета по результатам Если ресурс используется полностью (то есть ресурс дефицитный), то в графе "Статус" ("Состояние") соответствующее ограничение указывается как "связанное"; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается "не связан". В графе "Значение" приведены величины использованного ресурса. Для граничных условий (строки 24, 25, 26 на рис. 3.6) в графе "Разница" показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием. Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Так, если на ресурс наложено ограничение типа Если на ресурс наложено ограничение типа
или перевести их на выпуск другой продукции. Анализ строки 23 показывает, что общее количество выпускаемых полок составляет 1220 шт., что меньше предполагаемой емкости рынка на 4080 шт. То есть запас недефицитного ресурса “Емкость рынка” может быть уменьшен до 1220 полок и это никак не повлияет на оптимальное решение (2.20). Другими словами, уменьшение спроса до 1220 полок в месяц никак не скажется на оптимальных объемах выпуска полок. На основании проведенного анализа можно сделать вывод о том, что существуют причины (ограничения), не позволяющие мебельному комбинату выпускать большее количество полок и получать большую прибыль. Проанализировать эти причины позволяет отчет поустойчивости.
Отчет по устойчивости
Отчет поустойчивости состоит из двух таблиц (рис.3.7). Таблица 1 содержит информацию, относящуюся к переменным. 1. Результат решения задачи. 2. Нормированная стоимость, которая показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи (см. рис.3.7) нормированная стоимость для полок В1 равна –20 руб./шт. (строка 5). Это означает, что если мы, несмотря на оптимальное решение (2.20), потребуем включить в план выпуска 1 полку В1, то новый план выпуска ( Коэффициенты ЦФ. 4. Предельные значения приращения целевых коэффициентов
Рис.3.7. Отчет по устойчивости для задачи о мебельном комбинате Примечание 3.1. При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может меняться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры). Таблица 2 (см. рис.3.7) содержит информацию, относящуюся к ограничениям. 1. Величина использованных ресурсов в колонке "Результ. значение". 2. Предельные значения приращения ресурсов 3. Ценность дополнительной единицы i-го ресурса (теневая цена) рассчитывается только для дефицитных ресурсов. После того как мы установили, что увеличение емкостей сушилки и склада приведет к новым планам выпуска, обеспечивающим более высокую прибыль, возникает следующий вопрос. Что выгоднее в первую очередь расширять: сушилку или склад? Ответ на этот вопрос дает графа "Теневая цена". Для емкости сушилки она равна 30 руб./шт., а для склада – 60 руб./шт. (см. рис.3.7), то есть каждая полка, которую дополнительно можно будет поместить в сушилку, увеличит прибыль на 30 руб., а каждая полка, которую дополнительно можно будет поместить на склад, увеличит прибыль на 60 руб. Отсюда вывод: в первую очередь выгодно увеличивать емкость склада готовой продукции. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 1. Что такое связывающие, несвязывающие, избыточные ограничения; дефицитные и недефицитные ресурсы? 2. Каковы предпосылки и основные задачи анализа оптимального решения на чувствительность? 3. Как графически проводится анализ изменения запаса дефицитных ресурсов? 4*. Каким образом, опираясь на результаты графического анализа, можно численно рассчитать новый (улучшенный) запас дефицитного ресурса? 5. Как графически проводится анализ изменения запаса недефицитных ресурсов? 6*. Каким образом, опираясь на результаты графического анализа, можно численно рассчитать новый запас недефицитного ресурса? 7. Что такое ценность дополнительной единицы i-го ресурса? 8. Как проводится графический анализ изменения коэффициентов ЦФ? 9*. Как численно определить диапазон изменения коэффициентов ЦФ, не изменяющий оптимального решения? 10. Какую информацию о чувствительности оптимального решения задачи ЛП можно получить из отчета по результатам и отчета по устойчивости? 11. Проанализируйте на чувствительность задачу о производстве полок (согласно своему варианту)?
4. ЛАБОРАТОРНАЯ РАБОТА №3 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. СТАНДАРТНАЯ ТРАНСПОРТНАЯ ЗАДАЧА” ЦЕЛЬ РАБОТЫ Приобретение навыков построения математических моделей стандартных транспортных задач ЛП и решения их в Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Согласно номеру своего варианта выберите условие задачи. 2. Постройте модель задачи, включая транспортную таблицу. 3. Найдите оптимальное решение задачи в Excel и продемонстрируйте его преподавателю. 4. Оформите отчет по лабораторной работе, который должен содержать: · титульный лист (см. рис.2.1); · транспортную таблицу и модель задачи с указанием всех единиц измерения; · результаты решения задачи с указанием единиц измерения.
4.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7]
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 689; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |



 , то в графе "Разница" дается количество ресурса, на которое была превышена минимально необходимая норма. Например, анализ строки 26 (см. рис. 3.6) отчета по результатам для задачи о мебельном комбинате показывает, что полок выпущено на 70 шт. больше, чем было заказано. То есть из 120 полок только 70 шт. пойдут в свободную продажу. Таким образом, можно дать следующий ответ на вопрос об изменении запаса недефицитного ресурса “Значение XB2”: обязательный заказ на производство полок В2 можно увеличить на 70 шт., то есть заказывать до 120 шт., и при этом оптимальное решение (2.20) задачи не изменится.
, то в графе "Разница" дается количество ресурса, на которое была превышена минимально необходимая норма. Например, анализ строки 26 (см. рис. 3.6) отчета по результатам для задачи о мебельном комбинате показывает, что полок выпущено на 70 шт. больше, чем было заказано. То есть из 120 полок только 70 шт. пойдут в свободную продажу. Таким образом, можно дать следующий ответ на вопрос об изменении запаса недефицитного ресурса “Значение XB2”: обязательный заказ на производство полок В2 можно увеличить на 70 шт., то есть заказывать до 120 шт., и при этом оптимальное решение (2.20) задачи не изменится.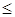 , то в графе "Разница" дается количество ресурса, которое не используется при реализации оптимального решения. Так, анализ строки 13 (см. рис. 3.6) отчета по результатам для задачи о мебельном комбинате показывает, что время столярных работ составило 4440 ч. Неизрасходованным остается 2640 ч из общего фонда времени, отведенного на столярные работы. Из этого следует, что запас недефицитного ресурса “Фонд времени по столярным работам” можно уменьшить на 2640 ч и это никак не повлияет на оптимальное решение (2.20). Отсюда следует, что количество столяров можно уменьшить на 15 человек
, то в графе "Разница" дается количество ресурса, которое не используется при реализации оптимального решения. Так, анализ строки 13 (см. рис. 3.6) отчета по результатам для задачи о мебельном комбинате показывает, что время столярных работ составило 4440 ч. Неизрасходованным остается 2640 ч из общего фонда времени, отведенного на столярные работы. Из этого следует, что запас недефицитного ресурса “Фонд времени по столярным работам” можно уменьшить на 2640 ч и это никак не повлияет на оптимальное решение (2.20). Отсюда следует, что количество столяров можно уменьшить на 15 человек
 ;
;  ;
;  ) принесет нам прибыль 106 180 руб./мес., что на 20 руб. меньше, чем в прежнем оптимальном решении.
) принесет нам прибыль 106 180 руб./мес., что на 20 руб. меньше, чем в прежнем оптимальном решении. , при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на полки В1 равно 20 руб./шт., а допустимое уменьшение – практически не ограничено (строка 5 на рис.3.7). Это означает, что если цена на полки В1 возрастет более чем на 20 руб./шт., например станет равной 61 руб./шт., то оптимальное решение изменится: станет целесообразным выпуск В1 в количестве 70 шт. А если их цена будет снижаться вплоть до нуля, то оптимальное решение (2.20) останется прежним.
, при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на полки В1 равно 20 руб./шт., а допустимое уменьшение – практически не ограничено (строка 5 на рис.3.7). Это означает, что если цена на полки В1 возрастет более чем на 20 руб./шт., например станет равной 61 руб./шт., то оптимальное решение изменится: станет целесообразным выпуск В1 в количестве 70 шт. А если их цена будет снижаться вплоть до нуля, то оптимальное решение (2.20) останется прежним.
 . В графе "Допустимое Уменьшение" показывают, на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом оптимальное решение. Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан в подразд.3.3.3.1. Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие мебельному комбинату выпускать большее, чем в оптимальном решении, количество полок и получать более высокую прибыль. В рассматриваемой задаче (вариант 0) такими ограничениями являются дефицитные ресурсы “Емкость сушилки” и “Емкость склада готовой продукции”. Поскольку знак ограничений этих запасов имеет вид
. В графе "Допустимое Уменьшение" показывают, на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом оптимальное решение. Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан в подразд.3.3.3.1. Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие мебельному комбинату выпускать большее, чем в оптимальном решении, количество полок и получать более высокую прибыль. В рассматриваемой задаче (вариант 0) такими ограничениями являются дефицитные ресурсы “Емкость сушилки” и “Емкость склада готовой продукции”. Поскольку знак ограничений этих запасов имеет вид 


