
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа №2 (часть II)Содержание книги
Поиск на нашем сайте
“АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОДНОИНДЕКСНЫХ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ” ЦЕЛЬ РАБОТЫ Приобретение навыков анализа чувствительности задач ЛП на основе различных типов отчетов, выдаваемых Microsoft Excel, о результат поиска решения. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 1. Для задачи, решенной в лабораторной работе №2 (часть I), получите в Excel все типы отчетов по результатам поиска решения, необходимые для анализа чувствительности. 2. Проанализируйте задачу на чувствительность к изменениям параметров исходной модели. 3. Результаты анализа задачи на чувствительность внесите в общий отчет по лабораторной работе №2.
3.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [5,6,7] Задачи анализа оптимального решения на чувствительность
На практике многие экономические параметры (цены на продукцию и сырье, запасы сырья, спрос на рынке, заработная плата и т.д.) с течением времени меняют свои значения. Поэтому оптимальное решение задачи ЛП, полученное для конкретной экономической ситуации, после ее изменения может оказаться непригодным или неоптимальным. В связи с этим возникает задача анализа чувствительности задачи ЛП, а именно того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение. Ограничения линейной модели классифицируются следующим образом (рис.3.1). Связывающие ограничения проходят черезоптимальную точку, например (1) и (2). Несвязывающие ограничения не проходят черезоптимальную точку, например (3), (4) и (5). Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением, – недефицитным. Ограничениеназывают избыточным в том случае, если его исключение не влияет на область допустимых решений и, следовательно, на оптимальное решение, например, (5). Выделяют следующие три задачи анализа на чувствительность. 1. Анализ сокращения или увеличения ресурсов: 1) на сколько можно увеличить (ограничения типа 2) на сколько можно уменьшить (ограничения типа 2. Увеличение (уменьшение) запаса какого из ресурсов наиболее выгодно? 3. Анализ изменения целевых коэффициентов: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?
Графический анализ оптимального решения на чувствительность
Область допустимых решений задачи на рис.3.1 – многоугольник ОABCDE. Если связывающее ограничение (дефицитный ресурс) (2) передвигать до точки F, то это приведет к расширению области допустимых решений до многоугольника ОABCFE и к получению нового оптимального решения в точке F. При этом ограничение (2) станет избыточным. Новое решение (F) лучше прежнего (C), поскольку для пересечения с точкой F линия ЦФ должна пройти по направлению вектора (выходящего из начала координат и показывающего направление максимизации ЦФ) дальше точки С (рис.3.2).
(5) (2) (4) В А С F D (1) О Е
Рис.3.1. Исходная задача ЛП для графического анализа чувствительности
(5) (2) (4) В А С F (1) О E
Рис.3.2. Анализ максимального изменения запаса дефицитного ресурса (2) с целью улучшения оптимального решения
Таким образом, чтобы графически определить максимальное изменение запаса дефицитного ресурса, улучшающее оптимальное решение, необходимо передвигать соответствующую прямую в направлении улучшения ЦФ до тех пор, пока это ограничение не станет избыточным. Графический анализ максимально возможного изменения запаса недефицитного ресурса показан на рис.3.3. Передвинем несвязывающее ограничение (3) до пересечения с оптимальным решением в точке С.
(5) (4) (2) (3) С F G (1) D О E
Рис.3.3. Анализ максимального изменения запаса недефицитного ресурса (3), не изменяющего оптимальное решение С
Это соответствует уменьшению запаса недефицитного ресурса (3), который в оптимальной точке С исходной задачи (см. рис.3.1) расходовался не полностью. Областью допустимых решений станет многоугольник OGCDE. Оптимальное решение останется прежним (точка С). Таким образом, ч тобы графически определить максимальное изменение запаса недефицитного ресурса, не меняющее оптимального решения, необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой. Для того чтобы выяснить, запас какого из дефицитных ресурсов выгоднее увеличивать в первую очередь, необходимо определить, какую пользу (например, прибыль) принесет увеличение запасов каждого из них на единицу. Для этих целей вводится понятие ценности дополнительной единицы i-го ресурса (теневая цена):
То есть сначала наращивается запас ресурса, имеющего максимальное значение Графический анализ изменения целевых коэффициентов (например, цен на производимую продукцию), не приводящих к изменению оптимального решения, проводится путем вращения линии ЦФ. При увеличении коэффициента ЦФ
или уменьшение цены 2 ( (2) (4) Н С (5)
J Увеличение
или уменьшение цены 2 ( Рис.3.4. Анализ изменения коэффициентов
Зафиксируем значение При таких поворотах точка С будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклоном прямых ограничений (1) и (2). Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной станет соответственно точка H или J. Таким образом, нижний и верхний пределы изменения цены 1 определяются значениями коэффициента
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.50 (0.006 с.) |

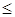 ) или уменьшить (ограничения типа
) или уменьшить (ограничения типа  ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
) запас дефицитного ресурса для улучшения оптимального значения ЦФ?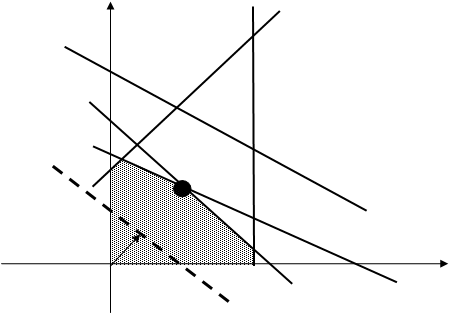 (3)
(3)
 (3)
(3)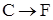
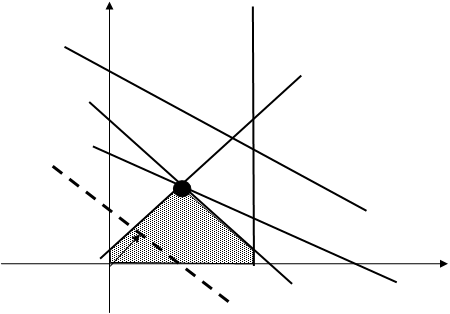
 .
.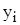 , затем – второе по величине и т.д.
, затем – второе по величине и т.д. или уменьшении коэффициента
или уменьшении коэффициента 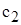 целевая прямая на графике вращается вокруг оптимальной точки по часовой стрелке. Если
целевая прямая на графике вращается вокруг оптимальной точки по часовой стрелке. Если  Уменьшение цены 1 (
Уменьшение цены 1 (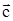 (1)
(1)


