
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Список используемых обозначенийСодержание книги
Поиск на нашем сайте СОДЕРЖАНИЕ ВВЕДЕНИЕ 5 1. ЛАБОРАТОРНАЯ РАБОТА №1 “РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel” 6 1.1. ЦЕЛЬ РАБОТЫ 6 1.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 6 1.3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП [5] 6 1.3.1. Одноиндексные задачи ЛП 7 1.3.1.1. Ввод исходных данных 7 1.3.1.2. Решение задачи 13 1.3.2. Целочисленное программирование 16 1.3.3. Двухиндексные задачи ЛП 18 1.3.4. Задачи с булевыми переменными 20 1.3.5. Возможные ошибки при вводе условий задач ЛП 22 1.4. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 22 1.5. ВАРИАНТЫ 24 2. ЛАБОРАТОРНАЯ РАБОТА №2 (ЧАСТЬ I) 27 “ОДНОИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ” 27 2.1. ЦЕЛЬ РАБОТЫ 27 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 27 2.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7] 28 2.5. ВАРИАНТЫ 38 2.4. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 40 3. ЛАБОРАТОРНАЯ РАБОТА №2 (ЧАСТЬ II) 40 “АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОДНОИНДЕКСНЫХ ЗАДАЧ 40 ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ” 40 3.1. ЦЕЛЬ РАБОТЫ 40 3.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 40 3.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [5,6,7] 41 3.3.1. Задачи анализа оптимального решения на чувствительность 41 3.3.2. Графический анализ оптимального решения на чувствительность 41 3.3.3. Анализ оптимального решения на чувствительность в Excel 44 3.3.3.1. Отчет по результатам 45 3.3.3.2. Отчет по устойчивости 47 3.4. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 48 4. ЛАБОРАТОРНАЯ РАБОТА №3 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. СТАНДАРТНАЯ ТРАНСПОРТНАЯ ЗАДАЧА” 49 4.1. ЦЕЛЬ РАБОТЫ 49 4.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 49 4.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7] 50 4.3.1. Стандартная модель транспортной задачи (ТЗ) 50 4.3.2. Пример построения модели ТЗ 52 4.4. ВАРИАНТЫ 55 4.6. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 56 5. ЛАБОРАТОРНАЯ РАБОТА №4 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ЗАДАЧА О НАЗНАЧЕНИЯХ” 57 5.1. ЦЕЛЬ РАБОТЫ 57 5.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 57 5.3. ЗАДАЧА О НАЗНАЧЕНИЯХ. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,3,6,7] 57 5.4. ПОСТАНОВКА ЗАДАЧИ О НАЗНАЧЕНИЯХ 59 5.5. РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧИ О НАЗНАЧЕНИЯХ 59 5.4. ВАРИАНТЫ 60 5.5. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 61 6. ЛАБОРАТОРНАЯ РАБОТА №5 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ОРГАНИЗАЦИЯ ОПТИМАЛЬНОЙ СИСТЕМЫ СНАБЖЕНИЯ” 61 6.1. ЦЕЛЬ РАБОТЫ 61 6.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 61 6.3. ПОСТАНОВКА ЗАДАЧИ 61 6.4. РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧИ 62 6.5. ВАРИАНТЫ 62 6.6. ЗАЩИТА РАБОТЫ 62 7. ЛАБОРАТОРНАЯ РАБОТА №6 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛП. ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПРОИЗВОДСТВЕННЫХ МОЩНОСТЕЙ” 65 7.1. ЦЕЛЬ РАБОТЫ 65 7.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 65 7.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 66 7.4. ПОСТАНОВКА ЗАДАЧИ РАСПРЕДЕЛЕНИЯ ПРОИЗВОДСТВЕННЫХ МОЩНОСТЕЙ 69 7.5. ПОСТРОЕНИЕ И РЕШЕНИЕ РЗ ЛП 70 7.6. ВАРИАНТЫ 76 7.7. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 79 ЛИТЕРАТУРА 79 ВВЕДЕНИЕ В данном учебно-методическом пособии рассмотрены основные типы задач линейного программирования, даны рекомендации по построению их математических моделей и поиску оптимальных решений средствами табличного редактора Microsoft Excel. В целях более эффективного усвоения учебного материала пособие построено по принципу лабораторных работ, разбитых по типам задач линейного программирования. В рамках лабораторной работы №1 представлены: · подробные методики и конкретные примеры решения одноиндексных и двухиндексных задач линейного программирования с различными видами ограничений; · возможные ошибки при вводе условий задач линейного программирования в MS Excel. Лабораторные работы № 2–7 содержат: · теоретическое описание математических моделей задач линейного программирования определенного типа и методики их построения; · примеры решения конкретных задач описанного типа или рекомендации к их решению. Каждая лабораторная работа включает в себя 12 вариантов учебных задач определенного типа, а также список примерных вопросов для защиты работы, охватывающих как теоретические положения, так и конкретные варианты заданий. Выбранный способ изложения учебного материала позволяет использовать данное пособие как в учебных целях, так и для решения практических задач с использованием Microsoft Excel.
СПИСОК ИСПОЛЬЗУЕМЫХ ОБОЗНАЧЕНИЙ 1) ЛП – линейное программирование. 2) ЦФ – целевая функция. 3) РЗ – распределительная задача. 4) ТЗ – транспортная задача. 5) * – вопрос повышенной сложности.
1. ЛАБОРАТОРНАЯ РАБОТА №1 “РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel” ЦЕЛЬ РАБОТЫ Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Для модели ЛП, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю. 1.3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП [5] Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи: a) создать экранную форму для ввода условия задачи: · переменных, · целевой функции (ЦФ), · ограничений, · граничных условий; b) ввести исходные данные в экранную форму: · коэффициенты ЦФ, · коэффициенты при переменных в ограничениях, · правые части ограничений; c) ввести зависимости из математической модели в экранную форму: · формулу для расчета ЦФ, · формулы для расчета значений левых частей ограничений; d) задать ЦФ (в окне "Поиск решения"): · целевую ячейку, · направление оптимизации ЦФ; e) ввести ограничения и граничные условия (в окне "Поиск решения"): · ячейки со значениями переменных, · граничные условия для допустимых значений переменных, · соотношениямежду правыми и левыми частями ограничений. 2. Решить задачу: a) установить параметры решения задачи (в окне "Поиск решения" ); b) запустить задачу на решение (в окне "Поиск решения" ); c) выбрать формат вывода решения (в окне "Результаты поиска решения"). Одноиндексные задачи ЛП Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
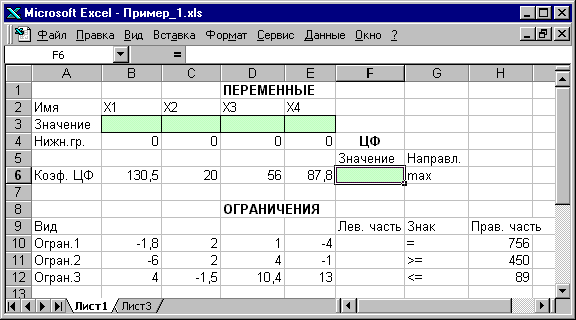
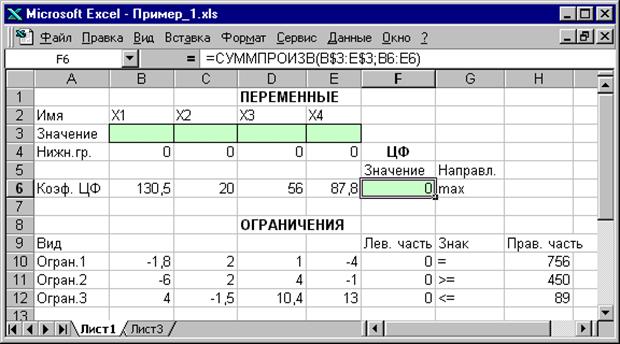
Ввод исходных данных Создание экранной формы и ввод в нее условия задачи Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.
Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке F6) В экранной форме на рис.1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 ( Ввод зависимостей из математической модели в экранную форму Зависимость для ЦФ В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter"
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится; символ: означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).
Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул (курсор в ячейке F6) Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки " · курсор в поле F6; · нажав кнопку " · выберите в окне "Категория" категорию "Математические"; · в окне "Функция" выберитефункцию СУММПРОИЗВ; · в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6 (рис.1.3); · после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Рис.1.3. Ввод формулы для расчета ЦФ в окно "Мастер функций" Зависимости для левых частей ограничений Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 – 1-е ограничение; B11, C11, D11, E11 – 2-е ограничение и B12, C12, D12, E12 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.
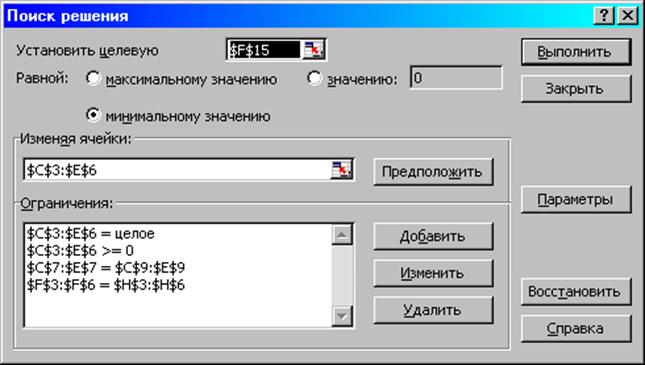
Таблица 1.1 Решение задачи Установка параметров решения задачи Задача запускается на решение в окне "Поиск решения". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (рис.1.8).
Рис.1.8. Параметры поиска решения, подходящие для большинства задач ЛП
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов). Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767. Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации. Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр "Сходимость" применяется только при решении нелинейных задач. Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применения симплекс-метода. Подтвердите установленные параметры нажатием кнопки "OK".
Запуск задачи на решение Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить". После запуска на решение задачи ЛП на экране появляется окно "Результаты поиска решения" с одним из сообщений, представленных на рис.1.9, 1.10 и 1.11.
Рис.1.9. Сообщение об успешном решении задачи
Рис.1.10. Сообщение при несовместной системе ограничений задачи
Рис.1.11. Сообщение при неограниченности ЦФ в требуемом направлении
Иногда сообщения, представленные на рис.1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5). Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра "Относительная погрешность" не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д. В окне "Результаты поиска решения" представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы". Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (рис.1.12).
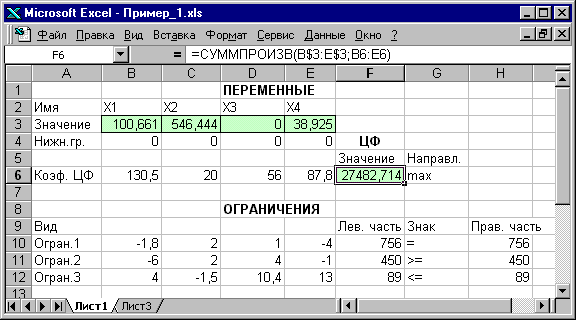
Рис.1.12. Экранная форма задачи (1.1) после получения решения
Двухиндексные задачи ЛП Двухиндексные задачи ЛП вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ. Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл.1.2).
Таблица 1.2 Исходные данные транспортной задачи
Целевая функция и ограничения данной задачи имеют вид
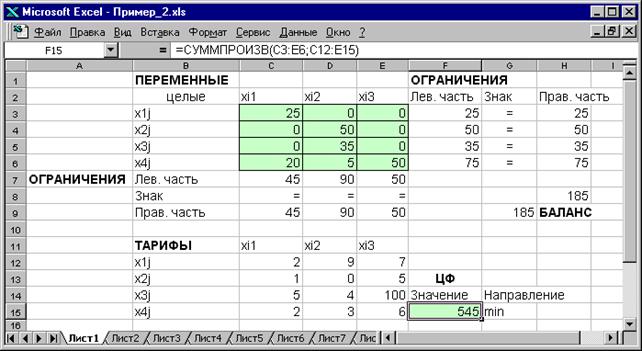
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис.1.15, 1.16, 1.17 и в табл.1.3.
Рис.1.15. Экранная форма двухиндексной задачи (1.5) (курсор в целевой ячейке F15)
Таблица 1.3 Формулы экранной формы задачи (1.5)
Рис.1.16. Ограничения и граничные условия задачи (1.5)
Рис.1.17. Экранная форма после получения решения задачи (1.5) (курсор в целевой ячейке F15)
ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 1. Каковы основные этапы решения задач ЛП в MS Excel? 2. Каков вид и способы задания формул для целевой ячейки и ячеек левых частей ограничений? 3. В чем смысл использования символа $ в формулах MS Excel? 4. В чем различие использования в формулах MS Excel символов; и:? 5. Почему при вводе формул в ячейки ЦФ и левых частей ограничений в них отображаются нулевые значения? 6. Каким образом в MS Excel задается направление оптимизации ЦФ? 7. Какие ячейки экранной формы выполняют иллюстративную функцию, а какие необходимы для решения задачи? 8. Как наглядно отобразить в экранной форме ячейки, используемые в конкретной формуле, с целью проверки ее правильности? 9. Поясните общий порядок работы с окном "Поиск решения". 10. Каким образом можно изменять, добавлять, удалять ограничения в окне "Поиск решения"? 11. Какие сообщения выдаются в MS Excel в случаях: успешного решения задачи ЛП; несовместности системы ограничений задачи; неограниченности ЦФ?
12. Объясните смысл параметров, задаваемых в окне "Параметры поиска решения". 13. Каковы особенности решения в MS Excel целочисленных задач ЛП? 14. Каковы особенности решения в MS Excel двухиндексных задач ЛП? 15. Каковы особенности решения в MS Excel задач ЛП с булевыми переменными? ВАРИАНТЫ Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл.1.5). Таблица 1.5 Варианты задач к лабораторной работе №1
Продолжение табл. 1.5
Окончание табл. 1.5
ЦЕЛЬ РАБОТЫ Приобретение навыков построения математических моделей одноиндексных задач ЛП и решения их в Microsoft Excel.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта выберите условие задачи и постройте ее модель. 2. Найдите оптимальное решение задачи в Excel и продемонстрируйте его преподавателю. Примечание 2.1. Расчет числовых данных, которые непосредственно не заданы в условии задачи, производите непосредственно в ячейках экранной формы. Например, для ввода коэффициента 3. Оформите отчет по лабораторной работе, который должен содержать: · титульный лист (рис.2.1); · исходные данные варианта; · построенную модель задачи с указанием всех единиц измерения; · результаты решения задачи.
Рис.2.1. Пример оформления титульного листа отчета по лабораторной работе 2.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7] Если в какой-либо системе (экономической, организационной, военной и т.д.) имеющихся в наличии ресурсов не хватает для эффективного выполнения каждой из намеченных работ, то возникают так называемые распределительные задачи. Цель решения распределительной задачи – отыскание оптимального распределения ресурсов по работам. Под оптимальностью распределения может пониматься, например, минимизация общих затрат, связанных с выполнением работ, или максимизация получаемого в результате общего дохода. Для решения таких задач используются методы математического программирования. Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово "программирование" заимствовано из зарубежной литературы, где оно используется в смысле "планирование". Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования. Характерные черты задач ЛП следующие: 1) показатель эффективности L представляет собой линейную функцию, заданную на элементах решения 2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. В общей форме записи модель задачи ЛП имеет вид:
Допустимое решение – это совокупность чисел Оптимальное решение – это план Для построения математической модели необходимо ответить на следующие три вопроса. 1. Что является искомыми величинами, то есть переменными этой задачи? 2. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать наилучшему, то есть оптимальному, решению? 3. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, описанные в задаче? В данной лабораторной работе рассматривается одноиндексная задача ЛП, представляющая собой общую распределительную задачу, которая характеризуется различными единицами измерения работ и ресурсов. Рассмотрим следующую задачу (вариант 0 из табл.2.1).
Постановка задачи Мебельный комбинат выпускает книжные полки А из натурального дерева со стеклом, полки B1 из полированной ДСП (древесно-стружечной плиты) без стекла и полки B2 из полированной ДСП со стеклом. Габариты полок А, B1 и В2 следующие: длина 1100 (d) мм, ширина 250 (w) мм, высота 300 (h) мм (рис.2.2). Размер листа ДСП
Рис.2.2. Габариты полок, выпускаемых мебельным комбинатом
При изготовлении полок А выполняются следующие работы: столярные, покрытие лаком, сушка, резка стекла, упаковка. Все операции, производимые в ходе столярных работ и упаковки, выполняются вручную. Полки B1 и В2 поставляются в торговую сеть в разобранном виде. За исключением операции упаковки, все остальные операции (производство комплектующих полки, резка стекла) при изготовлении полок B1 и В2, выполняются на специализированных автоматах. Трудоемкость столярных работ по выпуску одной полки А составляет 4 (Тр1) ч. Производительность автомата, покрывающего полки А лаком – 10 (Пр1) полок в час, автомата, режущего стекло – 100 (Пp2) стекол в час. Сменный фонд времени автомата для покрытия лаком – 7 (ФВ1) ч, автомата для резки стекла – 7,5 (ФВ2) ч. Сушка полок, покрытых лаком, происходит в течение суток в специальных сушилках, вмещающих 50 (V1) полок. На упаковку полки А требуется 4 (Тр2) минуты. В производстве полок заняты 40 (Р1) столяров и 14 (Р2) упаковщиков. Производительность автомата, производящего комплектующие полок B1 и В2, равна 3 (Пр3) полки в час, а его сменный фонд времени равен 7,4 (ФВ3) ч, трудоемкость упаковочных работ составляет 8 (Тр3) мин для полки В1 и 10 (Тр4) мин для полки В2. От поставщиков комбинат получает в месяц 400 (Z1) листов полированной ДСП, 230 (Z2) листов ДВП (древесно-волокнистой плиты), а также 260 (Z3) листов стекла. Из каждого листа ДВП можно выкроить 14 (К1) задних стенок полок B1 и В2, а из каждого листа стекла – 10 (К2) стекол для полок А и В2. Склад готовой продукции может разместить не более 350 (V2) полок и комплектов полок, причем ежедневно в торговую сеть вывозится в среднем 40 (N) полок и комплектов. На начало текущего месяца на складе осталось 100 (Ост) полок, произведенных ранее. Себестоимость полки А равна 205 (C1) руб., полки В без стекла – 142 (C2) руб., со стеклом – 160 (С3) руб. Маркетинговые исследования показали, что доля продаж полок обоих видов со стеклом составляет не менее 60% (Д) в общем объеме продаж, а емкость рынка полок производимого типа составляет около 5300 (V3) штук в месяц. Мебельный комбинат заключил договор на поставку заказчику 50 (З) полок типа В2 в текущем месяце. Составьте план производства полок на текущий месяц. Известны цены реализации полок: полка А – 295 (Ц1) руб., полка В без стекла – 182 (Ц2) руб., полка В со стеклом – 220 (Ц3) руб. Построение модели I этап построения модели заключается в определении (описании, задании, идентификации) переменных. В данной задаче искомыми неизвестными величинами является количество полок каждого вида, которые будут произведены в текущем месяце. Таким образом, II этап построения модели заключается в построении целевой функции, представляющей цель решения задачи. В данном случае цель – это максимизация прибыли, получаемой от продажи полок всех видов в течение месяца. Поскольку в этой задаче прибыль может быть определена как разность между ценой (Ц1, Ц2, Ц3) и себестоимостью (С1, С2, С3), то ЦФ имеет вид
III этап построения модели заключается в задании ограничений, моделирующих условия задачи. Все ограничения рассматриваемой задачи можно разделить на несколько типов. Ограничения по фонду времени (с использованием трудоемкости работ)
Левая часть ограничений по фонду времени представляет собой время, затрачиваемое на производство полок в течение месяца в количестве
Примечание 2.2. Важным моментом проверки правильности составления ограничений является проверка совпадения единиц измерения левой и правой частей ограничения. В ограничении (2.2) левая и правая части измеряются в часах, потраченных на выпуск продукции в течение месяца. Аналогично записывается ограничение (2.3) по фонду времени на упаковочные работы, в котором 14 чел. (Р2) – это количество упаковщиков:
Ограничения по фонду времени (с использованием производительности работ) Неравенство (2.4) описывает ограничение по фонду времени на покрытие лаком полок типа А. Отличие ограничений, учитывающих данные о производительности работ, от ограничений, учитывающих данные о трудоемкости работ, состоит в том, что производительность необходимо преобразовать в трудоемкость. Трудоемкость является величиной, обратной производительности. Коэффициент
Неравенство (2.5) описывает ограничение по фонду времени на резку стекла для полок типа А и В2:
Неравенство (2.6) описывает ограничение по фонду времени на производство комплектующих полок типа В1 и В2:
Ограничения по запасу расходуемых в производстве материалов (по запасу используемых для производства полок деталей)
Неравенство (2.7) описывает ограничение по запасу листов ДСП, поставляемых на комбинат ежемесячно. При этом следует учесть, что из листа ДСП надо выкраивать комплекты (верхнюю и нижнюю стороны полок, 2 боковые стороны) для производства полок. Поэтому при задании ограничения имеет смысл ориентироваться не на количество листов ДСП, а на количество комплектов для полок [правая часть (2.7)], которые можно получить из имеющегося запаса ДС
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |


 ), C3 (
), C3 ( ), D3 (
), D3 ( ), E3 (
), E3 ( ), коэффициентам ЦФ соответствуют ячейки B6 (
), коэффициентам ЦФ соответствуют ячейки B6 ( 130,5), C6 (
130,5), C6 ( 20), D6 (
20), D6 ( 56), E6 (
56), E6 (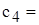 87,8), правым частям ограничений соответствуют ячейки H10 (
87,8), правым частям ограничений соответствуют ячейки H10 ( 756), H11 (
756), H11 ( 450), H12 (
450), H12 ( 89) и т.д.
89) и т.д.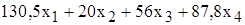 .
.
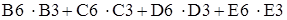 .
.
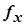 " на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
" на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом: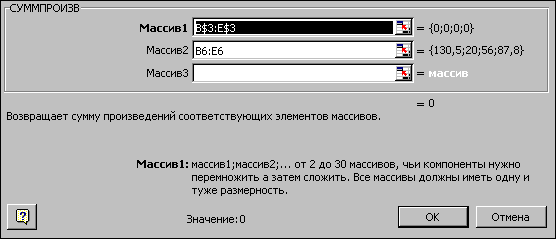




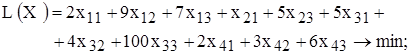


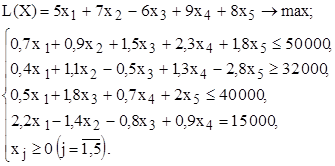
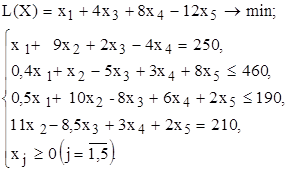


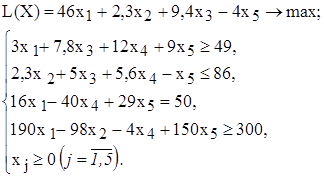
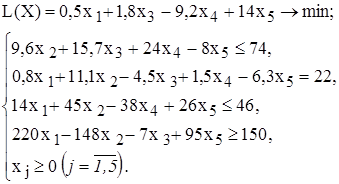
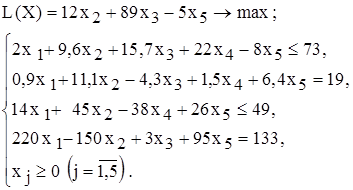

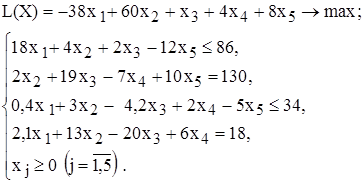

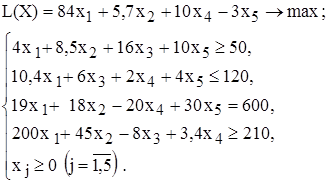

 при
при 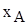 в левой части (2.3) в соответствующую ячейку надо ввести выражение =4/60, после чего в ячейке отобразится результат вычисления, то есть 0,066666667. Для ввода правой части ограничения (2.3) в соответствующую ячейку надо ввести выражение =14*8*1*22, при этом в ячейке отобразится число 2464. Этот способ позволяет четко представлять путь получения числовых данных в ячейках экранной формы, избегать ошибок при расчете параметров задачи, а также обеспечивает высокую точность расчетов.
в левой части (2.3) в соответствующую ячейку надо ввести выражение =4/60, после чего в ячейке отобразится результат вычисления, то есть 0,066666667. Для ввода правой части ограничения (2.3) в соответствующую ячейку надо ввести выражение =14*8*1*22, при этом в ячейке отобразится число 2464. Этот способ позволяет четко представлять путь получения числовых данных в ячейках экранной формы, избегать ошибок при расчете параметров задачи, а также обеспечивает высокую точность расчетов. ;
; ;
при ограничениях
;
при ограничениях

 , удовлетворяющих ограничениям задачи (2.1).
, удовлетворяющих ограничениям задачи (2.1). , при котором ЦФ принимает свое максимальное (минимальное) значение.
, при котором ЦФ принимает свое максимальное (минимальное) значение. м.
м.
 – количество полок А (шт./мес.);
– количество полок А (шт./мес.);  – количество полок В1 (шт./мес.);
– количество полок В1 (шт./мес.);  – количество полок В2 (шт./мес.).
– количество полок В2 (шт./мес.).

 – количество часов работы одного человека в течение смены; 1 см./дн. – количество смен в одном рабочем дне; 22 дн./мес. – количество рабочих дней в месяце (табл.2.1):
– количество часов работы одного человека в течение смены; 1 см./дн. – количество смен в одном рабочем дне; 22 дн./мес. – количество рабочих дней в месяце (табл.2.1):




 (
( ) при
) при 








