
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Транспортная матрица задачи без специализацииСодержание книги
Поиск на нашем сайте
Примечание 7.2. При решении ТЗ в Excel, возможно, придется увеличить относительную погрешность решения в параметрах окна "Поиск решения". Оптимальное решение ТЗ
Оптимальное решение РЗ
Значения
В данном расчете округления (до меньшего целого) обязательны, поскольку выпускаемая продукция штучная:
Определим затраты на производство продукции без специализации:
При расчете затрат на производство значения в фиктивном столбце (строке) не учитываются. Затраты, рассчитанные по формуле (7.1) и формуле (7.9), в принципе, одинаковы, но в данной задаче будут несколько различаться. Это связано с тем, что в (7.9) мы использовали уже округленные до меньшего целого значения Производство со специализацией Чтобы принять решение о том, какой корпус будем специализировать и на выпуске какой продукции, необходимо проанализировать распределение выпуска продукции по корпусам, то есть Таким образом, возникает задача оптимального распределения продукции по неспециализированным корпусам Примечание 7.3. В общем случае для ответа на вопрос, успеет ли специализируемый корпус выполнить план по конкретной продукции, необходимо использовать данные о фонде времени и производительности корпуса. Примечание 7.4. Если бы корпус Распределительная матрица задачи без специализации, в которой учтено уменьшение затрат на производство на 15%, представлена в таблице 7.4.
Таблица 7.4 Распределительная матрица задачи со специализацией
Таблица 7.5 Транспортная матрица задачи со специализацией
В результате решения задачи со специализацией получаем следующее оптимальное распределение производственных мощностей и продукции:
Общие затраты на производство со специализацией 1) затраты на производство 16 400 шт. изделий
2) затраты на производство в остальных корпусах 3) затраты на переоборудование специализируемого корпуса (матрица S в исходных данных)
Сравнивая затраты на производство заданного объема продукции без специализации Примечание 7.5. При решении подобных задач возможна ситуация, когда после проведения специализации одного из корпусов производственных мощностей других корпусов не хватает для выпуска остальной продукции (суммарный пересчитанный фонд времени меньше суммарного пересчитанного плана выпуска). Тогда вследствие специализации часть запланированного объема продукции произведена не будет, что неизбежно повлечет за собой потери прибыли от непроизведенной и непроданной продукции. Это приведет к дополнительному увеличению общих затрат.
ВАРИАНТЫ Таблица 7.6 Оптовые цены, фонды времени и план выпуска продукции
Таблица 7.7
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.1.58 (0.007 с.) |


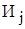
 [ч]
[ч]
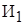


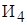





 [ч]
[ч]
 [ч] из табл.7.3 без фиктивного столбца (все значения округлены до трех знаков после запятой) имеет следующий вид:
[ч] из табл.7.3 без фиктивного столбца (все значения округлены до трех знаков после запятой) имеет следующий вид:
 [ч] получаем из оптимального решения ТЗ
[ч] получаем из оптимального решения ТЗ 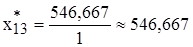 [ч];
[ч];  [ч];
[ч];  [ч];
[ч];
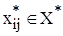 – это время, в течение которого корпус
– это время, в течение которого корпус  [шт.], воспользуемся формулой (7.7), например:
[шт.], воспользуемся формулой (7.7), например: [шт.];
[шт.];  [шт.].
[шт.].
 ;
;
 [руб].
[руб]. .
. ). Число 16 400 шт. изделий
). Число 16 400 шт. изделий  . При этом необходимо выяснить, сможет ли специализируемый корпус
. При этом необходимо выяснить, сможет ли специализируемый корпус  за свой фонд времени произвести плановое задание по выбранному виду продукции
за свой фонд времени произвести плановое задание по выбранному виду продукции 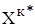 видно, что корпус успевает произвести плановые 16 400 шт. изделия
видно, что корпус успевает произвести плановые 16 400 шт. изделия  ,
,  и
и  .
.




 включают в себя:
включают в себя: [
[  ];
]; [руб.];
[руб.]; [руб.].
[руб.]. [руб.]
[руб.] [руб.] и со специализацией
[руб.] и со специализацией  [руб.], приходим к выводу, что выгодней организовать производство без специализации.
[руб.], приходим к выводу, что выгодней организовать производство без специализации. [руб./шт.]
[руб./шт.]
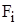 [ч]
[ч]
 [шт.]
[шт.]



