
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерии принятия решения в ситуации неопределённости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Критерий Лапласа. По принципу недостаточного основания в условиях, когда невозможно выяснить вероятности для возникновения того или иного состояния внешней среды, им сопоставляют равные вероятности, находят средний эффект для каждого из рассматриваемых вариантов решения и выбирается тот из них, где средний эффект максимален:
2. Критерий Вальда (критерий наибольшей осторожности/ пессимиста). Для каждого из рассматриваемых вариантов решения Xi выбирается самая худшая ситуация (наименьшее из Wij) и среди них отыскивается гарантированный максимальный эффект:
3. Критерий Гурвица. Ориентация на самый худший исход является своеобразной перестраховкой, однако опрометчиво выбирать и излишне оптимистичную политику. Критерий Гурвица предлагает некоторый компромисс:
где параметр 4. Критерий Сэвиджа. Суть его - нахождение минимального риска. При выборе решения по этому критерию: · матрице функции полезности (эффективности) сопоставляется новая матрица - матрица сожалений
элементы которой отражают убытки от ошибочного действия, т.е. выгоду, упущенную в результате принятия i - го решения в j - м состоянии; · по матрице D выбирается решение по пессимистическому критерию Вальда, дающее наименьшее значение максимального сожаления
Вполне логично, что различные критерии приводят к различным выводам относительно наилучшего решения. Вместе с тем возможность выбора критерия дает свободу лицам, принимающим экономические решения (если они, конечно, располагают достаточными средствами для постановки подобной задачи). Любой критерий должен согласовываться с намерениями решающего задачу и соответствовать его характеру, знаниям и убеждениям. Пример. В приморском городе решено открыть яхт-клуб. Сколько следует закупить яхт (из расчета: одна яхта на 5 человек), если предполагаемое число членов клуба колеблется от 10 до 25 человек. Годовой абонемент стоит 100 денежных единиц. Цена яхты - 170 денежных единиц. Аренда помещения и хранение яхт обходится в 730 денежных единиц в год. Решение. Несомненно, что имеет смысл рассматривать количество приобретаемых яхт в диапазоне от двух до пяти (4 варианта) и количество потенциальных яхтсменов от 10 до 25. Однако объем перебора будет великоват и потому ограничимся вариантами 10, 15, 20, 25 (если полученные выводы для смежных вариантов будут существенно разниться, проведем дополнительный, уточняющий расчет). Итак: х = {xi} = (2, 3, 4, 5) – количество яхт (i = 1,2,3,4); Для того, чтобы начать поиск решения, построим матрицу полезности, элементы которой показывают прибыль при принятии i -го решения при j –ом количестве членов яхт-клуба:
т.е. решающее правило в нашей задаче формулируется как «доход – затраты». Выполнив несложные расчеты, заполним матрицу полезности { Wij }: Таблица 60.1
Например,
Критерий принятия решения в ситуации риска. Предположим, что есть статистические данные, позволяющие оценить вероятность того или иного спроса на членство в яхт-клубе: Р = (0,1; 0,2; 0,4; 0,3). Тогда математическое ожидание величины прибыли для каждого из рассматриваемых вариантов решения (предложение яхт в яхт-клубе):
Вывод: в условиях рассматриваемой ситуации наиболее целесообразно закупить 4 яхты (в этом случае максимальная ожидаемая прибыль яхт-клуба составит 390 денежных единиц).
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 731; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.006 с.) |

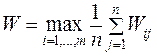 (60.2)
(60.2) (60.3)
(60.3) , (60.4)
, (60.4) принимает значение от 0 до 1 и выступает как коэффициент оптимизма. К примеру, при
принимает значение от 0 до 1 и выступает как коэффициент оптимизма. К примеру, при  (полный пессимизм) критерий Гурвица превращается в критерий Вальда, при
(полный пессимизм) критерий Гурвица превращается в критерий Вальда, при  мы расцениваем равновероятно шансы на успех и неудачу, при
мы расцениваем равновероятно шансы на успех и неудачу, при  мы более осторожны и вероятность успеха считаем меньшей (0.2), чем возможную неудачу.
мы более осторожны и вероятность успеха считаем меньшей (0.2), чем возможную неудачу.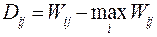 , (60.5)
, (60.5) . (60.6)
. (60.6)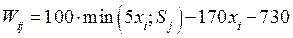 ,
,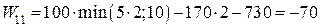

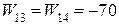 (спрос на яхты останется неудовлетворенным). Отрицательные значения показывают, что при этих соотношениях спроса на яхты и их наличия яхт-клуб несет убытки.
(спрос на яхты останется неудовлетворенным). Отрицательные значения показывают, что при этих соотношениях спроса на яхты и их наличия яхт-клуб несет убытки.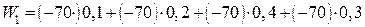 ;
;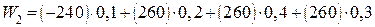 ;
; ;
;  .
.


