
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклые множества, выпуклые и вогнутые функции. Теорема Куна-Таккера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение: Функция
Определение: Функция
Если неравенства (49.1) и (49.2) считать строгими и они выполняются при Если Основные свойства выпуклых и вогнутых функций: 1. Множество точек минимума выпуклой функции, заданной на выпуклом множестве, выпукло. 2. Пусть 3. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки. 4. Если 5. Пусть функция 6. Множество точек глобальных (следовательно, и локальных) минимумов выпуклой функции Рассмотрим задачу нелинейного программирования:
при ограничениях
Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функций Говорят, что множество допустимых решений задачи (49.3) - (49.5) удовлетворяет условию регулярности, или условию Слейтера, если существует, по крайней мере, одна точка Задача (49.3) - (49.5) называется задачей выпуклого программирования, если функция Функцией Лагранжа задачи выпуклого программирования (49.3) - (49.5) называется функция:
где Точка
для всех Теорема (Куна - Таккера): Для задачи выпуклого программирования (49.3) - (49.5), множество допустимых решений которой обладает свойством регулярности,
На доп. вопрос: Что есть свойство регулярности?
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 866; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.116 (0.006 с.) |

 , заданная на выпуклом множестве
, заданная на выпуклом множестве  , называется выпуклой, если для любых двух точек
, называется выпуклой, если для любых двух точек  и
и  из
из  выполняется соотношение
выполняется соотношение (49.1)
(49.1) , заданная на выпуклом множестве
, заданная на выпуклом множестве 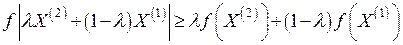 (49.2)
(49.2) является строго выпуклой (строго вогнутой). Выпуклость и вогнутость функций определяется только относительно выпуклых множеств.
является строго выпуклой (строго вогнутой). Выпуклость и вогнутость функций определяется только относительно выпуклых множеств. , где
, где  , - выпуклые (вогнутые) функции на некотором выпуклом множестве
, - выпуклые (вогнутые) функции на некотором выпуклом множестве  , то функция
, то функция  - также выпуклая (вогнутая) на
- также выпуклая (вогнутая) на  - выпуклая функция, заданная на замкнутом выпуклом множестве
- выпуклая функция, заданная на замкнутом выпуклом множестве  . Тогда локальный минимум
. Тогда локальный минимум  на
на  - выпуклая функция, заданная на выпуклом множестве
- выпуклая функция, заданная на выпуклом множестве  - точка, в которой
- точка, в которой  . Тогда в точке
. Тогда в точке  достигается локальный минимум, совпадающий с глобальным минимумом.
достигается локальный минимум, совпадающий с глобальным минимумом. , заданной на ограниченном замкнутом выпуклом множестве
, заданной на ограниченном замкнутом выпуклом множестве  является функцией-константой.
является функцией-константой. (49.3)
(49.3) , (49.4)
, (49.4) (49.5)
(49.5) и
и  , разработаны эффективные методы их решения.
, разработаны эффективные методы их решения. , принадлежащая области допустимых решений такая, что
, принадлежащая области допустимых решений такая, что  .
. является вогнутой (выпуклой), а функции
является вогнутой (выпуклой), а функции  - выпуклыми.
- выпуклыми.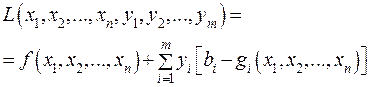 , (49.6)
, (49.6)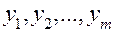 - множители Лагранжа.
- множители Лагранжа. называется седловой точкой функции Лагранжа, если
называется седловой точкой функции Лагранжа, если (49.7)
(49.7) и
и  .
. является оптимальным решением тогда и только тогда, когда существует такой вектор
является оптимальным решением тогда и только тогда, когда существует такой вектор  ,
,  , что
, что 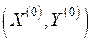 - седловая точка функции Лагранжа.
- седловая точка функции Лагранжа.


