Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Биматричные игры. Равновесие Нэша. Оптимальность Парето.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.) Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные. Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. В теории математики доказано, что игры этого класса имеют решения, однако пока не разработано практически приемлемых методов их нахождения. Рассмотрим, например, конфликтную ситуацию, в которой каждый из двух участников имеет следующие возможности для выбора своей линии поведения – игрок А может выбрать любую из стратегий A1,…,Am, игрок В может выбрать любую из стратегий B1,…,Bn. При этом всякий раз их совместный выбор оценивается вполне определенно: если игрок A выбрал i-ю стратегию А1, а игрок В — k-ю стратегию Bk, то выигрыш игрока А равен некоторому числу aik, а выигрыш игрока В некоторому, вообще говоря, другому числу bik. Иными словами, всякий раз каждый из игроков получает свой приз. Последовательно перебирая все стратегии игрока А и все стратегии игрока B мы сможем заполнить их выигрышами две таблицы
Первая из таблиц описывает выигрыши игрока А, вторая — выигрыши игрока B. Обычно эти таблицы записывают в виде матриц
Здесь А — платежная матрица игрока А, а В — платежная матрица игрока В. При выборе игроком А i-й стратегии, а игроком В — k-й стратегии их выигрыши находятся в матрицах выплат на пересечении i-x строк и k-х столбцов: в матрице А это элемент aik, а в матрице В — элемент bik. Таким образом, в случае, когда интересы игроков различны (но не обязательно противоположны), получаются две платежные матрицы: одна — матрица выплат игроку А, другая — матрица выплат игроку В. Поэтому совершенно естественно звучит название, которое обычно присваивается подобной игре, — биматричная.
Замечание, Рассматриваемые ранее матричные игры можно рассматривать, разумеется, и как биматричные, где матрица выплат игроку В противоположна матрице выплат игроку А:
или
Однако в общем случае биматричная игра — это игра с ненулевой суммой. Равновесие по Нэшу. В теории игр равновесием Нэша (названным в честь Джона Форбса Нэша, который предложил его) называется тип решений игры двух и более игроков, в котором ни один участник не может увеличить выигрыш, изменив своё решение в одностороннем порядке, когда другие участники не меняют решения. Такая совокупность стратегий выбранных участниками и их выигрыши называются равновесием Нэша. Из определения видно, что в ситуациях равновесия и только в них ни один игрок не заинтересован в отклонении от своей стратегии. В частности, если ситуация равновесия оказывается предметом договора между игроками, то ни один из игроков не будет заинтересован в нарушении своих обязательств. Наоборот, если в договоре зафиксирована неравновесная ситуация., то по определению найдется хотя бы один игрок, который будет заинтересован в отклонении от нее и тем самым — в нарушении этого договора. Равновесной стратегией игрока в бескоалиционной игре называется такая его стратегия, которая входит хотя бы в одну из ситуаций равновесия игры. В случае антагонистической игры равновесные стратегии игроков совпадают с их оптимальными стратегиями. Для биматричных игр, напротив, понятие оптимальной стратегии игрока нередко вообще не имеет смысла: в таких играх оптимальными оказываются не стратегии отдельных игроков, а их сочетания, (т.е. ситуации) и притом для множества всех игроков сразу. Поэтому в биматричных играх как оптимальные следует квалифицировать не действия того или иного игрока, а совокупность действий всех игроков, исход игры, ситуацию в ней. Именно в таком смысле следует понимать оптимальность приемлемых ситуаций в биматричной игре и ситуаций равновесия в ней.
Значительная часть теории биматричных игр состоит в исследовании свойств их ситуаций равновесия и равновесных стратегий игроков, а также в разработка способов их нахождения. Процесс нахождения ситуаций равновесия в биматричной игре часто называется решением игры. Джорджем Нэшем было доказано существование ситуации равновесия в смешанных стратегиях для любой биматричной игры. Оптимальность по Парето. Как и в случае антагонистических игр, целью теории биматричных игр является выработка принципов оптимальности, а так же установление соответствий между свойствами игр и свойствами их решений. Чаще всего под оптимальностью подразумевают различные варианты формализованных описаний содержательных представлений о выгодности, устойчивости и справедливости. В биматричных играх могут появляться ситуации, приемлемые, (т.е. выгодные и потому устойчивые) для каждого из игроков, могут априори оказываться в том или ином смысле невыгодными (и потому не устойчивыми)для игроков. Один вариант устойчивости ситуации, отражающий черты ее выгодности, состоит в ее оптимальности по Парето. Иными словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш кого-либо из них, не уменьшив при этом выигрыш кого-либо другого. Формальное различие ситуации равновесия от ситуации, оптимальной по Парето: в первой ни один игрок, действуя в одиночку, не может увеличить своего собственного выигрыша; во второй — все игроки, действуя совместно, не могут (даже нестрого) увеличить выигрыш каждого. Вопросы об оптимальных по Парето ситуациях решаются в принципе Пример: имеются два продавца, продающие определенный товар на рынке. Оба из них знают, что чем выше цена, тем меньше общий объем продаж. Для простоты предположим, что каждый из них может продать либо 400 единиц некоторого товара, либо 100 единиц. Известно, что при продаже 800 единиц на рынке складывается цена равная 100 фунтам, при 500 единицах - 200 фунтов, а при объеме продаж 200 единиц - 500 фунтов. Матрицы выигрышей продавцов показаны в нижеследующих таблицах. Выигрыш 1 продавца.
Выигрыш 2 продавца.
Если бы игроки имели возможность и желание согласовывать свои действия, то они решили бы продать по 100 единиц и получить прибыль по 50 ООО каждый. Предположим теперь, что по каким-либо причинам они принимают решения независимо друг от друга. Каковы оптимальные стратегии для игроков в этом случае? Пара стратегий (400,100) не является ситуацией равновесия, так как в этом случае второму игроку вьгодно изменить свою стратегию на 400 и тем самым увеличить свой выигрыш с 20000 до 40000. Если рассмотреть пару стратегий (100,100), то она также не является ситуацией равновесия, поскольку каждому отдельному игроку выгодно поменять свою стратегию на 100 и получить вместо 50000 выигрыш в 80000. Если же мы рассмотрим пару стратегий (400,400), то, как легко заметить, отклонение каждого отдельного игрока является для него невыгодным. Такую ситуацию мы называем ситуацией некооперативного равновесия.
Таким образом, основным определяющим свойством ситуации некооперативного равновесия является невыгодность для каждого отдельного игрока отклоняться от своей стратегии, входящей в ситуацию равновесия. В этом случае речь не идет о каких-либо договоренностях между игроками и поэтому такое равновесие называется некооперативным (равновесием по Нэшу). Напротив, когда возможность достигать определенные договоренности между игроками существует, игроки стараются найти такую пару стратегий, для которой не существует другой пары, одновременно улучшающей выигрыши обоих игроков. Такая пара стратегий называется ситуацией кооперативного (оптимальность по Парето) равновесия. Таковой является пара стратегий (100,100). 60. Игра двух лиц, в которой одним из игроков является "природа" Выбор наилучших решений в условиях неполной информации - одно из основных занятий людей. К примеру, собираясь в туристический поход, мы укладываем вещи в рюкзак с учетом неизвестной (непредсказуемой) погоды и преследуем цель получения максимума удовольствий, не превращаясь в рекордсмена по переноске тяжестей. Одним из наиболее распространенных видов управленческой деятельности также является принятие решений в условиях неполной или неточной информации, что сопряжено с неизбежным риском (и немалыми убытками) в случае принятия ошибочного решения. При принятии решений в условиях неполной информации следует различать ситуацию риска и ситуацию неопределённости. Собственно разница между риском и неопределённостью касается того, знает ли принимающий решение что-либо о вероятности наступления определённых событий. Риск присутствует тогда, когда вероятности, связанные с различными последствиями принятия решения, могут оцениваться на основе данных предшествующего периода (имеется статистическая информация о подобных ранее принимаемых решениях / о подобных изучаемой ситуациях/ т.п.). Неопределённость существует тогда, когда эти вероятности приходится определять субъективно, т.к. нет данных предшествующего периода (нет соответствующей статистики). Задача выбора решения в условиях неопределённости сводится к следующему. Пусть задан некоторый вектор S=(S1,S2,..,Sn), описывающий n состояний внешней среды, и вектор X=(X1,X2,..,Xm), описывающий m допустимых решений. Требуется найти такой вектор X*=(0,0,..,0,X i ,0,..,0), который бы обеспечивал оптимум некоторой функции полезности W(X,S) по некоторому критерию K.
Значение оптимума функции W(X,S) раскрывается, исходя из постановки конкретной задачи (к примеру, если обсуждается получение прибыли, то значение функции стремятся максимизировать, если себестоимость – минимизировать). Информацию об указанной функции полезности (по сути исходные данные задачи такого типа) представляют матрицей размерности m × n c элементами Wij = F(Xi,Sj), где F - решающее правило (определяемое из постановки конкретной задачи). Следует отметить, что формирование решающего правила во многом предопределяет конечный результат расчетов (в случае его неточности даже правильный выбор критерия оптимальности и соответствующие расчеты не дают основания считать принятое решение наилучшим). При достаточно четкой экономической постановке задачи практически не возникает проблем с формированием матрицы { Wij }. Критерий принятия решения в ситуации риска. Предположим, что в нашем распоряжении имеются статистические данные, позволяющие оценить вероятность того или иного состояния внешней среды, и этот опыт может быть использован для оценки будущего. При известных вероятностях Pj для возникновения состояния Sj можно найти математическое ожидание W(X,S,P) и определить вектор X *, обеспечивающий
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 5997; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.121.55 (0.022 с.) |
, 
.
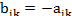
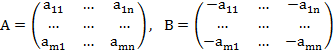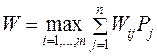. (60.1) 
