
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка задачи динамического программирования.Содержание книги
Поиск на нашем сайте
Постановку задачи динамического программирования рассмотрим на примере инвестирования, связанного с распределением средств между предприятиями. В результате управления инвестициями система последовательно переводится из начального состояния - S0 в конечное - Sn. Предположим, что управление можно разбить на n шагов и решение принимается последовательно на каждом шаге, а управление представляет собой совокупность n пошаговых управлений. На каждом шаге необходимо определить два типа переменных - переменную состояния системы Sk и переменную управления xk . Переменная Sk определяет, в каких состояниях может оказаться система на рассматриваемом k - м шаге. В зависимости от состояния S на этом шаге можно применить некоторые управления, характеризующиеся переменной xk, которые удовлетворяют определенным ограничениям и называются допустимыми. Допустим Задача динамического программирования формулируется следующим образом: требуется определить такое управление Рассмотрим более подробно особенности математической модели динамического программирования: 1. задача оптимизации формулируется как конечный многошаговый процесс управления; 2. целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага: 3. выбор управления xk на каждом шаге зависит только от состояния системы k этому шагу Sk-1, и не влияет на предшествующие шаги (нет обратной связи); 4. состояние системы Sk после каждого шага управления зависит только от предшествующего состояния системы Sk-1 и этого управляющего воздействия xh (отсутствие последействия) и может быть записано в виде уравнения состояния: Sk = fk(Sk-1 , xk), k = 1,…, n;
5. на каждом шаге управление xk зависит от конечного числа управляющих переменных, а состояние системы зависит Sk – от конечного числа параметров; 6. оптимальное управление представляет собой вектор
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.136.117 (0.009 с.) |

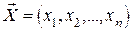 - управление, переводящее систему на состояния S0 в состояние Sn , a Sk - есть состояние системы на k -м шаге управления. Применение управляющего воздействия xk на каждом шаге переводит систему в новое состояние Sk (S, xk) и приносит некоторый результат Wk (S, xk). Для каждого возможного состояния на каждом шаге среди всех возможных управлений выбирается оптимальное управление
- управление, переводящее систему на состояния S0 в состояние Sn , a Sk - есть состояние системы на k -м шаге управления. Применение управляющего воздействия xk на каждом шаге переводит систему в новое состояние Sk (S, xk) и приносит некоторый результат Wk (S, xk). Для каждого возможного состояния на каждом шаге среди всех возможных управлений выбирается оптимальное управление  , такое, чтобы результат, который достигается за шаги с k -го по последний n - ый, оказался бы оптимальным. Числовая характеристика этого результата называется функцией Беллмана Fk (S) и зависит от номера шага k и состояния системы S.
, такое, чтобы результат, который достигается за шаги с k -го по последний n - ый, оказался бы оптимальным. Числовая характеристика этого результата называется функцией Беллмана Fk (S) и зависит от номера шага k и состояния системы S. , переводящее систему из начального состояния S0 в конечное состояние Sn, при котором целевая функция принимает наибольшее (наименьшее) значение F(S0 ,
, переводящее систему из начального состояния S0 в конечное состояние Sn, при котором целевая функция принимает наибольшее (наименьшее) значение F(S0 ,  ;
; , определяемый последовательностью оптимальных пошаговых управлений:
, определяемый последовательностью оптимальных пошаговых управлений: 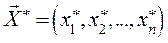 , число которых и определяет количество шагов задачи.
, число которых и определяет количество шагов задачи.


