
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приведение матричной игры к задаче линейного программирования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Игра m × n в общем случае не имеет наглядной геометрической интерпретации. Ее решение достаточно трудоемко при больших m и n, однако принципиальных трудностей не имеет, поскольку может быть сведено к решению задачи линейного программирования. Покажем это. Пусть игра m × n задана платежной матрицей p= (aij), i = 1, 2,..., m; j=1, 2,..., n. Игрок А обладает стратегиями A1, A2,..., Am, игрок В — стратегиями B 1, B2 ,..., Bm . Необходимо определить оптимальные стратегии S*A =(p*1 , p*2,..., p*m) и S*B =(q*1 , q*2,..., q*n), где p*i, q*j — вероятности применения соответствующих чистых стратегий Ai, Bj, p*1 + p*2 +...+ p*m =1, q*1 + q*2 +...+ q*n = 1. Оптимальная стратегия S*A удовлетворяет следующему требованию. Она обеспечивает игроку А средний выигрыш, не меньший, чем цена игры v, при любой стратегии игрока В и выигрыш, равный цене игры v, при оптимальной стратегии игрока B. Без ограничения общности полагаем v > 0: этого можно добиться, сделав все элементы aij ≥ 0. Если игрок А применяет смешанную стратегию S*A = (p*1 , p*2,..., p*m) против любой чистой стратегии Bj игрока В, то он получает средний выигрыш, или математическое ожидание выигрыша aj = a1j p1 + a2j p2 +...+ am j pm, j = 1, 2,..., n (т.е. элементы j -го столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий A1 , A2 ,..., Am и результаты складываются). Для оптимальной стратегии S*A все средние выигрыши не меньше цены игры v, поэтому получаем систему неравенств:
Каждое из неравенств можно разделить на число v > 0. Введем новые переменные:
Тогда система (40.1) примет вид:
Цель игрока А — максимизировать свой гарантированный выигрыш, т.е. цену игры v. Разделив на v ≠ 0 равенство p1 + p2 +...+ pm = 1, получаем, что переменные xi (i = 1, 2,..., m) удовлетворяют условию: x1 + x2 +...+ xm = 1/v. Максимизация цены игры v эквивалентна минимизации величины 1/v. Поэтому задача может быть сформулирована следующим образом: определить значения переменных xi ≥ 0, i = 1, 2,..., m так, чтобы они удовлетворяли линейным ограничениям (58.3) и при этом линейная функция
обращалась в минимум. Это задача линейного программирования. Решая задачу (58.3)—(58.4), получаем оптимальное решение p*1 + p*2 +...+ p*m и оптимальную стратегию SA. Для определения оптимальной стратегии S*B = (q*1 + q*2 +...+ q*n) следует учесть, что игрок В стремится минимизировать гарантированный выигрыш, т.е. найти
которые следуют из того, что средний проигрыш игрока В не превосходит цены игры, какую бы чистую стратегию не применял игрок А.
то получим систему неравенств:
Переменные yj (1, 2,..., n) удовлетворяют условию y1 + y2 +...+ yn = 1/v. Игра свелась к следующей задаче: определить значения переменных yj ≥ 0, j = 1, 2,..., n, которые удовлетворяют системе неравенств (58.7) и максимизируют линейную функцию
Решение задачи линейного программирования (58.6), (58.7) определяет оптимальную стратегию S*B = (q*1 + q*2 +...+ q*n). При этом цена игры
Составив расширенные матрицы для задач (58.3), (58.4) и (58.7), (58.8), убеждаемся, что одна матрица получилась из другой транспонированием:
Таким образом, задачи линейного программирования (58.3), (58.4) и (58.7), (58.8) являются взаимно-двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно-двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности. Приведем примеры экономических задач, которые описываются игровыми моделями m × n и могут быть решены методами линейного программирования. При решении произвольной конечной игры размера m × n рекомендуется придерживаться следующей схемы: 1. Исключить из платежной матрицы заведомо невыгодные стратегии по сравнению с другими стратегиями. Такими стратегиями для игрока А (игрока В) являются те, которым соответствуют строки (столбцы) с элементами, заведомо меньшими (большими) по сравнению с элементами других строк (столбцов). 2. Определить верхнюю и нижнюю цены игры и проверить, имеет ли игра седловую точку. Если седловая точка есть, то соответствующие ей стратегии игроков будут оптимальными, а цена совпадает с верхней (нижней) ценой. 3. Если седловая точка отсутствует, то решение следует искать в смешанных стратегиях. Для игр размера m × n рекомендуется симплексный метод, для игр размера 2×2, 2×n, n×2 возможно геометрическое решение. На практике реализация оптимального решения Другой путь — при многократном повторении игры — в каждой партии чистые стратегии применяются в виде случайной последовательности, причем каждая из них — с частотой, равной ее вероятности в оптимальном решении. Рассмотрим экономическую задачу, сводящуюся к игровой модели. Пример: предприятие выпускает скоропортящуюся продукцию, которую может сразу отправить потребителю (стратегия A 1), отправить на склад для хранения (стратегия A 2) или подвергнуть дополнительной обработке (стратегия A 3) для длительного хранения. Потребитель может приобрести продукцию: немедленно (стратегия B 1), в течение небольшого времени (B 2), после длительного периода времени (B 3). В случае стратегий A 2 и A 3, предприятие несет дополнительные затраты на хранение и обработку продукции, которые не требуются для A 1, однако при A 2 следует учесть возможные убытки из-за порчи продукции, если потребитель выберет стратегии B 2 или B 3. Определить оптимальные пропорции продукции для применения стратегий A 1, A 2, A 3 руководствуясь "минимаксным критерием" (гарантированный средний уровень убытка) при матрице затрат, представленной таблице.
Решение: Получаем игру с платежной матрицей Игра упростилась: По формулам находим: Вывод: оптимальная стратегия производителя продукции
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 728; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.007 с.) |

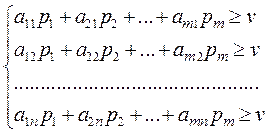 (58.1)
(58.1) (58.2)
(58.2)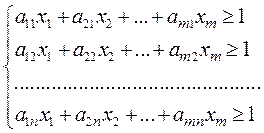 (58.3)
(58.3) (58.4)
(58.4) . Переменные q1 , q2,..., qn удовлетворяют неравенствам:
. Переменные q1 , q2,..., qn удовлетворяют неравенствам: , (58.5)
, (58.5) , (58.6)
, (58.6) . (58.7)
. (58.7) (58.8)
(58.8) (58.9)
(58.9)
 в смешанных стратегиях может происходить несколькими путями. Первый состоит в физическом смешении чистых стратегий Ai - в пропорциях, заданных вероятностями pi.
в смешанных стратегиях может происходить несколькими путями. Первый состоит в физическом смешении чистых стратегий Ai - в пропорциях, заданных вероятностями pi.
 . В этой матрице первую строку можно отбросить как невыгодную (ее элементы меньше соответствующих элементов второй строки). Матрица примет вид
. В этой матрице первую строку можно отбросить как невыгодную (ее элементы меньше соответствующих элементов второй строки). Матрица примет вид  . Элементы первого столбца больше соответствующих элементов второго столбца, поэтому его можно отбросить.
. Элементы первого столбца больше соответствующих элементов второго столбца, поэтому его можно отбросить. .
. ,
,  ,
, 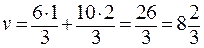 .
. , т.е. стратегия A 1 не применяется, 1/3 продукции отправляется на склад (стратегия A 2), 2/3 продукции дополнительно обрабатывается (стратегия A 3), при этом цена игры
, т.е. стратегия A 1 не применяется, 1/3 продукции отправляется на склад (стратегия A 2), 2/3 продукции дополнительно обрабатывается (стратегия A 3), при этом цена игры  .
.


