
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Понятие линейного программирования. Виды задач линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными. Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ. Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач. В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса: · задачи линейного программирования, · задачи нелинейного программирования. Если целевая функция и функции ограничений – линейные функции, то соответствующая задача поиска экстремума является задачей линейного программирования. Если хотя бы одна из указанных функций нелинейна, то соответствующая задача поиска экстремума является задачей нелинейного программирования. Глава 1. Понятие линейного программирования. Виды задач линейного программирования Линейное программирование (ЛП) – один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого и начала развиваться сама дисциплина " математическое программирование ". Термин "программирование" в названии дисциплины ничего общего с термином "программирование (т.е. составление программы) для ЭВМ" не имеет, т.к. дисциплина " линейное программирование " возникла еще до того времени, когда ЭВМ стали широко применяться для решения математических, инженерных, экономических и др. задач.
Термин " линейное программирование " возник в результате неточного перевода английского " linear programming ". Одно из значений слова "programming" - составление планов, планирование. Следовательно, правильным переводом английского " linear programming " было бы не " линейное программирование ", а "линейное планирование", что более точно отражает содержание дисциплины. Однако, термины линейное программирование, нелинейное программирование, математическое программирование и т.д. в нашей литературе стали общепринятыми и поэтому будут сохранены. Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности. Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира. Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д. Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
Постановка задач линейного программирования и исследование их структуры Большинство задач, решаемых методами исследования операций, может быть сформулировано так:максимизировать F(x1, x2,., xn) при ограничениях:
где f(x1, x2,., xn) - целевая функция, или критерий эффективности (например, прибыль от производства каких-либо видов продукции, стоимость перевозок и т.п.); X={x1,.,xn} - варьируемые параметры; g1(x),.,gm(x) - функции, которые задают ограничения на имеющиеся ресурсы. В рассматриваемом случае все ограничения имеют вид неравенств. Иногда они могут быть смешанными, то есть неравенства и равенства. Если все ограничения задачи ЛП имеют вид строгих равенств то данная форма записи называется канонической.
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие. Задача 1. Пример решения задач линейного программирования симплекс–методом.
Решение. Приводим задачу к каноническому виду. Для этого в левую часть правого ограничения вводим дополнительные переменные Х4, Х5 и Х6 с коэффициентом +1. В целевую функцию переменные Х4, Х5 и Х6 входят с коэффициентом 0. Получим:
Находим начальное опорное решение. Для этого свободные переменные приравниваем к 0.
Получаем опорное решение.
С единичным базисом Б1.
Вычисляем оценки разложения векторов условий по базису опорного решения по формуле.
Сб = (с1, с2,..., сm) — вектор коэффициентов целевой функции при базисных переменных Xk = (x1k, x2k,..., xmk) — вектор разложения соответствующего вектора Аk по базису опорного решения Сk — коэффициент целевой функции при переменной хk.
Оценки векторов входящих в базис всегда равны нулю. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу: Таблица 1
Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце "Б" записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов соответствует номерам разрешенных неизвестных в уравнениях ограничениях. Во втором столбце таблицы "Сб" записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце "Сб" оценки единичных векторов, входящих в базис, всегда равных нулю. В последней строке таблицы с оценками Δk в столбце "А0" записываются значения целевой функции на опорном решении Z(X1). Начальное опорное решение не является оптимальным, так как в задаче на максимум оценки Δ1 = -47, Δ2= -39, Δ3= -36 для векторов А1, А2 и А3 отрицательные. По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше. Определим, введение какого из двух векторов приведет к большему приращению целевой функции. Приращение функции находится по формуле: Вычислим значение D по формуле: Полученные значения записываем в таблицу. Находим приращение целевой функции при введении в базис первого вектора Следовательно, для более быстрого приближения к оптимальному решению необходимо ввести в базис опорного решения вектор А1 вместо первого вектора базиса А6, так как минимум параметра D01 достигается в третьей строке. Производим преобразование Жордана с элементом Х31 =396, получаем второе опорное решение Х2 = (2.3;0;0;43.2;288.2;0) с базисом Б2 = (А4, А5, А1).
Таблица 2
Это решение является единственным оптимальным, так как для всех векторов, не входящих в базис оценки положительные Δ2 = 15.05, Δ3 = 19.46, Δ6 = 0.1175. Ответ: max f(X)=108.1 при Х= (2.3;0;0;43.2;288.2;0) Формализация 1. Шаг 1. Задаются начальные границы отрезка 2. Шаг 2. Рассчитывают начальные точки деления:
и значения в них целевой функции:
Если Иначе 3. Шаг 3. Если Иначе возврат к шагу 2. Шаг 3. Если Иначе возврат к шагу 2 Задача 2. Пример решения задач нелинейного программирования методом Фибоначчи. Найти min функции f(x)=18 Решение: Fn+1 = F10 = 55; Fn+1 = F9 = 34; Fn = F8 = 21; Fn-1 = F7 = 13; Fn-2 = F6 = 8; Fn-3 = F5 = 5; Fn-4 = F4 = 3; Fn-5 = F3 = 2; Fn-6 = F2 = 1; Fn-7 = F1 = 1; Итерация 1. Х11 = а + X21 = a+ f (x11)=18x2 - 20x - 32= 18 ∙(15,2)2 – 20∙ (15,2) - 32 = 4158,72 - 304 - 32 = 3822,72 f(x21)= 18x2 - 20x – 32=18∙(24,72)2 – 20∙(24,72) - 32 = 10998 - 494,4 - 32=10471,6 f(x11) < f(x21), следовательно отрезок ограничен [ 0; 24,72 ]. Итерация 2. x12 = a + x22 = a + f(x12) = 18x2 - 20x – 32 = 18 ∙ (9,4)2 – 20 ∙ (9,4) – 32 = 1590,48 – 188 - 32 = 1370,48 f(x22)= 18x2 - 20x – 32 = 18 ∙ (15,3)2 – 20 ∙ (15,3) – 32 = 4213,62 – 306 – 32 = 3875,62 f(x12 ) < f(x22 ), следовательно отрезок ограничен [ 0; 15,3 ]. Итерация 3. x13= a + x23= a + f(x13) = 18x2 - 20x – 32 = 18 ∙ (5,8)2 – 20 ∙ (5,8) – 32 = 605,52 – 116 – 32 = 457,52 f(x23) = 18x2 - 20x – 32 = 18 ∙ (9,5)2 – 20 ∙ (9,5) – 32 = 1624,5 – 190 – 32 = 1402,5 f(x13) < f(x23), следовательно отрезок ограничен [ 0; 9,5 ]. Итерация 4. x14 = a + x24 = a + f(x14) = 18x2 - 20x – 32 = 18 ∙ (3,61)2 – 20 ∙ (3,61) – 32 = 234 – 72,2 – 32 = 129,8 f(x24) = 18x2 - 20x – 32 = 18 ∙ (5,8)2 – 20 ∙ (5,8) – 32 = 605,52 – 116 – 32 = 457,52 f(x14) < f(x24), следовательно отрезок ограничен [ 0; 5,8 ]. Итерация 5. x15 = a + x25 = a + f(x15) = 18x2 - 20x – 32 = 18 ∙ (2,18)2 – 20 ∙ (2,18) – 32 = 85,5 – 43,6 – 32 = 9,9 f(x25) = 18x2 - 20x – 32 = 18 ∙ (3,63)2 – 20 ∙ (3,63) – 32 = 237,06 – 72,6 – 32 = 132,46 f(x15) < f(x25), следовательно отрезок ограничен [ 0; 3,63 ].
Итерация 6. x16 = a + x26 = a +
f(x16) = 18x2 - 20x – 32 = 18 ∙ (1,5)2 – 20 ∙ (1,5) – 32 = 40,5 – 30 – 32 = -21,5 f(x26) = 18x2 - 20x – 32 = 18 ∙ (2,2)2 – 20 ∙ (2,2) – 32 = 87,12 – 44 – 32 = 11,12 f(x16) < f(x26), следовательно отрезок ограничен [ 0; 2,2 ]. Итерация 7. x17 = a + x27 = a + f(x17) = 18x2 - 20x – 32 = 18 ∙ (0,726)2 – 20 ∙ (0,726) – 32 = 9,486 – 14,52 – 32 = -37,034 f(x27) = 18x2 - 20x – 32 = 18 ∙ (1,47)2 – 20 ∙ (1,47) – 32 = 38,88 – 29,4 – 32 = -22,52 f(x17) < f(x27), следовательно отрезок ограничен [ 0; 1,47 ]. Итерация 8. x18 = a + X28 = a + f(x18) = 18x2 - 20x – 32 = 18 ∙ (0,735)2 – 20 ∙ (0,735) – 32 = 9,72 – 14,7 – 32 = -36,98 f(x28) = 18x2 - 20x – 32 = 18 ∙ (0,735)2 – 20 ∙ (0,735) – 32 = 9,72 – 14,7 – 32 = -36,98 f(x18) = f(x28) = -36,98 – точка min функции. Ответ: min f(x)= -36,98 Заключение Математическое моделирование как инструмент познания завоевывает все новые и новые позиции в различных областях деятельности человека. Оно становится главенствующим направлением в проектировании и исследовании новых систем, анализе свойств существующих систем, выборе и обосновании оптимальных условий их функционирования и т.п. Изучение математического моделирования открывает широкие возможности для осознания связи информатики с математикой и другими науками. Абстрактное моделирование с помощью компьютеров – вербальное, информационное, математическое – в наши дни стало одной из информационных технологий в познавательном плане исключительно мощной. Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многообразны и сложны, что лучшим способом изучения часто является построение модели, отражающей лишь какую – то часть реальности.
Список использованной литературы 1. Замков О.О., Толстопятенко А.В., Черешных Ю.Н. Математические методы в экономике: Учебник. - М.: МГУ им. М.В.Ломоносова, Издательство «ДИС», 1997. 2. Конспект лекций по предмету «Основы математического моделирования социально-экономических процессов». 3. Минюк С.А. Математические методы и модели в экономике: Учеб. пособие / Минюк С.А., Ровба Е.А., Кузьмич К.К. - Мн.: ТетраСистемс, 2002. 4. Смородинский С.С., Батин Н. В. Оптимизация решений на основе методов и моделей математического программирования. Мн.: БГУИР, 2003. 5. Экономико-математические методы и модели/ Под. ред. А. В. Кузнецова. Мн.: БГЭУ.1999.
Введение Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными. Для решения задач математического программирования разработаны и разрабатываются специальные методы и теории. Так как при решении этих задач приходится выполнять значительный объем вычислений, то при сравнительной оценке методов большое значение придается эффективности и удобству их реализации на ЭВМ.
Математическое программирование можно рассматривать как совокупность самостоятельных разделов, занимающихся изучением и разработкой методов решения определенных классов задач. В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса: · задачи линейного программирования, · задачи нелинейного программирования. Если целевая функция и функции ограничений – линейные функции, то соответствующая задача поиска экстремума является задачей линейного программирования. Если хотя бы одна из указанных функций нелинейна, то соответствующая задача поиска экстремума является задачей нелинейного программирования. Глава 1. Понятие линейного программирования. Виды задач линейного программирования Линейное программирование (ЛП) – один из первых и наиболее подробно изученных разделов математического программирования. Именно линейное программирование явилось тем разделом, с которого и начала развиваться сама дисциплина " математическое программирование ". Термин "программирование" в названии дисциплины ничего общего с термином "программирование (т.е. составление программы) для ЭВМ" не имеет, т.к. дисциплина " линейное программирование " возникла еще до того времени, когда ЭВМ стали широко применяться для решения математических, инженерных, экономических и др. задач. Термин " линейное программирование " возник в результате неточного перевода английского " linear programming ". Одно из значений слова "programming" - составление планов, планирование. Следовательно, правильным переводом английского " linear programming " было бы не " линейное программирование ", а "линейное планирование", что более точно отражает содержание дисциплины. Однако, термины линейное программирование, нелинейное программирование, математическое программирование и т.д. в нашей литературе стали общепринятыми и поэтому будут сохранены. Итак, линейное программирование возникло после второй мировой войны и стало быстро развиваться, привлекая внимание математиков, экономистов и инженеров благодаря возможности широкого практического применения, а также математической стройности. Можно сказать, что линейное программирование применимо для решения математических моделей тех процессов и систем, в основу которых может быть положена гипотеза линейного представления реального мира. Линейное программирование применяется при решении экономических задач, в таких задачах как управление и планирование производства; в задачах определения оптимального размещения оборудования на морских судах, в цехах; в задачах определения оптимального плана перевозок груза (транспортная задача); в задачах оптимального распределения кадров и т.д. Задача линейного программирования (ЛП), как уже ясно из сказанного выше, состоит в нахождении минимума (или максимума) линейной функции при линейных ограничениях.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.29 (0.009 с.) |

 (1.1.1)
(1.1.1)







 :
: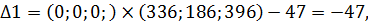















 и точность
и точность  .
. (2.1.4)
(2.1.4) (2.1.5)
(2.1.5) (2.1.6)
(2.1.6) (2.1.7)
(2.1.7) (для поиска max изменить неравенство на
(для поиска max изменить неравенство на  ), то
), то 
 .
. , то
, то  и останавливаемся.
и останавливаемся. , то
, то  и останавливаемся.
и останавливаемся.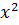 – 20х – 32 на отрезке [ 0; 40 ] за 8 шагов.
– 20х – 32 на отрезке [ 0; 40 ] за 8 шагов. ∙(b - a) = a +
∙(b - a) = a +  ∙(b – a) =
∙(b – a) =  ∙ 40 = 15,2
∙ 40 = 15,2 ∙(b – a) = a +
∙(b – a) = a +  ∙(b – a) =
∙(b – a) =  ∙ 40 = 24,72
∙ 40 = 24,72 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 24,72 = 9,4
∙ 24,72 = 9,4 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 24,72 = 15,4
∙ 24,72 = 15,4 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) = 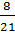 ∙ 15,3 = 5,8
∙ 15,3 = 5,8 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 15,3 = 9,5
∙ 15,3 = 9,5 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 9,5 = 3,61
∙ 9,5 = 3,61 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 9,5 = 5,8
∙ 9,5 = 5,8 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 5,8 = 2,18
∙ 5,8 = 2,18 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 5,8 = 3,63
∙ 5,8 = 3,63 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 3,63 = 1,5
∙ 3,63 = 1,5 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 3,63 = 2,2
∙ 3,63 = 2,2 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 2,2 = 0,726
∙ 2,2 = 0,726 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 2,2 = 1,47
∙ 2,2 = 1,47 ∙ (b – a) = a +
∙ (b – a) = a + 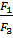 ∙ (b – a) =
∙ (b – a) =  ∙ 1,47 = 0,735
∙ 1,47 = 0,735 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) = 


