
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи о назначениях и о коммивояжере как частные случаи целочисленных злп.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При решении многих задач нецелочисленное решение не имеет смысла. Раздел математического программирования, в котором на экстремальные задачи налагается условие дискретности переменных при конечной области допустимых решений, называется дискретным программированием. При наличии условия целочисленности имеется в виду подраздел дискретного программирования - целочисленное программирование. В экономике много задач с физической неделимостью объектов, предметов и факторов расчета. К примеру, нельзя построить 1,7 здания, 6,1 завода, 1,07 автомобиля, произвести 1,7 замера, осуществить 3,4 путешествия, купить 4,5 туристических путевок. Задача о назначении: имеет n исполнителей, которые могут выполнять n различных работ. Известна полезность Математическая модель задачи примет вид:
Каждый исполнитель назначается только на одну работу:
На каждую работу назначается только один исполнитель:
Условия неотрицательности и целочисленности:
Задача коммивояжера: коммивояжер должен посетить один, и только один, раз каждый из n городов и вернуться в исходный пункт. Его маршрут должен минимизировать суммарную длину пройденного пути. Математическая модель задачи:
Условия неотрицательности и целочисленности
Добавляется условие прохождение маршрута через все города, т.е. так называемое условие цикличности. Иначе, маршрут должен представлять собой замкнутую ломаную, без пересечений в городах-точках.
Определение: экстремальная задача линейного программирования, в которой на решение налагается целочисленность компонент, является задачей целочисленного программирования и называется целочисленной задачей.
Определение: экстремальная задача линейного программирования, в которой на решение налагается целочисленность нескольких компонент, является задачей целочисленного программирования и называется частично целочисленной задачей.
Метод ветвей и границ.
Пусть
Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи. Если среди компонент плана имеются дробные числа, то необходимо осуществить переход к новым планам, пока не будет найдено решение задачи. Метод ветвей и границ основан на предположении, что наш оптимальный нецелочисленный план дает значение функции, большее, чем всякий последующий план перехода. Пусть переменная 1. либо меньше или равно ближайшему меньшему целому числу 2. либо больше или равно ближайшему большему целому числу Определяя эти числа, находим симплексным методом решение двух задач:линейного программирования:
и
Возможны четыре случая при решении этой пары задач: 1. Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции дают решение исходной задачи. 2. Одна из задач неразрешима, а другая имеет нецелочисленный оптимальный план. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу и строим две задачи, аналогичные предыдущим. 3. Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции от планов и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и дает искомое решение. 4. Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда рассматриваем ту из задач, для которой значение целевой функции является наибольшим. И строим две задачи. Алгоритм метода ветвей и границ: 1. Находим решение задачи линейного программирования без учета целочисленности. 2. Составляет дополнительные ограничения на дробную компоненту плана. 3. Находим решение двух задач с ограничениями на компоненту. 4. Строим в случае необходимости дополнительные ограничения, согласно возможным четырем случаям получаем оптимальный целочисленный план либо устанавливаем неразрешимость задачи.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 694; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.213.36 (0.006 с.) |

 , связанная с выполнением i-м исполнителем j-й работы
, связанная с выполнением i-м исполнителем j-й работы  ,
,  . Необходимо назначить исполнителей на работы так, чтобы добиться максимальной полезности, при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой должнен быть закреплен только один исполнитель.
. Необходимо назначить исполнителей на работы так, чтобы добиться максимальной полезности, при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой должнен быть закреплен только один исполнитель. (42.1)
(42.1) (42.2)
(42.2) (42.3)
(42.3) ,
,  ,
,  ,
, 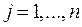 . (42.4)
. (42.4)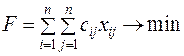 (42.5)
(42.5) (42.7)
(42.7)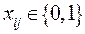 ,
,  . (42.8)
. (42.8) (43.1)
(43.1) ,
,  , (43.2)
, (43.2) ,
,  - целые,
- целые,  . (43.3)
. (43.3) в плане – дробное число. Тогда в оптимальном плане ее значение будет, по крайней мере:
в плане – дробное число. Тогда в оптимальном плане ее значение будет, по крайней мере: ;
; .
. (43.4)
(43.4) (43.6)
(43.6) ,
,  - целые,
- целые,  . (43.7)
. (43.7) , (43.9)
, (43.9) (43.10)
(43.10) - целые,
- целые, 


