
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о существовании оптимального решения.Содержание книги
Поиск на нашем сайте
Пусть одним из методов решения транспортной задачи найден опорный план, содержащий m+n - 1 занятых клеток (в некоторых из них могут стоять нули). Поставим в соответствие каждому пункту отправления Аi некоторое число Эти числа назовем потенциалами, соответственно, пунктов отправления и пунктов назначения. Вопрос об оптимальности опорного плана решает следующая теорема: Теорема: если для некоторого плана 1. то план Отметим, что система (40.1) (m + n - 1) уравнений содержит (m + n) неизвестных Для «улучшения» опорного плана (при невыполнении условия (40.2)) выбирают свободную клетку с max ( Циклом называют замкнутую ломаную линию, все вершины которой лежат в занятых ячейках, кроме одной, расположенной в свободной клетке, подлежащей заполнению, а звенья параллельны строкам и столбцам, причем в каждой строке (столбце) лежит не более 2-х вершин. Всем вершинам поочередно приписывают знаки «+» и «-», начиная со свободной клетки.
где Новый опорный план снова проверяют на оптимальность с помощью системы уравнений потенциалов. Заметим, что в результате пересчета по циклу может оказаться число занятых клеток меньше, чем m+n-1 (план называется вырожденным). В этом случае следует заполнить числом «0» пустую клетку, имеющую минимальный тариф, и не образующую с занятыми клетками замкнутого прямоугольного контура. Свойство 1: если для некоторого оптимального плана
Пример: проверить оптимальность транспортную задачу, определенную таблицей: Таблица 40.1
Решение: Ведем построение опорного плана методом наименьшей стоимости. Таблица 40.2
Замечаем, что в результате пересчета по циклу оказалось, что число занятых клеток меньше, чем m + n - 1: Получаем опорный план: Вычислим общую сумму затрат на перевозку груза по этому плану:
Составляем систему уравнений потенциалов: Полагая Проверив свободные клетки, убеждаемся, что по теореме 5 план оптимален, следовательно, Данный оптимальный план не является единственным, так как для клетки А1В4 сумма потенциалов равна стоимости перевозки
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 793; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.141.201 (0.006 с.) |

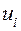 ,
,  и каждому пункту назначения
и каждому пункту назначения  - число
- число  ,
,  .
. ,
,  ,
,  транспортной задачи выполняются условия:
транспортной задачи выполняются условия: для
для  (для занятых клеток), (40.1)
(для занятых клеток), (40.1)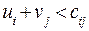 для
для 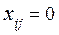 (для свободных клеток), (40.2)
(для свободных клеток), (40.2) является оптимальным.
является оптимальным. ,
,  , и потому, приравнивая одно из них, например
, и потому, приравнивая одно из них, например  ) и строят для нее цикл пересчета (сдвига).
) и строят для нее цикл пересчета (сдвига). , равной минимальному значению из всех чисел в отрицательных ячейках цикла. Во все положительные клетки прибавляется
, равной минимальному значению из всех чисел в отрицательных ячейках цикла. Во все положительные клетки прибавляется  , (40.3)
, (40.3) - сумма тарифов в положительных вершинах,
- сумма тарифов в положительных вершинах,  - в отрицательных вершинах цикла.
- в отрицательных вершинах цикла. ,
,  ,
,  для
для  (для свободных клеток), то существует как минимум еще один оптимальный план, для которого общая стоимость плана перевозок остается прежней, поскольку
(для свободных клеток), то существует как минимум еще один оптимальный план, для которого общая стоимость плана перевозок остается прежней, поскольку  .
.

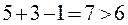 , т.е. получен вырожденный план. Следовательно, заполняем числом «0» пустую клетку А2В5 , т.к. она имеет минимальный тариф (
, т.е. получен вырожденный план. Следовательно, заполняем числом «0» пустую клетку А2В5 , т.к. она имеет минимальный тариф ( ), и не образует с занятыми клетками замкнутого прямоугольного контура.
), и не образует с занятыми клетками замкнутого прямоугольного контура.
 (ед.).
(ед.). ,
, , найдем:
, найдем:  ,
, 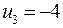 ,
, 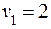 ,
,  ,
,  ,
,  ,
,  .
. .
. и в нее по циклу, можно переместить 10 ед. груза.
и в нее по циклу, можно переместить 10 ед. груза.


