Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача об использовании сырьяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для производства четырех видов изделий A1, A2, A3, A4 завод должен использовать три вида сырья I, II, III, запасы которого на планируемый период составляют соответственно 1000, 600 и 150 условных единиц. В приведенной ниже таблице даны технологические коэффициенты, т.е. расход каждого вида сырья на производство единицы каждого изделия и прибыль от реализации единицы изделия каждого вида. Таблица 34.2
Требуется составить такой план выпуска указанных изделий, чтобы обеспечить максимальную прибыль от их реализации. Составим математическую модель задачи: Обозначим через x1, x2, x3, x4 количество единиц соответствующих изделий: A1, A2, A3, A4. Тогда экономико-математическая модель задачи будет следующая: найти максимум функции
при выполнении системы ограничений
Для обращения системы ограничений-неравенств в систему уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные x5, x6, x7. Эти добавочные переменные в условиях данной задачи имеют конкретное экономическое содержание, а именно: объем остатков сырья каждого вида после выполнения плана выпуска продукции.
После введения добавочных переменных получим систему уравнений: Нужно найти такое допустимое базисное решение системы, которое бы максимизировало целевую функцию I шаг. Основные переменные x5, x6, x7. Условия нашей задачи выглядят следующим образом:
А целевая функция Составляем первую симплекс-таблицу. Так как ищем max, то выбираем наибольший отрицательный коэффициент функции Z. Таким образом, ключевым столбцом является столбец Таблица 34.3
Базисное решение (0; 0; 0; 0; 1000; 600; 150). II шаг. Основные переменные x1, x5, x6. Составляем новую симплекс-таблицу. Разрешающий элемент 1. Таблица 34.4
Умножим каждый элемент ключевой строки из таблицы 34.3 (исключая разрешающий элемент) на 1 и полученные значения запишем в строку с измененной базисной переменной. Таблица 34.5
Умножим каждый элемент ключевого столбца из таблицы 34.3 (исключая разрешающий элемент) на (-1)и полученные значения запишем в столбец с измененной свободной переменной. Таблица 34.6
Помня, что столбец, у которого в ключевой строке имеется 0, в новой таблице будет таким же и строка, у которой в ключевом столбце имеется 0, в новой таблице будет такой же, запишем. Таблица 34.7
Пользуясь схемой прямоугольника, заполняем таблицу. Таблица 34.8
Базисное решение (150; 0; 0; 0; 250; 0; 0). Так как во второй строке нашей новой таблицы есть отрицательный элемент, то полученное решение не оптимальное. Продолжаем искать оптимальное решение. Выбираем наибольший отрицательный коэффициент функции Z. Таким образом, ключевым столбцом является столбец Таблица 34.9
Б азисная переменная III шаг. Основные переменные x1, x2, x5. Составляем новую симплекс-таблицу. Разрешающий элемент 2. Заменяем разрешающий элемент на Таблица 34.10
Базисное решение (150; 0; 0; 0; 250; 0; 0). Так как во второй строке нашей новой таблицы есть отрицательный элемент, то полученное решение не оптимальное. Продолжаем искать оптимальное решение. Выбираем наибольший отрицательный коэффициент функции Z. Таким образом, ключевым столбцом является столбец Таблица 34.11
Б азисная переменная IV шаг. Основные переменные x2, x4, x5. Переходим к следующей таблице. Таблица 34.12
Так как во второй строке нашей новой таблицы нет отрицательных элементов, то полученное решение оптимальное. Эта таблица является последней, по ней читаем ответ задачи. Оптимальным будет решение (0; 225; 0; 150; 475; 0; 0) при котором Fmax =1050, т.е. для получения наибольшей прибыли, равной 1050 денежных единиц, предприятие должно выпустить 225 единиц продукции вида A2 , 150 единиц продукции вида A4 (продукцию вида A1 и A3 в данных условиях производить невыгодно); при этом сырье типа II и III будет использовано полностью, а 475 единиц сырья типа I останутся неизрасходованными.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.210.36 (0.007 с.) |


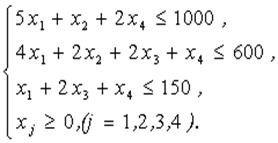
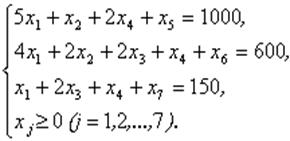
 , т.е. необходимо найти оптимальное решение задачи. Так как система ограничений состоит из трех независимых уравнений с семью переменными, то число основных (базисных) переменных должно равняться трем, а число не основных (свободных) — четырем.
, т.е. необходимо найти оптимальное решение задачи. Так как система ограничений состоит из трех независимых уравнений с семью переменными, то число основных (базисных) переменных должно равняться трем, а число не основных (свободных) — четырем.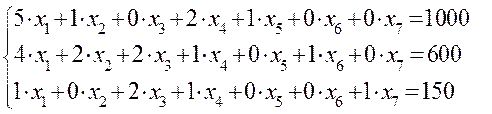
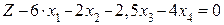
 . В этом столбце все базисные коэффициенты положительные,
. В этом столбце все базисные коэффициенты положительные, 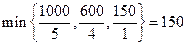 . Таким образом, ключевой строкой может быть
. Таким образом, ключевой строкой может быть  или
или 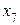 . Для удобства выбираем
. Для удобства выбираем 




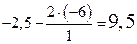
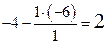


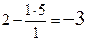


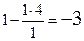
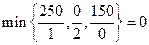 . Таким образом, ключевой строкой является
. Таким образом, ключевой строкой является 
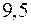


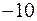
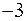


 ,
, 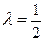 . Умножим каждый элемент ключевой строки из таблицы 34.9 (исключая разрешающий элемент) на
. Умножим каждый элемент ключевой строки из таблицы 34.9 (исключая разрешающий элемент) на 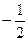 и полученные значения запишем в столбец с измененной свободной переменной. С толбец, у которого в ключевой строке имеется 0, в новой таблице будет таким же. С трока, у которой в ключевой строке имеется 0, в новой таблице будет такой же. Пользуясь схемой прямоугольника, заполняем таблицу.
и полученные значения запишем в столбец с измененной свободной переменной. С толбец, у которого в ключевой строке имеется 0, в новой таблице будет таким же. С трока, у которой в ключевой строке имеется 0, в новой таблице будет такой же. Пользуясь схемой прямоугольника, заполняем таблицу.