
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод искусственного базиса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Чтобы применить симплекс-метод для решения задачи ЛП в произвольной форме, необходимо выделить начальный допустимый базис. Для этого в симплекс-метод вводят подготовительный этап. Один из методов для реализации подготовительного этапа называется методом искусственного базиса. Алгоритм метода искусственного базиса. Шаг 1. Приводим задачу ЛП к каноническому виду с неотрицательными правыми частями
Шаг 2: Строим вспомогательную задачу ЛП
Переменные вспомогательной задачи Вспомогательная задача ЛП всегда имеет решение, причем оптимальное значение целевой функции Приводим вспомогательной задачи ЛП к специальному виду. Для этого целевую функцию выражаем через небазисные переменные.
Шаг 3: Решаем вспомогательную задачу ЛП симплекс-методом. Шаг 4: Если Шаг 5: Если Задача 35.1. Решить задачу линейного программирования
Заметим, что у нас уже есть одна базисная переменная
Итак, у нас получилась вспомогательная задача ЛП:
Исходная симплекс-таблица примет тогда вид:
Дальнейшие итерации приводятся без особых пояснений. Первая итерация Так как из базиса выводится вектор
Вторая итерация На этой итерации из базиса выводится вектор
Третья итерация Мы вернулись к исходной задаче и продолжаем решать ее по стандартной схеме.
Строка целевой функции не содержит положительных значений. Значит, задача решена и оптимальный план имеет вид: (0, 15/7, 25/7, 15/7) Двойственность задач линейного программирования. Таблица соответствий. Определение: двойственная задача – это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной задачи, которая в этом случае называется прямой задачей линейного программирования. Таблица 36.1
Трудности в решении задач линейного программирования зависят не от количества переменных n, а от количества ограничений m, определяющих число итераций симплекс-метода. Поэтому, если прямая задача линейного программирования, еще не приведенная к стандартной форме, содержит большое количество ограничений (m>n), то в этом случае целесообразно перейти к двойственной задаче. Сформированная двойственная задача линейного программирования будет иметь m переменных и n ограничений, т.е. количество итераций при этом уменьшится.
Рассмотрим пару задач ЛП вида: Таблица 36.2
Задачу (I) называют прямой задачей ЛП, а (II) - двойственной. Ограничения задач (I) и (II), соответствующие друг другу, называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую - двойственной. Грубо говоря, двойственная задача - это на 900 повернутая исходная прямая задача. В этой связи полезно усвоить следующую схему соответствия. Задача 36.1: построить двойственную задачу к следующей задаче ЛП:
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях задачи с целевой функцией. Так как целевая функция минимизируется, то неравенства должны быть записаны с помощью знака Теперь, вводя двойственные переменные
Таблица 36.3
Итак, задача слева - исходная прямая задача, задача справа - двойственная к исходной задаче.
Теоремы двойственности. Рассмотрим стандартную задачу ЛП и двойственную к ней: Таблица 37.1
Пара двойственных задач (I) и (II) называется парой симметрических двойственных задач. Не ограничивая общности, теорию двойственности можно рассматривать для пары симметрических задач, поскольку для любой задачи ЛП существует эквивалентная ей стандартная задача ЛП и поэтому теоремы, справедливые для пары симметрических двойственных задач, будут справедливы для пары общих двойственных задач. Рассмотрим пару симметрических двойственных задач в матричной форме записи. Таблица 37.2.
Здесь
Основное неравенство двойственности: для любых допустимых решений прямой задачи Следствие (достаточное условие оптимальности): если для некоторых допустимых решений Первая теорема двойственности: е сли одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают.
где Вторая теорема двойственности: чтобы допустимые решения 1) 2)
Критерии оптимальности. Первый критерий оптимальности: Решение
Второй критерий оптимальности: чтобы допустимые решения 1) если 2) если 3) если 4) если Пример: используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи.
Пусть решение задачи найдено одним из стандартных методов: Построим двойственную задачу:
По первой теореме двойственности задача разрешима, причем
Найдем оптимальный план задачи Получим
Следовательно, неравенство Далее, так как
Получаем систему линейных уравнений:
Планы
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1554; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.85.59 (0.012 с.) |

 ,
,  .
.
 (35.1)
(35.1)
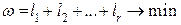
 (35.2)
(35.2) .
. образуют базис вспомогательной задачи ЛП и называются искусственными.
образуют базис вспомогательной задачи ЛП и называются искусственными.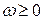
 (35.3)
(35.3) , то допустимого решения в исходной задаче не существует. Задача не разрешима и процесс решения исходной задачи завершается.
, то допустимого решения в исходной задаче не существует. Задача не разрешима и процесс решения исходной задачи завершается. , то приводим исходную задачу к виду (35.1) на основе оптимальной симплек-таблицы вспомогательной задачи ЛП. Подготовительный этап симплекс-метода исходной задачи на этом завершается.
, то приводим исходную задачу к виду (35.1) на основе оптимальной симплек-таблицы вспомогательной задачи ЛП. Подготовительный этап симплекс-метода исходной задачи на этом завершается.


 . Поэтому вводим лишь две искусственные переменные
. Поэтому вводим лишь две искусственные переменные  и
и  , заменяя исходную задачу следующей:
, заменяя исходную задачу следующей:








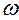






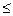 (этот знак неравенства согласован с целевой функцией на максимум)
(этот знак неравенства согласован с целевой функцией на максимум)

 , не имеющая ограничения в знаке
, не имеющая ограничения в знаке

 (этот знак неравенства согласован с целевой функцией на минимум)
(этот знак неравенства согласован с целевой функцией на минимум)
 , не имеющая ограничения в знаке
, не имеющая ограничения в знаке
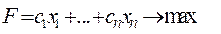
 ………………………
………………………
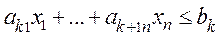



 ………
………

 - любое
……..
- любое
……..
 - любое
- любое

 ………
………
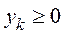
 - любое
……..
- любое
……..
 - любое
- любое
 ……………………………..
……………………………..
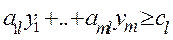





 Для этого второе неравенство умножим на -1:
Для этого второе неравенство умножим на -1: 
 ,
,  ,
,  , запишем в соответствии с указанным правилом пару двойственных задач:
, запишем в соответствии с указанным правилом пару двойственных задач:




 - любое
- любое
 - любое
- любое

 - любое
- любое







 ………………………
………………………




 ……………………………..
……………………………..







 ,
, 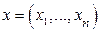 ,
, 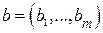 ,
,  ,
, - матрица из
- матрица из  строк и
строк и  столбцов,
столбцов,  - транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II).
- транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II). ,
, 
 и для любых допустимых решений двойственной задачи
и для любых допустимых решений двойственной задачи 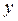 выполняется неравенство
выполняется неравенство  .
.  и
и  выполняется равенство значений целевых функций
выполняется равенство значений целевых функций  , то
, то  ,
,  - оптимальные решения задачи (I) и (II) соответственно.
- оптимальные решения задачи (I) и (II) соответственно. , (37.1)
, (37.1) ,
,  оптимальные планы задач (I) и (II) соответственно.
оптимальные планы задач (I) и (II) соответственно. ,
,  пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия:
пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия: , (37.2)
, (37.2) . (37.3)
. (37.3)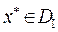 оптимально тогда и только тогда, когда существует решение
оптимально тогда и только тогда, когда существует решение  такое, что
такое, что . (38.1)
. (38.1) , то
, то 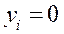 ; (38.2)
; (38.2) , то
, то  ; (38.3)
; (38.3) , то
, то  ; (38.4)
; (38.4)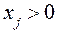 , то
, то  . (38.5)
. (38.5)
 , (38.6)
, (38.6) ,
,  ,
,  .
. ,
,  .
.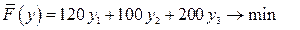
 , (38.7)
, (38.7) ,
,  ,
,  .
. .
. , используя вторую теорему двойственности. Подставим координаты вектора
, используя вторую теорему двойственности. Подставим координаты вектора  в ограничения задачи (38.6).
в ограничения задачи (38.6).


 должно выполняться как равенство, то есть
должно выполняться как равенство, то есть  .
. ,
,  , то
, то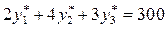 ,
,  .
. ,
,  ,
, 
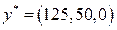 , в силу второй теоремы двойственности, являются оптимальными в задачах (38.6) и (38.7) соответственно.
, в силу второй теоремы двойственности, являются оптимальными в задачах (38.6) и (38.7) соответственно.


